This work is dedicated to Jim Wilkinson whose ideas and
spirit have given us inspiration and influenced the project
at every turn.
The printed version of LAPACK Users' Guide, Second Edition will be available
from SIAM in February 1995. The list price is $28.50 and the SIAM Member Price
is $22.80.Contact SIAM for additional information.
mail: SIAM, 3600 University City Science Center, Philadelphia, PA 19104-2688.
The royalties from the sales of this book are being placed in a fund
to help students attend SIAM meetings and other SIAM related activities.
This fund is administered by SIAM and qualified individuals are encouraged to
write directly to SIAM for guidelines.
Tue Nov 29 14:03:33 EST 1994
Contents




Next:
List of Tables
Up:
LAPACK Users' Guide Release
Previous:
LAPACK Users' Guide Release
Tue Nov 29 14:03:33 EST 1994
LAPACK Compared with LINPACK and EISPACK





Next:
LAPACK and the
Up:
Essentials
Previous:
Computers for which
LAPACK has been designed to supersede LINPACK
[26]
and EISPACK
[44]
[70]
, principally by restructuring the software to achieve much greater efficiency, where possible, on modern
high-performance computers; also by adding extra functionality,
by using some new or improved algorithms, and
by integrating the two sets
of algorithms into a unified package.
Appendix
D lists the LAPACK counterparts of LINPACK
and EISPACK routines. Not all the facilities of LINPACK and EISPACK are
covered by Release 2.0 of LAPACK.
Tue Nov 29 14:03:33 EST 1994
Design and Documentation of Argument Lists





Next:
Structure of the
Up:
Documentation and Software
Previous:
Documentation and Software
The argument lists of all LAPACK routines conform to a single
set of conventions for their design and documentation.
Specifications of all LAPACK driver and computational routines are given
in Part
2. These are derived from the specifications
given in the leading comments in the code, but in Part
2
the specifications for
real and complex versions of each routine have been merged, in order to
save space.
Tue Nov 29 14:03:33 EST 1994
Structure of the Documentation





Next:
Order of Arguments
Up:
Design and Documentation
Previous:
Design and Documentation
The documentation
of each LAPACK
routine includes:
- the SUBROUTINE or FUNCTION statement, followed by statements
declaring the type and dimensions of the arguments;
- a summary of the Purpose of the routine;
- descriptions of each of the Arguments in the order of
the argument list;
- (optionally) Further Details
(only in the code, not in Part
2);
- (optionally) Internal Parameters
(only in the code, not in Part
2).
Tue Nov 29 14:03:33 EST 1994
Order of Arguments





Next:
Argument Descriptions
Up:
Design and Documentation
Previous:
Structure of the
Arguments
of an LAPACK routine appear
in the following order:
- arguments specifying options;
- problem dimensions;
- array or scalar arguments defining the input data; some of them may be
overwritten by results;
- other array or scalar arguments returning results;
- work arrays (and associated array dimensions);
- diagnostic argument INFO.
Tue Nov 29 14:03:33 EST 1994
Argument Descriptions





Next:
Option Arguments
Up:
Design and Documentation
Previous:
Order of Arguments
The style of the argument
descriptions is illustrated by the following example:
- N
- (input) INTEGER
The number of columns of the matrix A. N > = 0.
- A
- (input/output) REAL array, dimension (LDA,N)
On entry, the m-by-n matrix to be factored.
On exit, the factors L and U from the factorization
A = P * L * U; the unit diagonal elements of L are not stored.
The description of each argument gives:
- a classification of the argument as (input), (output),
(input/output), (input or output)
 ,
(workspace) or (workspace/output)
,
(workspace) or (workspace/output)
 ;
;
- the type of the argument;
- (for an array) its dimension(s);
- a specification of the value(s) that must be supplied for the
argument (if it's an input argument), or of the value(s) returned
by the routine (if it's an output argument), or both (if it's an
input/output argument). In the last case, the two parts of the
description are introduced by the phrases ``On entry'' and
``On exit''.
- (for a scalar input argument) any constraints that the
supplied values must satisfy (such as ``N > = 0'' in the
example above).
Tue Nov 29 14:03:33 EST 1994
Option Arguments





Next:
Problem Dimensions
Up:
Design and Documentation
Previous:
Argument Descriptions
Arguments
specifying options are
usually of type CHARACTER*1.
The meaning of each valid value is given
, as in this
example:
- UPLO
- (input) CHARACTER*1
= 'U': Upper triangle of A is stored;
= 'L': Lower triangle of A is stored.
The corresponding lower-case characters
may be supplied (with the same meaning), but any other value is illegal
(see subsection
5.1.8).
A longer
character string can be passed as the actual argument, making the calling
program more readable, but only the first character is significant;
this is a standard feature of Fortran 77.
For example:
CALL SPOTRS('upper', . . . )
Tue Nov 29 14:03:33 EST 1994
Problem Dimensions





Next:
Array Arguments
Up:
Design and Documentation
Previous:
Option Arguments
It is permissible for the problem
dimensions
to be passed as zero, in
which case the computation (or part of it) is skipped.
Negative dimensions are regarded as erroneous.
Tue Nov 29 14:03:33 EST 1994
Array Arguments





Next:
Work Arrays
Up:
Design and Documentation
Previous:
Problem Dimensions
Each two-dimensional array argument
is
immediately followed in the
argument list by its leading dimension
, whose
name has the form LD<array-name>. For example:
- A
- (input/output) REAL/COMPLEX array, dimension (LDA,N)
... - LDA
- (input) INTEGER
The leading dimension of the array A. LDA > = max(1,M).
It should be assumed, unless stated otherwise, that vectors and
matrices are stored in one- and two-dimensional arrays in the
conventional manner. That is, if an array X of dimension (N) holds
a vector  , then X(i) holds
, then X(i) holds  for
for
i = 1,..., n.
If a two-dimensional array A of dimension (LDA,N) holds an m-by-n
matrix A,
then A(i,j) holds  for i = 1,..., m and
j = 1,..., n (LDA must be at least m).
See Section
5.3 for more about
storage of matrices.
for i = 1,..., m and
j = 1,..., n (LDA must be at least m).
See Section
5.3 for more about
storage of matrices.
Note that
array arguments are usually declared in the software as assumed-size arrays
(last dimension *), for example:
REAL A( LDA, * )
although the documentation gives the dimensions as (LDA,N). The latter
form is more informative since it specifies the required minimum value of
the last dimension. However
an assumed-size array declaration has been used in the software,
in order to overcome some
limitations in the Fortran 77 standard. In particular it allows the
routine to be called when the relevant dimension (N, in this case) is zero.
However actual array dimensions in the calling program must be at
least 1 (LDA in this example).
Tue Nov 29 14:03:33 EST 1994
Work Arrays





Next:
Error Handling and
Up:
Design and Documentation
Previous:
Array Arguments
Many LAPACK routines require one or more work
arrays
to be passed as
arguments. The name of a work array is usually WORK - sometimes
IWORK, RWORK or BWORK to distinguish work arrays of
integer, real or logical (Boolean) type.
Occasionally the first element of a work array is used to return some
useful information: in such cases, the argument is described as
(workspace/output) instead of simply (workspace).
A number of routines implementing block algorithms require workspace
sufficient to hold one block of rows or columns of the matrix,
for example, workspace
of size n-by-nb, where nb is the block size.
In such cases, the actual declared length of the work array
must be passed as a separate argument LWORK
,
which immediately follows WORK in the argument-list.
See Section
5.2 for further explanation.
Tue Nov 29 14:03:33 EST 1994
Error Handling and the Diagnostic Argument INFO





Next:
Determining the Block
Up:
Design and Documentation
Previous:
Work Arrays
All
documented routines
have a
diagnostic argument INFO
that
indicates the success or failure of the computation, as follows:
- INFO = 0: successful termination
- INFO < 0: illegal value of one or more arguments - no computation
performed
- INFO > 0: failure in the course of computation
All driver and auxiliary routines
check that input arguments such as N or LDA or
option arguments of type character
have permitted values.
If an illegal value of the i-th argument is detected, the routine
sets INFO = -i, and then calls an error-handling routine XERBLA.
The standard version of XERBLA issues an error message and halts execution,
so that no LAPACK routine would ever return to the calling program with
INFO < 0. However, this might occur if a non-standard version of XERBLA
is used.
Tue Nov 29 14:03:33 EST 1994
Determining the Block Size for Block Algorithms





Next:
Matrix Storage Schemes
Up:
Documentation and Software
Previous:
Error Handling and
LAPACK routines that implement block algorithms need to determine
what block size
to use.
The intention behind the design of LAPACK is that the choice of block size
should be hidden from users as much as possible, but at the same time
easily accessible to installers of the package
when tuning LAPACK for a particular machine.
LAPACK routines call an auxiliary enquiry function ILAENV
, which returns
the optimal block size to be used, as well as other parameters.
The version of ILAENV
supplied with the
package contains
default values that led to good behavior over a reasonable
number of our test machines, but to achieve optimal
performance, it may be beneficial to
tune ILAENV
for your
particular machine environment.
Ideally a distinct implementation of ILAENV is needed for each
machine environment (see also Chapter
6).
The optimal block size may also depend on the routine, the combination of
option arguments (if any), and the problem dimensions.
If ILAENV
returns a block size
of 1, then the routine performs the unblocked algorithm, calling Level 2 BLAS,
and makes no calls to Level 3 BLAS.
Some LAPACK routines require a work array whose size is proportional to
the block size (see subsection
5.1.7). The actual length
of the work array is supplied as an argument LWORK. The description of
the arguments WORK and LWORK typically goes as follows:
- WORK
- (workspace) REAL array, dimension (LWORK)
On exit, if INFO = 0, then WORK(1) returns the optimal LWORK.
- LWORK
- (input) INTEGER
The dimension of the array WORK. LWORK  max(1,N).
max(1,N).
For optimal performance LWORK  N*NB,
where NB is the optimal block size returned by ILAENV.
N*NB,
where NB is the optimal block size returned by ILAENV.
The routine determines the block size to be used by the following steps:
- the optimal block size is determined by calling ILAENV;
- if the value of LWORK indicates that enough workspace has been
supplied, the routine uses the optimal block size;
- otherwise, the routine determines the largest block size that
can be used with the supplied amount of workspace;
- if this new block size does not fall below a
threshold value (also returned by ILAENV), the routine uses the new
value;
- otherwise, the routine uses the unblocked algorithm.
The minimum value of LWORK that would be needed to use
the optimal block size, is returned in WORK(1).
Thus, the routine uses the largest block size allowed by the amount
of workspace supplied, as long as this is likely to
give better performance than the unblocked algorithm.
WORK(1) is not always a simple formula in terms of N and NB.
The specification of LWORK gives the minimum value for the
routine to return correct results. If the supplied value is less than
the minimum - indicating that there is insufficient workspace to perform
the unblocked algorithm - the value of LWORK is regarded as an illegal value,
and is treated like any other illegal argument value
(see subsection
5.1.8).
If in doubt about how much workspace to supply, users should supply a generous
amount (assume a block size of 64, say),
and then examine the value of WORK(1) on exit.





Next:
Matrix Storage Schemes
Up:
Documentation and Software
Previous:
Error Handling and
Tue Nov 29 14:03:33 EST 1994
LAPACK and the BLAS





Next:
Documentation for LAPACK
Up:
Essentials
Previous:
LAPACK Compared with
LAPACK routines are written so that as much as possible of the
computation is performed by calls to the
Basic Linear Algebra Subprograms (BLAS)
[28]
[30]
[58]
.
Highly efficient machine-specific implementations of the BLAS are
available for many modern high-performance computers. The BLAS
enable LAPACK routines to achieve high performance with portable code.
The methodology for
constructing LAPACK routines in terms of calls to the BLAS
is described in Chapter
3.
The BLAS are not strictly speaking part of LAPACK, but Fortran 77 code
for the BLAS is distributed with LAPACK, or can be obtained separately
from netlib (see below). This code constitutes the
``model implementation''
[27]
[29].
The model implementation is not expected
to perform as well as a specially tuned implementation
on most high-performance computers - on some machines it may give much
worse performance - but it
allows users to run LAPACK codes on machines that do not offer any other
implementation of the BLAS.
Tue Nov 29 14:03:33 EST 1994
Matrix Storage Schemes





Next:
Conventional Storage
Up:
Documentation and Software
Previous:
Determining the Block
LAPACK allows the following different storage schemes
for matrices:
- conventional storage in a two-dimensional array;
- packed storage for symmetric, Hermitian or triangular matrices;
- band storage for band matrices;
- the use of two or three
one-dimensional arrays to store tridiagonal or bidiagonal
matrices.
These storage schemes are compatible with those
used in LINPACK
and the BLAS, but EISPACK
uses incompatible schemes
for band and tridiagonal matrices.
In the examples below,  indicates an array element that need not be set
and is not referenced by LAPACK routines. Elements that ``need not be
set'' are never read, written to, or otherwise accessed by the LAPACK
routines. The examples illustrate only the
relevant part of the arrays; array arguments may of course have additional
rows or columns, according to the usual rules for passing array arguments
in Fortran 77.
indicates an array element that need not be set
and is not referenced by LAPACK routines. Elements that ``need not be
set'' are never read, written to, or otherwise accessed by the LAPACK
routines. The examples illustrate only the
relevant part of the arrays; array arguments may of course have additional
rows or columns, according to the usual rules for passing array arguments
in Fortran 77.
Tue Nov 29 14:03:33 EST 1994
Conventional Storage





Next:
Packed Storage
Up:
Matrix Storage Schemes
Previous:
Matrix Storage Schemes
The default scheme for storing matrices
is the obvious one described in subsection
5.1.6:
a matrix A is stored in a two-dimensional array A, with
matrix element  stored in array element A(i,j).
stored in array element A(i,j).
If a matrix is triangular
(upper or lower, as specified by
the argument UPLO), only the elements of the relevant triangle
are accessed. The remaining elements of the array need not be set.
Such elements are indicated by * in the examples below.
For example, when n = 4:

Similarly, if the matrix is upper Hessenberg, elements below the
first subdiagonal need not be set.
Routines that handle symmetric
or Hermitian
matrices
allow for either the upper or lower triangle of the matrix
(as specified by UPLO) to
be stored in the corresponding elements of the array; the remaining
elements of the array need not be set.
For example, when n = 4:

Tue Nov 29 14:03:33 EST 1994
Packed Storage





Next:
Band Storage
Up:
Matrix Storage Schemes
Previous:
Conventional Storage
Symmetric, Hermitian or triangular matrices may be stored more
compactly
, if the relevant
triangle (again as specified by UPLO) is packed
by columns in a one-dimensional array. In LAPACK, arrays that hold
matrices in packed storage, have names ending in `P'. So:
- if UPLO = `U',
 is stored in AP(i + j(j - 1)/2) for i < = j;
is stored in AP(i + j(j - 1)/2) for i < = j;
- if UPLO = `L',
 is stored in
AP(i + (2n - j)(j - 1)/2) for
j < = i.
is stored in
AP(i + (2n - j)(j - 1)/2) for
j < = i.
For example:

Note that for real or complex symmetric matrices,
packing the upper triangle
by columns is equivalent to packing the lower triangle by rows;
packing the lower triangle by columns is equivalent to packing
the upper triangle by rows.
For complex Hermitian matrices,
packing the upper triangle
by columns is equivalent to packing the conjugate of the lower triangle by rows;
packing the lower triangle by columns is equivalent to packing
the conjugate of the upper triangle by rows.
Tue Nov 29 14:03:33 EST 1994
Band Storage





Next:
Tridiagonal and Bidiagonal
Up:
Matrix Storage Schemes
Previous:
Packed Storage
An m-by-n band matrix
with kl subdiagonals
and ku superdiagonals may be
stored compactly in a two-dimensional array with kl + ku + 1 rows and n columns.
Columns of the matrix are stored in corresponding columns of the
array, and diagonals of the matrix are stored in rows of the array.
This storage scheme should be used in practice only if kl , ku << min(m , n),
although LAPACK routines work correctly for all values of kl and ku.
In LAPACK, arrays that hold matrices in band storage have names
ending in `B'.
To be precise,  is stored in AB(ku + 1 + i - j , j) for
max(1 , j - ku) < = i < = min(m , j + kl).
For example, when m = n = 5, kl = 2 and ku = 1:
is stored in AB(ku + 1 + i - j , j) for
max(1 , j - ku) < = i < = min(m , j + kl).
For example, when m = n = 5, kl = 2 and ku = 1:

The elements marked * in the upper left and lower right
corners of the array AB need not be set, and are not referenced by
LAPACK routines.
Note: when a band matrix is supplied for LU factorization,
space
must be allowed to store an
additional kl superdiagonals,
generated by fill-in as a result of row interchanges.
This means that the matrix is stored according to the above scheme,
but with kl + ku superdiagonals.
Triangular band matrices are stored in the same format, with either
kl = 0 if upper triangular, or ku = 0 if
lower triangular.
For symmetric or Hermitian band matrices with kd subdiagonals or
superdiagonals, only the upper or lower triangle (as specified by
UPLO) need be stored:
- if UPLO = `U',
 is stored in AB(kd + 1 + i - j , j) for
is stored in AB(kd + 1 + i - j , j) for
max(1 , j - kd) < = i < = j;
- if UPLO = `L',
 is stored in AB(1 + i - j , j) for
j < = i < = min(n , j + kd).
is stored in AB(1 + i - j , j) for
j < = i < = min(n , j + kd).
For example, when n = 5 and kd = 2:

EISPACK
routines use a different storage scheme for band matrices,
in which rows of the matrix are stored in corresponding rows of the
array, and diagonals of the matrix are stored in columns of the array
(see Appendix
D).
Tue Nov 29 14:03:33 EST 1994
Tridiagonal and Bidiagonal Matrices





Next:
Unit Triangular Matrices
Up:
Matrix Storage Schemes
Previous:
Band Storage
An unsymmetric
tridiagonal matrix of order n is stored in
three one-dimensional arrays, one of length n containing the
diagonal elements, and two of length n - 1 containing the
subdiagonal and superdiagonal elements in elements 1 : n - 1.
A symmetric
tridiagonal or
bidiagonal
matrix is stored in
two one-dimensional arrays, one of length n containing the
diagonal elements, and one of length n containing the
off-diagonal elements. (EISPACK routines store the off-diagonal
elements in elements 2 : n of a vector of length n.)
Tue Nov 29 14:03:33 EST 1994
Unit Triangular Matrices





Next:
Real Diagonal Elements
Up:
Matrix Storage Schemes
Previous:
Tridiagonal and Bidiagonal
Some LAPACK routines have an option to handle unit triangular matrices
(that is, triangular matrices with diagonal elements = 1). This option
is specified by an argument DIAG
. If DIAG = 'U' (Unit triangular),
the diagonal elements of the matrix need not be stored, and the
corresponding array elements are not referenced by the LAPACK routines.
The storage scheme for the rest of the matrix (whether conventional,
packed or band) remains unchanged, as described in
subsections
5.3.1,
5.3.2 and
5.3.3.
Tue Nov 29 14:03:33 EST 1994
Real Diagonal Elements of Complex Matrices





Next:
Representation of Orthogonal
Up:
Matrix Storage Schemes
Previous:
Unit Triangular Matrices
Complex Hermitian
matrices
have diagonal matrices that are by definition
purely real. In addition, some complex triangular matrices computed by
LAPACK routines are defined by the algorithm to have real diagonal elements
- in Cholesky or QR factorization, for example.
If such matrices are supplied as input to LAPACK routines,
the imaginary parts of the diagonal elements are not referenced,
but are assumed to be zero. If such matrices are returned as output by LAPACK
routines, the computed imaginary parts are explicitly set to zero.
Tue Nov 29 14:03:33 EST 1994
Representation of Orthogonal or Unitary Matrices





Next:
Installing LAPACK Routines
Up:
Documentation and Software
Previous:
Real Diagonal Elements
A real orthogonal or complex unitary matrix (usually denoted Q) is often
represented
in
LAPACK as a product of elementary reflectors - also referred to as
elementary Householder matrices (usually denoted  ). For example,
). For example,

Most users need not be aware
of the details, because LAPACK routines are provided to work with this
representation:
- routines whose names begin SORG- (real) or CUNG- (complex) can generate
all or part of Q explicitly;
- routines whose name begin SORM- (real) or CUNM- (complex) can multiply
a given matrix by Q or
 without forming Q explicitly.
without forming Q explicitly.
The following further details may occasionally be useful.
An elementary reflector (or elementary Householder matrix) H of order
n is a
unitary matrix
of the form

where  is a scalar, and v is an n-vector, with
is a scalar, and v is an n-vector, with
 ); v is often referred to
as the Householder vector
.
Often v has several leading or trailing zero elements, but for the
purpose of this discussion assume that H has no such special structure.
); v is often referred to
as the Householder vector
.
Often v has several leading or trailing zero elements, but for the
purpose of this discussion assume that H has no such special structure.
There is some redundancy in the representation (
5.1), which can be
removed in
various ways. The representation used in LAPACK (which differs from
those used in LINPACK or EISPACK) sets  ; hence
; hence  need not
be stored. In real arithmetic,
need not
be stored. In real arithmetic,  , except that
, except that
 implies H = I.
implies H = I.
In complex arithmetic
,  may be
complex, and satisfies
may be
complex, and satisfies
 and
and  .
Thus a complex H is
not Hermitian (as it is in other representations), but it is unitary,
which is the important property. The advantage of allowing
.
Thus a complex H is
not Hermitian (as it is in other representations), but it is unitary,
which is the important property. The advantage of allowing  to be
complex is that, given an arbitrary complex vector x, H can be computed
so that
to be
complex is that, given an arbitrary complex vector x, H can be computed
so that

with real  . This is useful, for example,
when reducing a complex Hermitian matrix to real symmetric tridiagonal form
,
or a complex rectangular matrix to real bidiagonal form
.
. This is useful, for example,
when reducing a complex Hermitian matrix to real symmetric tridiagonal form
,
or a complex rectangular matrix to real bidiagonal form
.
For further details, see Lehoucq
[59].





Next:
Installing LAPACK Routines
Up:
Documentation and Software
Previous:
Real Diagonal Elements
Tue Nov 29 14:03:33 EST 1994
Installing LAPACK Routines





Next:
Points to Note
Up:
Guide
Previous:
Representation of Orthogonal
Tue Nov 29 14:03:33 EST 1994
Points to Note





Next:
Installing ILAENV
Up:
Installing LAPACK Routines
Previous:
Installing LAPACK Routines
For anyone who obtains the complete LAPACK package from netlib
or NAG (see Chapter
1), a
comprehensive installation
guide
is provided. We recommend
installation of the complete package as the most convenient and reliable
way to make LAPACK available.
People who obtain copies of a few LAPACK routines from netlib need to be
aware of the following points:
- Double precision complex routines (names beginning Z-)
use a COMPLEX*16 data type. This is an extension to the Fortran 77
standard, but is provided by many Fortran compilers on machines
where double precision computation is usual.
The following related extensions are also used:
- the intrinsic function DCONJG, with argument and result of type
COMPLEX*16;
- the intrinsic functions DBLE and DIMAG, with COMPLEX*16 argument
and DOUBLE PRECISION result, returning the real and imaginary parts,
respectively;
- the intrinsic function DCMPLX, with DOUBLE PRECISION argument(s)
and COMPLEX*16 result;
- COMPLEX*16 constants, formed from a pair of double precision
constants in parentheses.
Some compilers provide DOUBLE COMPLEX as an alternative to COMPLEX*16,
and an intrinsic function DREAL instead of DBLE to return the
real part of a COMPLEX*16 argument.
If the compiler does not accept the constructs used in LAPACK, the installer
will have to modify the code: for example, globally change COMPLEX*16 to
DOUBLE COMPLEX, or selectively change DBLE to DREAL.

-
For optimal performance, a small set of tuning parameters must be set
for each machine, or even for each configuration of a given machine
(for example, different parameters may be optimal for different numbers
of processors).
These values
, such as the block size, minimum block size, crossover
point below which an unblocked routine should be used, and others,
are set by calls to an inquiry function ILAENV.
The default version of ILAENV
provided with LAPACK uses generic values
which often give satisfactory performance, but
users who are particularly interested in performance may wish to
modify this subprogram or substitute their own version.
Further details on setting ILAENV for a particular environment
are provided in section
6.2.
-
SLAMCH/DLAMCH
determines properties of the
floating-point arithmetic at run-time, such as the machine epsilon,
underflow threshold,
overflow threshold, and related parameters. It works satisfactorily on
all commercially important machines of which we are aware, but will necessarily
be updated from time to time as new machines and compilers are produced.





Next:
Installing ILAENV
Up:
Installing LAPACK Routines
Previous:
Installing LAPACK Routines
Tue Nov 29 14:03:33 EST 1994
Documentation for LAPACK





Next:
Availability of LAPACK
Up:
Essentials
Previous:
LAPACK and the
This Users' Guide gives an informal introduction to
the design of the package, and a detailed description of its contents.
Chapter
5 explains the conventions used in the
software and documentation.
Part
2 contains complete specifications of all the
driver routines and computational routines. These specifications have been
derived from the leading comments in the source text.
On-line manpages (troff files) for LAPACK routines, as well as for most of
the BLAS routines, are available on netlib. These files are
automatically generated at the time of each release. For more
information, see the manpages.tar.z entry on the lapack
index on netlib.
Tue Nov 29 14:03:33 EST 1994
Installing ILAENV





Next:
Troubleshooting
Up:
Installing LAPACK Routines
Previous:
Points to Note
Machine-dependent
parameters
such as the block size are set
by calls to an inquiry function which may be set with different
values on each machine.
The declaration of the environment inquiry function is
INTEGER FUNCTION ILAENV( ISPEC, NAME, OPTS, N1, N2, N3, N4 )
where ISPEC, N1, N2, N3, and N4 are integer variables and
NAME and OPTS are CHARACTER*(*). NAME specifies the subroutine name:
OPTS is a character string of options to the subroutine; and N1-N4 are
the problem dimensions.
ISPEC specifies the parameter to be returned; the following values are
currently used in LAPACK:
ISPEC = 1: NB, optimal block size
= 2: NBMIN, minimum block size for the block routine
to be used
= 3: NX, crossover point (in a block routine, for
N < NX, an un blocked routine should be used)
= 4: NS, number of shifts
= 6: NXSVD is the threshold point for which the QR
factorization is performed prior to reduction to
bidiagonal form. If M > NXSVD * N, then a
QR factorization is performed.
= 8: MAXB, crossover point for block multishift QR
The three block size parameters, NB, NBMIN, and NX, are used in many
different
subroutines (see Table
6.1).
NS and MAXB are used
in the
block multishift QR algorithm, xHSEQR.
NXSVD is used
in the driver
routines xGELSS and xGESVD.

Table 6.1: Use of the block parameters NB, NBMIN, and NX in LAPACK
The LAPACK testing and timing programs use a special version of ILAENV
where the parameters are set via a COMMON block interface.
This is convenient for experimenting with different values of, say,
the block size in order to exercise different parts of the code
and to compare the relative performance of different parameter values.
The LAPACK timing programs were designed to collect data for all the
routines in Table
6.1.
The range of problem sizes needed to determine the optimal block size
or crossover point
is machine-dependent, but the
input files
provided with the LAPACK test and timing package can be used as a
starting point.
For subroutines that require a crossover point, it is best to start by
finding the best block size
with the crossover
point set to 0, and then
to locate the point at which the performance of the unblocked algorithm
is beaten by the block algorithm.
The best crossover point
will be somewhat smaller than the point
where the curves for the unblocked and blocked methods cross.
For example, for SGEQRF
on a single processor of a CRAY-2,
NB = 32 was observed to be a good block size
,
and the performance of the block algorithm with this block size
surpasses the unblocked algorithm for square matrices
between N = 176 and N = 192.
Experiments with crossover points from 64 to 192 found that NX = 128
was a good choice, although the results for NX from 3*NB to 5*NB
are broadly similar.
This means that matrices with N < = 128 should use the unblocked
algorithm, and for N > 128 block updates should be used until the
remaining submatrix has order less than 128.
The performance of the unblocked (NB = 1) and blocked (NB = 32)
algorithms for SGEQRF
and for the blocked algorithm with a crossover
point of 128 are compared in Figure
6.1.

Figure 6.1: QR factorization on CRAY-2 (1 processor)
By experimenting with small values of the block size,
it should be straightforward to choose NBMIN,
the smallest block size that gives a performance improvement
over the unblocked algorithm.
Note that on some machines, the optimal block size may be 1
(the unblocked algorithm gives the best performance);
in this case, the choice of NBMIN is arbitrary.
The prototype version of ILAENV
sets NBMIN to 2, so that blocking
is always done, even though this could lead to poor performance
from a block routine if insufficient workspace is supplied
(see chapter
7).
Complicating the determination of optimal parameters is the fact that
the orthogonal factorization routines and SGEBRD
accept non-square
matrices as input.
The LAPACK timing program allows M and N to be varied independently.
We have found the optimal block size to be
generally insensitive to the shape of the matrix,
but the crossover point is more dependent on the matrix shape.
For example, if
M >> N in the QR factorization, block updates
may always be faster than unblocked updates on the remaining submatrix,
so one might set NX = NB if M > = 2N.
Parameter values for the number of shifts, etc.
used to tune the block multishift QR
algorithm
can be varied from the input files to the eigenvalue timing program.
In particular, the performance of xHSEQR is particularly sensitive to
the correct choice of block parameters. Setting NS = 2 will give
essentially the same performance as EISPACK
.
Interested users should consult
[3] for a description of
the timing program input files.





Next:
Troubleshooting
Up:
Installing LAPACK Routines
Previous:
Points to Note
Tue Nov 29 14:03:33 EST 1994
Troubleshooting





Next:
Common Errors in
Up:
Guide
Previous:
Installing ILAENV
Tue Nov 29 14:03:33 EST 1994
Common Errors in Calling LAPACK Routines





Next:
Failures Detected by
Up:
Troubleshooting
Previous:
Troubleshooting
For the benefit of less experienced programmers, we give here a list of
common programming errors in calling an LAPACK routine.
These errors may cause the LAPACK routine to report a failure,
as described in Section
7.2
;
they may cause an error to be reported by the system;
or they may lead to wrong results - see also
Section
7.3.
- wrong number of arguments
- arguments in the wrong order
- an argument of the wrong type (especially real and complex
arguments of the wrong precision)
- wrong dimensions for an array argument
- insufficient space in a workspace argument
- failure to assign a value to an input argument
Some modern compilation systems, as well as
software tools such as the portability checker in
Toolpack
[66], can check that arguments agree in number and type;
and many compilation systems offer run-time detection
of errors such as an array element out-of-bounds or use of an
unassigned variable.
Tue Nov 29 14:03:33 EST 1994
Failures Detected by LAPACK Routines





Next:
Invalid Arguments and
Up:
Troubleshooting
Previous:
Common Errors in
There are two ways in which an LAPACK routine may report a failure to
complete a computation successfully.
Tue Nov 29 14:03:33 EST 1994
Invalid Arguments and XERBLA





Next:
Computational Failures and
Up:
Failures Detected by
Previous:
Failures Detected by
If an illegal value is supplied for one of the input arguments to
an LAPACK routine, it will call the error handler XERBLA to write
a message to the standard output unit of the form:
** On entry to SGESV parameter number 4 had an illegal value
This particular message would be caused by passing to SGESV
a value of LDA
which was less than the value of the argument N.
The documentation for SGESV
in Part
2 states the set of acceptable input values:
``LDA > = max(1,N).'' This is required in order that the
array A with leading dimension LDA can store an n-by-n
matrix.
 The arguments are checked in order, beginning with the first.
In the above example, it may - from the user's point of view - be the
value of N which is in fact wrong.
Invalid arguments are often caused by the kind of error listed in
Section
7.1.
The arguments are checked in order, beginning with the first.
In the above example, it may - from the user's point of view - be the
value of N which is in fact wrong.
Invalid arguments are often caused by the kind of error listed in
Section
7.1.
In the model implementation of XERBLA
which is supplied with LAPACK,
execution stops after the
message; but the call to XERBLA is followed by a RETURN statement
in the LAPACK routine, so that if the installer removes the
STOP statement in XERBLA, the result will be an immediate exit from the
LAPACK routine with a negative value of INFO.
It is good practice always to check for a non-zero value of INFO
on return from an LAPACK routine.
(We recommend however that XERBLA should not be modified to return control
to the calling routine, unless absolutely
necessary, since this would remove one of the built-in safety-features
of LAPACK.)
Tue Nov 29 14:03:33 EST 1994
Computational Failures and INFO > 0





Next:
Wrong Results
Up:
Failures Detected by
Previous:
Invalid Arguments and
A positive value of INFO on return from an LAPACK routine indicates a
failure in the course of the algorithm. Common causes are:
- a matrix is singular (to working precision);
- a symmetric matrix is not positive definite;
- an iterative algorithm for computing eigenvalues or eigenvectors
fails to converge in the permitted number of iterations.
For example, if SGESVX
is called to solve a system of equations
with a coefficient matrix that is approximately singular,
it may detect exact singularity at the i-th stage of the LU
factorization, in which case it returns INFO = i;
or (more probably) it may compute an estimate of the reciprocal condition number
that is less than machine precision, in which case it returns INFO = n + 1.
Again, the documentation in Part
2 should be consulted for a
description of the error.
When a failure with INFO > 0 occurs, control is always returned
to the calling program; XERBLA is not called, and no error message
is written.
It is worth repeating that it is good practice always to check for
a non-zero value of INFO on return from an LAPACK routine.
A failure with INFO > 0 may indicate any of the following:
- an inappropriate routine was used:
for example, if a routine fails because a symmetric matrix turns out not to be
positive definite, consider using a routine for symmetric indefinite matrices.
- a single precision routine was used when double precision was needed:
for example, if SGESVX
reports approximate singularity
(as illustrated above), the corresponding double precision routine DGESVX
may be able to solve the problem (but nevertheless the problem is
ill-conditioned).
- a programming error occurred in generating the data supplied
to a routine: for example, even though theoretically a matrix should be
well-conditioned and positive-definite, a programming error in generating
the matrix could easily destroy either of those properties.
- a programming error occurred in calling the routine, of the kind
listed in Section
7.1.





Next:
Wrong Results
Up:
Failures Detected by
Previous:
Invalid Arguments and
Tue Nov 29 14:03:33 EST 1994
Wrong Results





Next:
Poor Performance
Up:
Troubleshooting
Previous:
Computational Failures and
Wrong results from LAPACK routines are most often caused by incorrect usage.
It is also possible that wrong results are caused by a bug
outside of LAPACK, in the compiler or in one of the library routines,
such as the BLAS, that are linked with LAPACK.
Test procedures are available for both LAPACK and the BLAS, and
the LAPACK installation guide
[3] should be consulted
for descriptions of the tests and for advice on resolving problems.
A list of known problems, compiler errors, and bugs in LAPACK routines is
maintained on netlib; see Chapter
1.
Users who suspect they have found a new bug in an LAPACK routine are
encouraged to report it promptly to the developers as directed in
Chapter
1.
The bug report should include a test case, a description of
the problem and expected results, and the actions, if any,
that the user has already taken to fix the bug.
Tue Nov 29 14:03:33 EST 1994
Poor Performance





Next:
Index of Driver
Up:
Troubleshooting
Previous:
Wrong Results
We have tried to make
the performance of LAPACK ``transportable'' by performing most of
the computation within the Level 1, 2, and 3 BLAS, and by isolating
all of the machine-dependent tuning parameters
in a single integer function ILAENV
.
To avoid poor performance
from LAPACK
routines, note the
following recommendations
:
- BLAS:
-
One should use BLAS that have been optimized for the machine being used
if they are available.
Many manufacturers and research institutions have developed, or are
developing, efficient versions of the BLAS for particular machines.
A portable set of Fortran BLAS is supplied with LAPACK
and can always be used if no other BLAS are available or if
there is a suspected problem in the local BLAS library, but
no attempt has been made to structure the Fortran BLAS for
high performance.
- ILAENV:
- For best performance, the LAPACK routine ILAENV
should be set with optimal tuning parameters for the machine being used.
The version of ILAENV provided with LAPACK supplies default values
for these parameters that give good, but not optimal, average
case performance on a range of existing machines.
In particular, the performance of xHSEQR is particularly sensitive to
the correct choice of block parameters; the same applies to the driver
routines which call xHSEQR, namely xGEES, xGEESX, xGEEV and xGEEVX.
Further details on setting parameters in ILAENV are found in
section
6.
- LWORK
 WORK(1):
WORK(1):
-
The performance of some routines depends on the amount of workspace
supplied. In such cases,
an argument, usually called WORK, is
provided, accompanied by an integer argument LWORK specifying its
length as a linear array.
On exit, WORK(1) returns the amount of workspace required to use
the optimal tuning parameters.
If LWORK < WORK(1), then insufficient workspace was provided
to use the optimal parameters, and the performance may be less
than possible.
One should check that LWORK
 WORK(1) on return from
an LAPACK routine requiring user-supplied workspace to see if
enough workspace has been provided.
Note that the computation is performed correctly, even if the amount of
workspace is less than optimal, unless LWORK is reported as an
invalid value by a call to XERBLA as described in Section
7.2.
WORK(1) on return from
an LAPACK routine requiring user-supplied workspace to see if
enough workspace has been provided.
Note that the computation is performed correctly, even if the amount of
workspace is less than optimal, unless LWORK is reported as an
invalid value by a call to XERBLA as described in Section
7.2.
- xLAMCH:
- Users should beware of the high cost of the first
call to the LAPACK auxiliary routine xLAMCH,
which computes
machine characteristics such as epsilon and the
smallest invertible number.
The first call dynamically determines a set of parameters defining
the machine's arithmetic, but these values are saved and subsequent
calls incur only a trivial cost.
For performance testing, the initial cost can be hidden by
including a call to xLAMCH in the main program, before any calls to
LAPACK routines that will be timed. A sample use of SLAMCH
is
XXXXXX = SLAMCH( 'P' )
or in double precision:
XXXXXX = DLAMCH( 'P' )
A cleaner but less portable solution is for the installer to
save the values computed by xLAMCH for a specific machine
and create a new version of xLAMCH with these constants set in
DATA statements, taking care that no accuracy is lost in the
translation.





Next:
Index of Driver
Up:
Troubleshooting
Previous:
Wrong Results
Tue Nov 29 14:03:33 EST 1994
Index of Driver and Computational Routines





Next:
Notes
Up:
Guide
Previous:
Poor Performance
Tue Nov 29 14:03:33 EST 1994
Notes





Next:
Index of Auxiliary
Up:
Index of Driver
Previous:
Index of Driver
- This index
lists related pairs of real and complex routines together,
for example, SBDSQR and CBDSQR.
- Driver routines are listed in bold type, for example SGBSV and
CGBSV.
- Routines are listed in alphanumeric order
of the real (single precision) routine name (which always begins with S-).
(See subsection
2.1.3 for details of the LAPACK naming scheme.)
- Double precision routines are not listed here;
they have names beginning with D- instead of
S-, or Z- instead of C-.
- This index gives only a brief description of the purpose of each
routine. For a precise description, consult the specifications
in Part
2, where the routines appear in the same
order as here.
- The text of the descriptions applies to both real and complex routines,
except where alternative words or phrases are indicated, for example
``symmetric/Hermitian'', ``orthogonal/unitary''
or ``quasi-triangular/triangular''. For the real routines
 is equivalent
to
is equivalent
to  .
(The same convention is used in Part
2.)
.
(The same convention is used in Part
2.)
- In a few cases, three routines are listed together, one for
real symmetric, one for complex symmetric, and one for complex Hermitian
matrices (for example SSPCON, CSPCON and CHPCON).
- A few routines for real matrices have no complex equivalent (for example
SSTEBZ).










Tue Nov 29 14:03:33 EST 1994
Availability of LAPACK





Next:
Installation of LAPACK
Up:
Essentials
Previous:
Documentation for LAPACK
The complete LAPACK package or individual routines from
LAPACK
are most easily obtained through
netlib
[32]
.
At the time of this writing, the e-mail addresses for netlib are
netlib@ornl.gov
netlib@research.att.com
Both repositories provide electronic mail and anonymous ftp service (the
netlib@ornl.gov cite is available via anonymous ftp to
netlib2.cs.utk.edu), and the
netlib@ornl.gov cite additionally provides xnetlib
. Xnetlib uses an X
Windows graphical user interface and a socket-based connection between
the user's machine and the xnetlib server machine to process software
requests. For more information on xnetlib, echo ``send index from
xnetlib'' | mail netlib@ornl.gov.
General information about LAPACK can be obtained by sending mail to one
of the above addresses with the message
send index from lapack
The package is also available on the World Wide Web. It can be accessed
through the URL address:
http://www.netlib.org/lapack/index.html
The complete package, including test code and timing programs in four
different Fortran data types, constitutes some 735,000 lines of Fortran
source and comments.
Alternatively, if a user does not have internet access, the complete
package can be obtained on magnetic media
from NAG for a cost-covering handling charge.
For further details contact NAG
at one of the following addresses:
NAG Inc. NAG Ltd.
1400 Opus Place, Suite 200 Wilkinson House
Downers Grove, IL 60515-5702 Jordan Hill Road
USA Oxford OX2 8DR
Tel: +1 708 971 2337 England
Fax: +1 708 971 2706 Tel: +44 865 511245
Fax: +44 865 310139
NAG GmbH
Schleissheimerstrasse 5
W-8046 Garching bei Munchen
Germany
Tel: +49 89 3207395
Fax: +49 89 3207396
Tue Nov 29 14:03:33 EST 1994
Index of Auxiliary Routines





Next:
Notes
Up:
Guide
Previous:
Notes
Tue Nov 29 14:03:33 EST 1994
Notes





Next:
Quick Reference
Guide
Up:
Index of Auxiliary
Previous:
Index of Auxiliary
- This index
lists related pairs of real and complex routines together,
in the same style as in Appendix A.
- Routines are listed in alphanumeric order
of the real (single precision) routine name (which always begins with S-).
(See subsection
2.1.3 for details of the LAPACK naming scheme.)
- A few complex routines have no real equivalents, and they are listed
first; routines listed in italics (for example, CROT), have real
equivalents in the Level 1 or Level 2 BLAS.
- Double precision routines are not listed here;
they have names beginning with D- instead of
S-, or Z- instead of C-.
The only exceptions to this simple rule are that
the double precision versions of ICMAX1, SCSUM1 and CSRSCL
are named IZMAX1, DZSUM1 and ZDRSCL.
- A few routines in the list have names that are independent of data type:
ILAENV, LSAME, LSAMEN and XERBLA.
- This index gives only a brief description of the purpose of each
routine. For a precise description consult the leading comments in the code,
which have been written in the same style as for the driver and
computational routines.







Tue Nov 29 14:03:33 EST 1994
Quick Reference<A NAME=7491>
</A>
Guide to the BLAS





Next:
Converting from LINPACK
Up:
Guide
Previous:
Notes
Level 1 BLAS
dim scalar vector vector scalars 5-element prefixes
array
SUBROUTINE _ROTG ( A, B, C, S ) S, D
SUBROUTINE _ROTMG( D1, D2, A, B, PARAM ) S, D
SUBROUTINE _ROT ( N, X, INCX, Y, INCY, C, S ) S, D
SUBROUTINE _ROTM ( N, X, INCX, Y, INCY, PARAM ) S, D
SUBROUTINE _SWAP ( N, X, INCX, Y, INCY ) S, D, C, Z
SUBROUTINE _SCAL ( N, ALPHA, X, INCX ) S, D, C, Z, CS, ZD
SUBROUTINE _COPY ( N, X, INCX, Y, INCY ) S, D, C, Z
SUBROUTINE _AXPY ( N, ALPHA, X, INCX, Y, INCY ) S, D, C, Z
FUNCTION _DOT ( N, X, INCX, Y, INCY ) S, D, DS
FUNCTION _DOTU ( N, X, INCX, Y, INCY ) C, Z
FUNCTION _DOTC ( N, X, INCX, Y, INCY ) C, Z
FUNCTION __DOT ( N, ALPHA, X, INCX, Y, INCY ) SDS
FUNCTION _NRM2 ( N, X, INCX ) S, D, SC, DZ
FUNCTION _ASUM ( N, X, INCX ) S, D, SC, DZ
FUNCTION I_AMAX( N, X, INCX ) S, D, C, Z

Level 2 BLAS
options dim b-width scalar matrix vector scalar vector prefixes
_GEMV ( TRANS, M, N, ALPHA, A, LDA, X, INCX, BETA, Y, INCY ) S, D, C, Z
_GBMV ( TRANS, M, N, KL, KU, ALPHA, A, LDA, X, INCX, BETA, Y, INCY ) S, D, C, Z
_HEMV ( UPLO, N, ALPHA, A, LDA, X, INCX, BETA, Y, INCY ) C, Z
_HBMV ( UPLO, N, K, ALPHA, A, LDA, X, INCX, BETA, Y, INCY ) C, Z
_HPMV ( UPLO, N, ALPHA, AP, X, INCX, BETA, Y, INCY ) C, Z
_SYMV ( UPLO, N, ALPHA, A, LDA, X, INCX, BETA, Y, INCY ) S, D
_SBMV ( UPLO, N, K, ALPHA, A, LDA, X, INCX, BETA, Y, INCY ) S, D
_SPMV ( UPLO, N, ALPHA, AP, X, INCX, BETA, Y, INCY ) S, D
_TRMV ( UPLO, TRANS, DIAG, N, A, LDA, X, INCX ) S, D, C, Z
_TBMV ( UPLO, TRANS, DIAG, N, K, A, LDA, X, INCX ) S, D, C, Z
_TPMV ( UPLO, TRANS, DIAG, N, AP, X, INCX ) S, D, C, Z
_TRSV ( UPLO, TRANS, DIAG, N, A, LDA, X, INCX ) S, D, C, Z
_TBSV ( UPLO, TRANS, DIAG, N, K, A, LDA, X, INCX ) S, D, C, Z
_TPSV ( UPLO, TRANS, DIAG, N, AP, X, INCX ) S, D, C, Z
options dim scalar vector vector matrix prefixes
_GER ( M, N, ALPHA, X, INCX, Y, INCY, A, LDA ) S, D
_GERU ( M, N, ALPHA, X, INCX, Y, INCY, A, LDA ) C, Z
_GERC ( M, N, ALPHA, X, INCX, Y, INCY, A, LDA ) C, Z
_HER ( UPLO, N, ALPHA, X, INCX, A, LDA ) C, Z
_HPR ( UPLO, N, ALPHA, X, INCX, AP ) C, Z
_HER2 ( UPLO, N, ALPHA, X, INCX, Y, INCY, A, LDA ) C, Z
_HPR2 ( UPLO, N, ALPHA, X, INCX, Y, INCY, AP ) C, Z
_SYR ( UPLO, N, ALPHA, X, INCX, A, LDA ) S, D
_SPR ( UPLO, N, ALPHA, X, INCX, AP ) S, D
_SYR2 ( UPLO, N, ALPHA, X, INCX, Y, INCY, A, LDA ) S, D
_SPR2 ( UPLO, N, ALPHA, X, INCX, Y, INCY, AP ) S, D
Level 3 BLAS
options dim scalar matrix matrix scalar matrix prefixes
_GEMM ( TRANSA, TRANSB, M, N, K, ALPHA, A, LDA, B, LDB, BETA, C, LDC ) S, D, C, Z
_SYMM ( SIDE, UPLO, M, N, ALPHA, A, LDA, B, LDB, BETA, C, LDC ) S, D, C, Z
_HEMM ( SIDE, UPLO, M, N, ALPHA, A, LDA, B, LDB, BETA, C, LDC ) C, Z
_SYRK ( UPLO, TRANS, N, K, ALPHA, A, LDA, BETA, C, LDC ) S, D, C, Z
_HERK ( UPLO, TRANS, N, K, ALPHA, A, LDA, BETA, C, LDC ) C, Z
_SYR2K( UPLO, TRANS, N, K, ALPHA, A, LDA, B, LDB, BETA, C, LDC ) S, D, C, Z
_HER2K( UPLO, TRANS, N, K, ALPHA, A, LDA, B, LDB, BETA, C, LDC ) C, Z
_TRMM ( SIDE, UPLO, TRANSA, DIAG, M, N, ALPHA, A, LDA, B, LDB ) S, D, C, Z
_TRSM ( SIDE, UPLO, TRANSA, DIAG, M, N, ALPHA, A, LDA, B, LDB ) S, D, C, Z


Notes
Meaning of prefixes
S - REAL C - COMPLEX
D - DOUBLE PRECISION Z - COMPLEX*16 (this may not be
supported by all
machines)
For the Level 2 BLAS a set of extended-precision routines with the prefixes
ES, ED, EC, EZ may also be available.
Level 1 BLAS
In addition to the listed routines there are two further
extended-precision dot product routines DQDOTI and DQDOTA.
Level 2 and Level 3 BLAS
Matrix types
GE - GEneral GB - General Band
SY - SYmmetric SB - Symmetric Band SP - Symmetric Packed
HE - HErmitian HB - Hermitian Band HP - Hermitian Packed
TR - TRiangular TB - Triangular Band TP - Triangular Packed
Options
Arguments describing options are declared as CHARACTER*1 and may be passed as character strings.
TRANS = 'No transpose', 'Transpose', 'Conjugate transpose' (X, X^T, X^C)
UPLO = 'Upper triangular', 'Lower triangular'
DIAG = 'Non-unit triangular', 'Unit triangular'
SIDE = 'Left', 'Right' (A or op(A) on the left, or A or op(A) on the right)
For real matrices, TRANS = `T' and TRANS = `C' have the same meaning.
For Hermitian matrices, TRANS = `T' is not allowed.
For complex symmetric matrices, TRANS = `H' is not allowed.
Tue Nov 29 14:03:33 EST 1994
Converting from LINPACK or EISPACK





Next:
Notes
Up:
Guide
Previous:
Quick Reference
Guide
This appendix
is designed to assist people to convert programs
that currently call LINPACK or EISPACK routines, to call LAPACK
routines instead.
Tue Nov 29 14:03:33 EST 1994
Notes





Next:
LAPACK Working Notes
Up:
Converting from LINPACK
Previous:
Converting from LINPACK
- The appendix consists mainly of indexes
giving the nearest LAPACK equivalents of LINPACK and EISPACK routines.
These indexes should not be followed blindly or rigidly,
especially when two or more
LINPACK or EISPACK routines are being used together: in many such cases
one of the LAPACK driver routines may be a suitable replacement.
- When two or more LAPACK routines are given in a single entry, these
routines must be combined to achieve the equivalent function.
- For LINPACK, an index is given for equivalents of the real LINPACK
routines; these equivalences apply also to the corresponding complex routines.
A separate table is included for equivalences of complex Hermitian routines.
For EISPACK, an index is given for all real and complex routines,
since there is no direct 1-to-1 correspondence between real and complex
routines in EISPACK.
- A few of the less commonly used routines in LINPACK and EISPACK have no
equivalents in Release 1.0 of LAPACK; equivalents for some of these (but not
all) are planned for a future release.
- For some EISPACK routines, there are LAPACK routines providing similar
functionality, but using a significantly different method, or LAPACK routines
which provide only part of the functionality; such routines are marked by
a
 . For example, the EISPACK routine ELMHES uses non-orthogonal
transformations, whereas the nearest equivalent LAPACK routine, SGEHRD, uses
orthogonal transformations.
. For example, the EISPACK routine ELMHES uses non-orthogonal
transformations, whereas the nearest equivalent LAPACK routine, SGEHRD, uses
orthogonal transformations.
- In some cases the LAPACK equivalents require matrices to be stored
in a different storage scheme. For example:
- EISPACK routines BANDR
, BANDV
,
BQR
and the driver routine RSB
require the lower triangle of
a symmetric band matrix to be stored in
a different storage scheme to that used in LAPACK, which is illustrated in
subsection
5.3.3. The corresponding storage scheme used by the
EISPACK routines is:

- EISPACK routines TRED1
, TRED2
,
TRED3
, HTRID3
,
HTRIDI
, TQL1
,
TQL2
, IMTQL1
,
IMTQL2
, RATQR
,
TQLRAT
and the driver routine RST
store the off-diagonal elements of a symmetric tridiagonal
matrix in elements 2 : n of the array E, whereas LAPACK routines use
elements 1 : n - 1.
- The EISPACK and LINPACK routines for the singular value decomposition
return the matrix of right singular vectors, V, whereas the corresponding
LAPACK routines return the transposed matrix
 .
.
- In general, the argument lists of the
LAPACK routines are different from those of
the corresponding EISPACK and LINPACK
routines, and the workspace requirements are often different.

LAPACK equivalents of LINPACK routines for real matrices
----------------------------------------------------------------
LINPACK LAPACK Function of LINPACK routine
----------------------------------------------------------------
SCHDC Cholesky factorization with diagonal pivoting
option
----------------------------------------------------------------
SCHDD rank-1 downdate of a Cholesky factorization
or the triangular factor of a QR factorization
----------------------------------------------------------------
SCHEX rank-1 update of a Cholesky factorization
or the triangular factor of a QR factorization
----------------------------------------------------------------
SCHUD modifies a Cholesky factorization under
permutations of the original matrix
----------------------------------------------------------------
SGBCO SLANGB LU factorization and condition estimation
SGBTRF of a general band matrix
SGBCON
----------------------------------------------------------------
SGBDI determinant of a general band matrix,
after factorization by SGBCO or SGBFA
----------------------------------------------------------------
SGBFA SGBTRF LU factorization of a general band matrix
----------------------------------------------------------------
SGBSL SGBTRS solves a general band system of linear
equations, after factorization by SGBCO
or SGBFA
----------------------------------------------------------------
SGECO SLANGE LU factorization and condition
SGETRF estimation of a general matrix
SGECON
----------------------------------------------------------------
SGEDI SGETRI determinant and inverse of a general
matrix, after factorization by SGECO
or SGEFA
----------------------------------------------------------------
SGEFA SGETRF LU factorization of a general matrix
----------------------------------------------------------------
SGESL SGETRS solves a general system of linear
equations, after factorization by
SGECO or SGEFA
----------------------------------------------------------------
SGTSL SGTSV solves a general tridiagonal system
of linear equations
----------------------------------------------------------------
SPBCO SLANSB Cholesky factorization and condition
SPBTRF estimation of a symmetric positive definite
SPBCON band matrix
----------------------------------------------------------------
SPBDI determinant of a symmetric positive
definite band matrix, after factorization
by SPBCO or SPBFA
----------------------------------------------------------------
SPBFA SPBTRF Cholesky factorization of a symmetric
positive definite band matrix
----------------------------------------------------------------
SPBSL SPBTRS solves a symmetric positive definite band
system of linear equations, after
factorization by SPBCO or SPBFA
----------------------------------------------------------------
SPOCO SLANSY Cholesky factorization and condition
SPOTRF estimation of a symmetric positive definite
SPOCON matrix
----------------------------------------------------------------
SPODI SPOTRI determinant and inverse of a symmetric
positive definite matrix, after factorization
by SPOCO or SPOFA
----------------------------------------------------------------
SPOFA SPOTRF Cholesky factorization of a symmetric
positive definite matrix
----------------------------------------------------------------
SPOSL SPOTRS solves a symmetric positive definite system
of linear equations, after factorization by
SPOCO or SPOFA
----------------------------------------------------------------
SPPCO SLANSY Cholesky factorization and condition
SPPTRF estimation of a symmetric positive definite
SPPCON matrix (packed storage)
----------------------------------------------------------------
LAPACK equivalents of LINPACK
routines for real matrices(continued)
----------------------------------------------------------------
LINPACK LAPACK Function of LINPACK routine}\\
----------------------------------------------------------------
SPPDI SPPTRI determinant and inverse of a symmetric
positive definite matrix, after factorization
by SPPCO or SPPFA (packed storage)
----------------------------------------------------------------
SPPFA SPPTRF Cholesky factorization of a symmetric
positive definite matrix (packed storage)
----------------------------------------------------------------
SPPSL SPPTRS solves a symmetric positive definite system
of linear equations, after factorization by
SPPCO or SPPFA (packed storage)
----------------------------------------------------------------
SPTSL SPTSV solves a symmetric positive definite
tridiagonal system of linear equations
----------------------------------------------------------------
SQRDC SGEQPF QR factorization with optional column
or pivoting
SGEQRF
----------------------------------------------------------------
SQRSL SORMQR solves linear least squares problems after
STRSV factorization by SQRDC
----------------------------------------------------------------
SSICO SLANSY symmetric indefinite factorization and
SSYTRF condition estimation of a symmetric
SSYCON indefinite matrix
----------------------------------------------------------------
SSIDI SSYTRI determinant, inertia and inverse of a
symmetric indefinite matrix, after
factorization by SSICO or SSIFA
----------------------------------------------------------------
SSIFA SSYTRF symmetric indefinite factorization of a
symmetric indefinite matrix
----------------------------------------------------------------
SSISL SSYTRS solves a symmetric indefinite system of
linear equations, after factorization by
SSICO or SSIFA
----------------------------------------------------------------
SSPCO SLANSP symmetric indefinite factorization and
SSPTRF condition estimation of a symmetric
SSPCON indefinite matrix (packed storage)
----------------------------------------------------------------
SSPDI SSPTRI determinant, inertia and inverse of a
symmetric indefinite matrix, after
factorization by SSPCO or SSPFA (packed
storage)
----------------------------------------------------------------
SSPFA SSPTRF symmetric indefinite factorization of a
symmetric indefinite matrix (packed storage)
----------------------------------------------------------------
SSPSL SSPTRS solves a symmetric indefinite system of
linear equations, after factorization by
SSPCO or SSPFA (packed storage)
----------------------------------------------------------------
SSVDC SGESVD all or part of the singular value
decomposition of a general matrix
----------------------------------------------------------------
STRCO STRCON condition estimation of a triangular matrix
----------------------------------------------------------------
STRDI STRTRI determinant and inverse of a triangular
matrix
----------------------------------------------------------------
STRSL STRTRS solves a triangular system of linear
equations
----------------------------------------------------------------








Next:
LAPACK Working Notes
Up:
Converting from LINPACK
Previous:
Converting from LINPACK
Tue Nov 29 14:03:33 EST 1994
LAPACK Working Notes





Next:
Specifications of Routines
Up:
Guide
Previous:
Notes
Most of these working notes are available from netlib, where they
can only be obtained in postscript form.
To receive a list of available postscript reports, send email to
netlib@ornl.gov of the form: send index from lapack/lawns
- 1.
- J. W. DEMMEL, J. J. DONGARRA, J. DU CROZ, A. GREENBAUM,
S. HAMMARLING, AND D. SORENSEN,
Prospectus for the Development of a Linear Algebra Library
for High-Performance Computers,
ANL, MCS-TM-97, September 1987.
- 2.
- J. J. DONGARRA, S. HAMMARLING, AND D. SORENSEN,
Block Reduction of Matrices to Condensed Forms for Eigenvalue
Computations,
ANL, MCS-TM-99, September 1987.
- 3.
- J. W. DEMMEL AND W. KAHAN,
Computing Small Singular Values of Bidiagonal Matrices with
Guaranteed High Relative Accuracy,
ANL, MCS-TM-110, February 1988.
- 4.
- J. W. DEMMEL, J. DU CROZ, S. HAMMARLING, AND D. SORENSEN,
Guidelines for the Design of Symmetric Eigenroutines, SVD, and
Iterative Refinement and Condition Estimation for Linear Systems,
ANL, MCS-TM-111, March 1988.
- 5.
- C. BISCHOF, J. W. DEMMEL, J. J. DONGARRA, J. DU CROZ,
A. GREENBAUM, S. HAMMARLING, AND D. SORENSEN,
Provisional Contents,
ANL, MCS-TM-38, September 1988.
- 6.
- O. BREWER, J. J. DONGARRA, AND D. SORENSEN,
Tools to Aid in the Analysis of Memory Access Patterns for FORTRAN
Programs,
ANL, MCS-TM-120, June 1988.
- 7.
- J. BARLOW AND J. W. DEMMEL,
Computing Accurate Eigensystems of Scaled Diagonally Dominant Matrices,
ANL, MCS-TM-126, December 1988.
- 8.
- Z. BAI AND J. W. DEMMEL,
On a Block Implementation of Hessenberg Multishift QR Iteration,
ANL, MCS-TM-127, January 1989.
- 9.
- J. W. DEMMEL AND A. MCKENNEY,
A Test Matrix Generation Suite,
ANL, MCS-P69-0389, March 1989.
- 10.
- E. ANDERSON AND J. J. DONGARRA,
Installing and Testing the Initial Release of LAPACK -
Unix and Non-Unix Versions,
ANL, MCS-TM-130, May 1989.
- 11.
- P. DEIFT, J. W. DEMMEL, L.-C. LI, AND C. TOMEI,
The Bidiagonal Singular Value Decomposition and Hamiltonian
Mechanics,
ANL, MCS-TM-133, August 1989.
- 12.
- P. MAYES AND G. RADICATI,
Banded Cholesky Factorization Using Level 3 BLAS,
ANL, MCS-TM-134, August 1989.
- 13.
- Z. BAI, J. W. DEMMEL, AND A. MCKENNEY,
On the Conditioning of the Nonsymmetric Eigenproblem:
Theory and Software,
UT, CS-89-86, October 1989.
- 14.
- J. W. DEMMEL,
On Floating-Point Errors in Cholesky,
UT, CS-89-87, October 1989.
- 15.
- J. W. DEMMEL AND K. VESELIC,
Jacobi's Method is More Accurate than QR,
UT, CS-89-88, October 1989.
- 16.
- E. ANDERSON AND J. J. DONGARRA,
Results from the Initial Release of LAPACK,
UT, CS-89-89, November 1989.
- 17.
- A. GREENBAUM AND J. J. DONGARRA,
Experiments with QR/QL Methods for the Symmetric Tridiagonal
Eigenproblem,
UT, CS-89-92, November 1989.
- 18.
- E. ANDERSON AND J. J. DONGARRA,
Implementation Guide for LAPACK,
UT, CS-90-101, April 1990.
- 19.
- E. ANDERSON AND J. J. DONGARRA,
Evaluating Block Algorithm Variants in LAPACK,
UT, CS-90-103, April 1990.
- 20.
- E. ANDERSON, Z. BAI, C. BISCHOF, J. W. DEMMEL,
J. J. DONGARRA, J. DU CROZ, A. GREENBAUM, S. HAMMARLING, A. MCKENNEY,
AND D. SORENSEN,
LAPACK: A Portable Linear Algebra Library for High-Performance
Computers,
UT, CS-90-105, May 1990.
- 21.
- J. DU CROZ, P. MAYES, AND G. RADICATI,
Factorizations of Band Matrices Using Level 3 BLAS,
UT, CS-90-109, July 1990.
- 22.
- J. W. DEMMEL AND N. J. HIGHAM,
Stability of Block Algorithms with Fast Level 3 BLAS,
UT, CS-90-110, July 1990.
- 23.
- J. W. DEMMEL AND N. J. HIGHAM,
Improved Error Bounds for Underdetermined System Solvers,
UT, CS-90-113, August 1990.
- 24.
- J. J. DONGARRA AND S. OSTROUCHOV,
LAPACK Block Factorization Algorithms on the Intel iPSC/860,
UT, CS-90-115, October, 1990.
- 25.
- J. J. DONGARRA, S. HAMMARLING, AND J. H. WILKINSON,
Numerical Considerations in Computing Invariant Subspaces,
UT, CS-90-117, October, 1990.
- 26.
- E. ANDERSON, C. BISCHOF, J. W. DEMMEL, J. J. DONGARRA,
J. DU CROZ, S. HAMMARLING, AND W. KAHAN,
Prospectus for an Extension to LAPACK: A Portable Linear Algebra
Library for High-Performance Computers,
UT, CS-90-118, November 1990.
- 27.
- J. DU CROZ AND N. J. HIGHAM,
Stability of Methods for Matrix Inversion,
UT, CS-90-119, October, 1990.
- 28.
- J. J. DONGARRA, P. MAYES, AND G. RADICATI,
The IBM RISC System/6000 and Linear Algebra Operations,
UT, CS-90-122, December 1990.
- 29.
- R. VAN DE GEIJN,
On Global Combine Operations,
UT, CS-91-129, April 1991.
- 30.
- J. J. DONGARRA AND R. VAN DE GEIJN,
Reduction to Condensed Form for the Eigenvalue Problem on
Distributed Memory Architectures,
UT, CS-91-130, April 1991.
- 31.
- E. ANDERSON, Z. BAI, AND J. J. DONGARRA,
Generalized QR Factorization and its Applications,
UT, CS-91-131, April 1991.
- 32.
- C. BISCHOF AND P. TANG,
Generalized Incremental Condition Estimation,
UT, CS-91-132, May 1991.
- 33.
- C. BISCHOF AND P. TANG,
Robust Incremental Condition Estimation,
UT, CS-91-133, May 1991.
- 34.
- J. J. DONGARRA,
Workshop on the BLACS,
UT, CS-91-134, May 1991.
- 35.
- E. ANDERSON, J. J. DONGARRA, AND S. OSTROUCHOV,
Implementation guide for LAPACK,
UT, CS-91-138, August 1991. (replaced by Working Note 41)
- 36.
- E. ANDERSON, Robust Triangular Solves for
Use in Condition Estimation, UT, CS-91-142, August 1991.
- 37.
- J. J. DONGARRA AND R. VAN DE GEIJN,
Two Dimensional Basic Linear Algebra Communication
Subprograms, UT, CS-91-138, October 1991.
- 38.
-
Z. BAI AND J. W. DEMMEL,
On a Direct Algorithm for Computing Invariant Subspaces with
Specified Eigenvalues, UT, CS-91-139, November 1991.
- 39.
- J. W. DEMMEL, J. J. DONGARRA, AND W. KAHAN,
On Designing Portable High Performance Numerical Libraries,
UT, CS-91-141, July 1991.
- 40.
- J. W. DEMMEL, N. J. HIGHAM, AND R. SCHREIBER,
Block LU Factorization,
UT, CS-92-149, February 1992.
- 41.
- E. ANDERSON, J. J. DONGARRA, AND S. OSTROUCHOV,
Installation Guide for LAPACK,
UT, CS-92-151, February 1992.
- 42.
- N. J. HIGHAM, Perturbation Theory and Backward Error
for AX-XB=C., UT, CS-92-153, April, 1992.
- 43.
- J. J. DONGARRA, R. VAN DE GEIJN, AND D. W. WALKER,
A Look at Scalable Dense Linear Algebra Libraries,
UT, CS-92-155, April, 1992.
- 44.
- E. ANDERSON AND J. J. DONGARRA,
Performance of LAPACK: A Portable Library of Numerical Linear
Algebra Routines, UT, CS-92-156, May 1992.
- 45.
- J. W. DEMMEL,
The Inherent Inaccuracy of Implicit Tridiagonal QR,
UT, CS-92-162, May 1992.
- 46.
- Z. BAI AND J. W. DEMMEL,
Computing the Generalized Singular Value Decomposition,
UT, CS-92-163, May 1992.
- 47.
- J. W. DEMMEL,
Open Problems in Numerical Linear Algebra,
UT, CS-92-164, May 1992.
- 48.
- J. W. DEMMEL AND W. GRAGG,
On Computing Accurate Singular Values and Eigenvalues of Matrices
with Acyclic Graphs,
UT, CS-92-166, May 1992.
- 49.
- J. W. DEMMEL,
A Specification for Floating Point Parallel Prefix,
UT, CS-92-167, May 1992.
- 50.
- V. EIJKHOUT,
Distributed Sparse Data Structures for Linear Algebra Operations,
UT, CS-92-169, May 1992.
- 51.
- V. EIJKHOUT,
Qualitative Properties of the Conjugate Gradient and Lanczos Methods
in a Matrix Framework,
UT, CS-92-170, May 1992.
- 52.
- M. T. HEATH AND P. RAGHAVAN,
A Cartesian Parallel Nested Dissection Algorithm,
UT, CS-92-178, June 1992.
- 53.
- J. W. DEMMEL,
Trading Off Parallelism and Numerical Stability,
UT, CS-92-179, June 1992.
- 54.
- Z. BAI AND J. W. DEMMEL,
On Swapping Diagonal Blocks in Real Schur Form,
UT, CS-92-182, October 1992.
- 55.
- J. CHOI, J. J. DONGARRA, R. POZO, AND D. W. WALKER,
ScaLAPACK: A Scalable Linear Algebra for Distributed Memory
Concurrent Computers,
UT, CS-92-181, November 1992.
- 56.
- E. F. D'AZEVEDO, V. L. EIJKHOUT AND C. H. ROMINE,
Reducing Communication Costs in the Conjugate Gradient Algorithm
on Distributed Memory Multiprocessors,
UT, CS-93-185, January 1993.
- 57.
- J. CHOI, J. J. DONGARRA, AND D. W. WALKER,
PUMMA: Parallel Universal Matrix Multiplication Algorithms on
Distributed Memory Concurrent Computers,
UT, CS-93-187, May 1993.
- 58.
- J. J. DONGARRA AND D. W. WALKER,
The Design of Linear Algebra Libraries for High Performance Computer,
UT, CS-93-188, June 1993.
- 59.
- J. W. DEMMEL AND X. LI,
Faster Numerical Algorithms via Exception Handling,
UT, CS-93-192, March 1993.
- 60.
- J. W. DEMMEL, M. T. HEATH, AND H. A. VAN DER VORST,
Parallel Numerical Linear Algebra,
UT, CS-93-192, March 1993.
- 61.
- J. J. DONGARRA, R. POZO, AND D. W. WALKER,
An Object Oriented Design for High Performance Linear Algebra on
Distributed Memory Architectures,
UT, CS-93-200, August 1993.
- 62.
- M. T. HEATH AND P. RAGHAVAN,
Distributed Solution of Sparse Linear Systems,
UT, CS-93-201, August 1993.
- 63.
- M. T. HEATH AND P. RAGHAVAN,
Line and Plane Separators,
UT, CS-93-202, August 1993.
- 64.
- P. RAGHAVAN,
Distributed Sparse Gaussian Elimination and Orthogonal Factorization,
UT, CS-93-203, August 1993.
- 65.
- J. CHOI, J. J. DONGARRA, AND D. W. WALKER,
Parallel Matrix Transpose Algorithms on Distributed Memory
Concurrent Computers,
UT, CS-93-215, November, 1993.
- 66.
- V. L. EIJKHOUT,
A Characterization of Polynomial Iterative Methods,
UT, CS-93-216, November, 1993.
- 67.
- F. DESPREZ, J. DONGARRA, AND B. TOURANCHEAU,
Performance Complexity of
 Factorization with Efficient
Pipelining and Overlap on a Multiprocessor,
UT, CS-93-218, December, 1993.
Factorization with Efficient
Pipelining and Overlap on a Multiprocessor,
UT, CS-93-218, December, 1993.
- 68.
- MICHAEL W. BERRY, JACK J. DONGARRA AND YOUNGBAE KIM,
A Highly Parallel Algorithm for the Reduction of a Nonsymmetric
Matrix to Block Upper-Hessenberg Form,
UT, CS-94-221, January, 1994.
- 69.
- J. RUTTER,
A Serial Implementation of Cuppen's Divide and Conquer
Algorithm for the Symmetric Eigenvalue Problem,
UT, CS-94-225, March, 1994.
- 70.
- J. W. DEMMEL, INDERJIT DHILLON, AND HUAN REN,
On the Correctness of Parallel Bisection in Floating Point,
UT, CS-94-228, April, 1994.
- 71.
- J. DONGARRA AND M. KOLATIS,
IBM RS/6000-550 & -590 Performance for Selected Routines in ESSL,
UT, CS-94-231, April, 1994.
- 72.
- R. LEHOUCQ,
The Computation of Elementary Unitary Matrices,
UT, CS-94-233, May, 1994.
- 73.
- R. CLINT WHALEY,
Basic Linear Algebra Communication Subprograms: Analysis and
Implementation Across Multiple Parallel Architectures,
UT, CS-94-234, May, 1994.
- 74.
- J. DONGARRA, A. LUMSDAINE, X. NIU, R. POZO, AND K.
REMINGTON,
A Sparse Matrix Library in C++ for High Performance Architectures,
UT, CS-94-236, July, 1994.
- 75.
- B. KÅGSTRÖM AND P. POROMAA,
Computing Eigenspaces with Specified Eigenvalues of a Regular
Matrix Pair (A,B) and Condition Estimation: Theory, Algorithms and
Software,
UT, CS-94-237, July, 1994.
- 76.
- R. BARRETT, M. BERRY, J. DONGARRA, V. EIJKHOUT, AND C.
ROMINE, Algorithic Bombardment for the Iterative Solution of
Linear Systems: A Poly-Iterative Approach,
UT, CS-94-239, August, 1994.
- 77.
- V. EIJKHOUT AND R. POZO,
Basic Concepts for Distributed Sparse Linear Algebra Operations,
UT, CS-94-240, August, 1994.
- 78.
- V. EIJKHOUT,
Computational variants of the CGS and BiCGstab methods,
UT, CS-94-241, August, 1994.
- 79.
- G. HENRY AND R. VAN DE GEIJN,
Parallelizing the QR Algorithm for the Unsymmetric Algebraic
Eigenvalue Problem: Myths and Reality,
UT, CS-94-244, August, 1994.
- 80.
- J. CHOI, J. J. DONGARRA, S. OSTROUCHOV, A. P. PETITET,
D. W. WALKER, AND R. C. WHALEY,
The Design and Implementation of the ScaLAPACK LU, QR, and
Cholesky Factorization Routines,
UT, CS-94-246, September, 1994.
- 81.
- J. J. DONGARRA AND S. OSTROUCHOV,
Quick Installation Guide for LAPACK on Unix Systems,
UT, CS-94-249, September, 1994.
- 82.
- J. J. DONGARRA AND M. KOLATIS,
Call Conversion Interface (CCI) for LAPACK/ESSL,
UT, CS-94-250, August, 1994.
- 83.
- R. C. LI, Relative Perturbation Bounds for the
Unitary Polar Factor, UT, CS-94-251, September, 1994.
- 84.
- R. C. LI, Relative Perturbation Theory: (I)
Eigenvalue Variations, UT, CS-94-252, September, 1994.
- 85.
- R. C. LI, Relative Perturbation Theory: (II)
Eigenspace Variations, UT, CS-94-253, September, 1994.
- 86.
- J. DEMMEL AND K. STANLEY,
The Performance of Finding Eigenvalues and Eigenvectors of
Dense Symmetric Matrices on Distributed Memory Computers,
UT, CS-94-254, September, 1994.
- 87.
- B. KÅGSTRÖM AND P. POROMAA,
Computing Eigenspaces with Specified Eigenvalues of a
Regular Matrix Pair (A,B) and Condition Estimation: Theory,
Algorithms and Software,
UT, CS-94-255, September, 1994.





Next:
Specifications of Routines
Up:
Guide
Previous:
Notes
Tue Nov 29 14:03:33 EST 1994
Specifications of Routines





Next:
Notes
Up:
LAPACK Users' Guide Release
Previous:
LAPACK Working Notes
Tue Nov 29 14:03:33 EST 1994
Notes





Next:
References
Up:
Specifications of Routines
Previous:
Specifications of Routines
- The specifications that follow give the calling sequence, purpose,
and descriptions of the arguments of each LAPACK driver and
computational routine (but not of auxiliary routines).
- Specifications of pairs of real and complex routines have been merged
(for example SBDSQR/CBDSQR).
In a few cases, specifications of three routines have been merged, one for
real symmetric, one for complex symmetric, and one for complex Hermitian
matrices (for example SSYTRF/CSYTRF/CHETRF).
A few routines for real matrices have no complex equivalent (for example
SSTEBZ).
- Specifications are given only for single precision routines.
To adapt them for the double precision version of the software, simply
interpret REAL as DOUBLE PRECISION, COMPLEX as COMPLEX*16 (or DOUBLE COMPLEX),
and the initial letters S- and C- of LAPACK routine names as D- and Z-.
- Specifications are arranged in alphabetical order of the real routine
name.
- The text of the specifications has been derived from the leading comments
in the source-text of the routines. It makes only a limited use of
mathematical typesetting facilities. To eliminate redundancy,
 has been used throughout the specifications. Thus, the reader should
note that
has been used throughout the specifications. Thus, the reader should
note that  is equivalent to
is equivalent to  in the real case.
in the real case.
- If there is a discrepancy between the specifications listed in
this section and the actual source code, the source code should be
regarded as the most up-to-date.
=0.15in
=-.4in
Tue Nov 29 14:03:33 EST 1994
References





Next:
Index
Up:
LAPACK Users' Guide Release
Previous:
Notes
References
-
1
-
E. ANDERSON, Z. BAI, C. BISCHOF, J. W. DEMMEL, J. J. DONGARRA, J. DU CROZ,
A. GREENBAUM, S. HAMMARLING, A. MCKENNEY, AND D. SORENSEN, LAPACK: A
portable linear algebra library for high-performance computers, Computer
Science Dept. Technical Report CS-90-105, University of Tennessee,
Knoxville, 1990.
(LAPACK Working Note 20).
-
2
-
E. ANDERSON, Z. BAI, AND J. J. DONGARRA,
Generalized QR Factorization and its Applications,
Computer Science Dept. Technical Report CS-91-131,
University of Tennessee, Knoxville, 1991.
(LAPACK Working Note 31).
-
3
-
E. ANDERSON, J. J. DONGARRA, AND S. OSTROUCHOV, Installation guide
for LAPACK, Computer Science Dept. Technical Report CS-92-151,
University of Tennessee, Knoxville, 1992.
(LAPACK Working Note 41).
-
4
-
ANSI/IEEE, IEEE Standard for Binary Floating-Point Arithmetic, New York, Std
754-1985 ed., 1985.
-
5
-
ANSI/IEEE, IEEE Standard for Radix Independent Floating Point Arithmetic,
New York, Std 854-1987 ed., 1987.
-
6
-
M. ARIOLI, J. W. DEMMEL, AND I. S. DUFF, Solving sparse linear
systems with sparse backward error, SIAM J. Matrix Anal. Appl., 10 (1989),
pp. 165-190.
-
7
-
M. ARIOLI, I. S. DUFF, AND P. P. M. DE RIJK, On the augmented system
approach to sparse least squares problems, Num. Math., 55 (1989),
pp. 667-684.
-
8
-
Z. BAI AND J. W. DEMMEL, On a block implementation of Hessenberg
multishift QR iteration, Int. J. of High Speed Comput., 1
(1989), pp. 97-112.
(LAPACK Working Note 8).
-
9
-
Z. BAI AND J. W. DEMMEL,
Design of a parallel nonsymmetric eigenroutine toolbox, Part I,
Proceedings of the Sixth SIAM Conference on Parallel Proceesing for Scientific
Computing, SIAM (1993), pp. 391-398.
-
10
-
Z. BAI AND J. W. DEMMEL,
Computing the generalized singular value decomposition,
SIAM J. Sci. Comp., 14 (1993), pp. 1464-1486.
(LAPACK Working Note 46).
-
11
-
Z. BAI, J. W. DEMMEL, AND A. MCKENNEY, On computing condition
numbers for the nonsymmetric eigenproblem, ACM Trans. Math. Soft. 19
(1993), pp. 202-223.
(LAPACK Working Note 13).
-
12
-
Z. BAI AND H. ZHA,
A new preprocessing algorithm for the computation of the
generalized singular value decomposition,
SIAM J. Sci. Comp., 14 (1993), pp. 1007-1012.
-
13
-
J. BARLOW AND J. DEMMEL, Computing accurate eigensystems of scaled
diagonally dominant matrices, SIAM J. Num. Anal., 27 (1990), pp. 762-791.
(LAPACK Working Note 7).
-
14
-
C. R. CRAWFORD,
Reduction of a band-symmetric generalized eigenvalue problem,
Comm. ACM, 16 (1973), pp. 41-44.
-
15
-
J. J. M. CUPPEN,
A divide and conquer method for the symmetric tridiagonal eigenproblem,
Numerische Math., 36 (1981), pp. 177-195.
-
16
-
P. DEIFT, J. W. DEMMEL, L.-C. LI, AND C. TOMEI, The bidiagonal
singular value decomposition and Hamiltonian mechanics, SIAM J. Num.
Anal., 28 (1991), pp. 1463-1516.
(LAPACK Working Note 11).
-
17
-
J. W. DEMMEL, The Condition Number of Equivalence Transformations
that Block Diagonalize Matrix Pencils,
SIAM J. Num. Anal., 20 (1983), pp. 599-610.
-
18
-
J. W. DEMMEL, Underflow and the
Reliability of Numerical Software, SIAM J. Sci. Stat. Comput., 5 (1984),
pp. 887-919.
-
19
-
J. W. DEMMEL AND N. J. HIGHAM, Improved error bounds for
underdetermined systems solvers, SIAM J. Matrix Anal. Appl., 14 (1993),
pp. 1-14.
-
20
-
J. W. DEMMEL AND N. J. HIGHAM, Stability of block
algorithms with fast level 3 BLAS, ACM Trans. Math. Soft., 18 (1992),
pp. 274-291.
(LAPACK Working Note 22).
-
21
-
J. W. DEMMEL AND B. KåGSTRÖM, Computing Stable
Eigendecompositions of Matrix Pencils, Lin. Alg. Appl., 88/89 (1987),
pp. 139-186.
-
22
-
J. W. DEMMEL AND W. KAHAN, Accurate singular values of bidiagonal
matrices, SIAM J. Sci. Stat. Comput., 11 (1990), pp. 873-912.
(LAPACK Working Note 3).
-
23
-
J. W. DEMMEL AND X. LI,
Faster Numerical Algorithms via Exception Handling,
IEEE Trans. Comp., 43 (1994), pp. 983-992.
(LAPACK Working Note 59).
-
24
-
J. W. DEMMEL AND K. VESELIC, Jacobi's method is more accurate
than QR, SIAM J. Matrix Anal. Appl. 13 (1992), pp. 1204-1246.
(LAPACK Working Note 15).
-
25
-
B. DE MOOR AND P. VAN DOOREN,
Generalization of the singular value and QR decompositions,
SIAM J. Matrix Anal. Appl., 13 (1992), pp. 993-1014.
-
26
-
J. J. DONGARRA, J. R. BUNCH, C. B. MOLER, AND G. W. STEWART, LINPACK
Users' Guide, SIAM, Philadelphia, PA, 1979.
-
27
-
J. J. DONGARRA, J. DU CROZ, I. S. DUFF, AND S. HAMMARLING, Algorithm
679: A set of Level 3 Basic Linear Algebra Subprograms, ACM
Trans. Math. Soft., 16 (1990), pp. 18-28.
-
28
-
J. J. DONGARRA, J. DU CROZ, I. S. DUFF, AND S. HAMMARLING, A set of Level 3
Basic Linear Algebra Subprograms, ACM Trans. Math. Soft., 16
(1990), pp. 1-17.
-
29
-
J. J. DONGARRA, J. DU CROZ, S. HAMMARLING, AND R. J. HANSON, Algorithm 656: An extended set of FORTRAN Basic Linear Algebra
Subprograms, ACM Trans. Math. Soft., 14 (1988), pp. 18-32.
-
30
-
J. J. DONGARRA, J. DU CROZ, S. HAMMARLING, AND R. J. HANSON, An extended set of
FORTRAN Basic Linear Algebra Subprograms, ACM Trans. Math. Soft., 14
(1988), pp. 1-17.
-
31
-
J. J. DONGARRA, I. S. DUFF, D. C. SORENSEN, AND H. A. VAN DER VORST, Solving Linear Systems on Vector and Shared Memory Computers, SIAM
Publications, 1991.
-
32
-
J. J. DONGARRA AND E. GROSSE, Distribution of mathematical software
via electronic mail, Communications of the ACM, 30 (1987), pp. 403-407.
-
33
-
J. J. DONGARRA, F. G. GUSTAFSON, AND A. KARP, Implementing linear
algebra algorithms for dense matrices on a vector pipeline machine, SIAM
Review, 26 (1984), pp. 91-112.
-
34
-
J. J. DONGARRA, S. HAMMARLING, AND D. C. SORENSEN, Block reduction
of matrices to condensed forms for eigenvalue computations, JCAM, 27
(1989), pp. 215-227.
(LAPACK Working Note 2).
-
35
-
J. J. DONGARRA AND S. OSTROUCHOV, Quick installation guide
for LAPACK on unix systems, Computer Science Dept. Technical
Report CS-94-249, University of Tennessee, Knoxville, 1994.
(LAPACK Working Note 81).
-
36
-
J. J. DONGARRA, R. POZO, AND D. WALKER,
An object oriented design for high performance linear algebra on
distributed memory architectures, Computer Science Dept. Technical
Report CS-93-200, University of Tennessee, Knoxville, 1993.
(LAPACK Working Note 61).
-
37
-
A. DUBRULLE, The multishift QR algorithm: is it worth the
trouble?, Palo Alto Scientific Center Report G320-3558x, IBM Corp.,
Palo Alto, 1991.
-
38
-
J. DU CROZ AND N. J. HIGHAM, Stability of methods for matrix
inversion, IMA J. Num. Anal., 12 (1992), pp. 1-19.
(LAPACK Working Note 27).
-
39
-
J. DU CROZ, P. J. D. MAYES, AND G. RADICATI DI BROZOLO, Factorizations of band matrices using Level 3 BLAS, Computer Science
Dept. Technical Report CS-90-109, University of Tennessee, Knoxville,
1990.
(LAPACK Working Note 21).
-
40
-
S. I. FELDMAN, D. M. GAY, M. W. MAIMONE, AND N. L. SCHRYER,
A Fortran-to-C Converter, Computing Science Technical
Report No. 149, AT & T Bell Laboratories, Murray Hill, NJ, 1990.
-
41
-
V. FERNANDO AND B. PARLETT,
Accurate singular values and differential qd algorithms,
Numerisch Math. 67 (1994), pp. 191-229.
-
42
-
K. A. GALLIVAN, R. J. PLEMMONS, AND A. H. SAMEH, Parallel algorithms
for dense linear algebra computations, SIAM Review, 32 (1990),
pp. 54-135.
-
43
-
F. GANTMACHER,
The Theory of Matrices, vol. II (transl.),
Chelsea Publishers, New York, 1959.
-
44
-
B. S. GARBOW, J. M. BOYLE, J. J. DONGARRA, AND C. B. MOLER, Matrix
Eigensystem Routines - EISPACK Guide Extension, vol. 51 of Lecture Notes
in Computer Science, Springer-Verlag, Berlin, 1977.
-
45
-
G. GOLUB AND C. F. VAN LOAN, Matrix Computations, Johns Hopkins
University Press, Baltimore, MD, 2nd ed., 1989.
-
46
-
A. GREENBAUM AND J. J. DONGARRA, Experiments with QL/QR methods
for the symmetric tridiagonal eigenproblem, Computer Science Dept.
Technical Report CS-89-92, University of Tennessee, Knoxville, 1989.
(LAPACK Working Note 17).
-
47
-
M. GU AND S. EISENSTAT,
A stable algorithm for the rank-1 modification of the symmetric
eigenproblem, Yale University, Computer Science Department Report
YALEU/DCS/RR-916, New Haven, CT (1992).
-
48
-
W. W. HAGER, Condition estimators, SIAM J. Sci. Stat. Comput., 5
(1984), pp. 311-316.
-
49
-
S. HAMMARLING,
The numerical solution of the general Gauss-Markov
linear model, in Mathematics in Signal Processing,
eds. T. S. Durrani et al., Clarendon Press, Oxford
(1986).
-
50
-
N. J. HIGHAM, Efficient algorithms for computing the condition
number of a tridiagonal matrix, SIAM J. Sci. Stat. Comput., 7 (1986),
pp. 150-165.
-
51
-
N. J. HIGHAM, A survey of
condition number estimation for triangular matrices, SIAM Review, 29
(1987), pp. 575-596.
-
52
-
N. J. HIGHAM, FORTRAN codes for
estimating the one-norm of a real or complex matrix, with applications to
condition estimation, ACM Trans. Math. Soft., 14 (1988), pp. 381-396.
-
53
-
N. J. HIGHAM, Experience with a
matrix norm estimator, SIAM J. Sci. Stat. Comput., 11 (1990),
pp. 804-809.
-
54
-
N. J. HIGHAM, Perturbation Theory
and Backward Error for AX-XB=C., BIT, 33 (1993), pp. 124-136.
-
55
-
S. HUSS-LEDERMAN, A. TSAO AND G. ZHANG,
A parallel implementation of the invariant subspace
decomposition algorithm for dense symmetric matrices,
in Proceedings of the Sixth SIAM Conference on Parallel Processing for
Scientific Computing, SIAM (1993), pp. 367-374.
-
56
-
T. KATO, Perturbation Theory for Linear Operators, Springer Verlag,
Berlin, 2 ed., 1980.
-
57
-
L. KAUFMAN,
Banded eigenvalue solvers on vector machines,
ACM Trans. Math. Soft., 10 (1984), pp. 73-86.
-
58
-
C. L. LAWSON, R. J. HANSON, D. KINCAID, AND F. T. KROGH, Basic
Linear Algebra Subprograms for FORTRAN usage, ACM Trans. Math. Soft., 5
(1979), pp. 308-323.
-
59
-
R. LEHOUCQ, The computation of elementary unitary matrices,
Computer Science Dept. Technical Report CS-94-233, University
of Tennessee, Knoxville, 1994.
(LAPACK Working Note 72).
-
60
-
C. PAIGE,
Fast numerically stable computations for generalized linear least
squares problems,
SIAM J. Num. Anal., 16 (1979), pp. 165-179.
-
61
-
C. PAIGE,
A note on a result of Sun Ji-guang: sensitivity of the
CS and GSV decomposition,
SIAM J. Num. Anal., 21 (1984), pp. 186-191.
-
62
-
C. PAIGE,
Computing the generalized singular value decomposition,
SIAM J. Sci. Stat. Comput., 7 (1986), pp. 1126-1146.
-
63
-
C. PAIGE,
Some aspects of generalized QR factorization,
in Reliable Numerical Computations, eds. M. Cox and S. Hammarling,
Clarendon Press, Oxford (1990).
-
64
-
B. PARLETT, The Symmetric Eigenvalue Problem, Prentice Hall,
Englewood Cliffs, NJ, 1980.
-
65
-
M. PAYNE AND B. WICHMANN,
Language Independent Arithmetic (LIA) - Part 1:
Integer and floating point arithmetic,
International Standards Organization, ISO/IEC 10967-1:1994, 1994.
-
66
-
A. A. POLLICINI, ed., Using Toolpack Software Tools, Kluwer
Academic, 1989.
-
67
-
J. RUTTER,
A serial implementation of Cuppen's Divide and Conquer Algorithm for
the Symmetric Tridiagonal Eigenproblem,
University of California, Computer Science Division Report
UCB/CSD 94/799, Berkeley CA (1994).
(LAPACK Working Note 69).
-
68
-
R. SCHREIBER AND C. F. VAN LOAN, A storage efficient WY
representation for products of Householder transformations, SIAM J. Sci.
Stat. Comput., 10 (1989), pp. 53-57.
-
69
-
I. SLAPNICAR, Accurate symmetric eigenreduction by a
Jacobi method, PhD dissertation, Fernuniversität - Hagen,
Hagen, Germany, 1992.
-
70
-
B. T. SMITH, J. M. BOYLE, J. J. DONGARRA, B. S. GARBOW, Y. IKEBE, V. C.
KLEMA, AND C. B. MOLER, Matrix Eigensystem Routines - EISPACK
Guide, vol. 6 of Lecture Notes in Computer Science, Springer-Verlag, Berlin,
2 ed., 1976.
-
71
-
G. W. STEWART, On the sensitivity of the eigenvalue problem
 , SIAM J. Num. Anal., 9 (1972), pp. 669-686.
, SIAM J. Num. Anal., 9 (1972), pp. 669-686.
-
72
-
G. W. STEWART, Error and perturbation bounds for subspaces
associated with certain eigenvalue problems, SIAM Review, 15 (1973),
pp. 727-764.
-
73
-
G. W. STEWART AND J.-G. SUN, Matrix Perturbation Theory, Academic
Press, New York, 1990.
-
74
-
J.-G. SUN,
Perturbation analysis for the generalized singular value problem,
SIAM J. Num. Anal., 20 (1983), pp. 611-625.
-
75
-
J. VARAH, On the separation of two matrices, SIAM J. Num. Anal.,
16 (1979), pp. 216-222.
-
76
-
K. VESELIC AND I. SLAPNICAR,
Floating point perturbations of Hermitian matrices,
Linear Algebra Appl., to appear.
-
77
-
D. S. WATKINS AND L. ELSNER, Convergence of algorithms of
decomposition type for the eigenvalue problem, Linear Algebra Appl. 143 (1991),
pp. 19-47.
-
78
-
J. H. WILKINSON, The Algebraic Eigenvalue Problem, Oxford
University Press, Oxford, 1965.
-
79
-
J. H. WILKINSON,
Some recent advances in numerical linear algebra,
in: D. A. H. JACOBS, ed., The State of the Art in Numerical
Analysis, Academic Press, New York, 1977.
-
80
-
J. H. WILKINSON, Kronecker's canonical form and the QZ
algorithm, Lin. Alg. Appl., 28 (1979), pp. 285-303.
-
81
-
J. H. WILKINSON AND C. REINSCH, eds., Handbook for Automatic
Computation, vol 2.: Linear Algebra, Springer-Verlag, Heidelberg,
1971.
Tue Nov 29 14:03:33 EST 1994
Index




Next:
About this document
Up:
LAPACK Users' Guide Release
Previous:
References
- ####1####1
 Writing index file .idxK
Writing index file .idxK 
-
No Title
- ####1####1
 Writing index file .idxR
Writing index file .idxR 
-
No Title
- absolute error
-
How to Measure ,
How to Measure ,
How to Measure
- absolute gap
-
Further Details: Error ,
Further Details: Error ,
Further Details: Error ,
Further Details: Error
- accuracy
-
Accuracy and Stability,
Accuracy and Stability,
Further Details: Error ,
Further Details: Error
- accuracy!high
-
Accuracy and Stability,
Improved Error Bounds,
Further Details: Error ,
Further Details: Error ,
Further Details: Error ,
Further Details: Error
- angle between vectors and subspaces
-
How to Measure ,
How to Measure ,
How to Measure ,
Further Details: How ,
Further Details: How ,
Further Details: Error ,
Error Bounds for ,
Error Bounds for ,
Error Bounds for ,
Error Bounds for ,
Further Details: Error ,
Error Bounds for
- arguments!ABNRM
-
Balancing and Conditioning
- arguments!arrays
-
Array Arguments,
Array Arguments
- arguments!BALANC
-
Balancing and Conditioning
- arguments!BERR
-
Further Details: Error
- arguments!description conventions
-
Argument Descriptions
- arguments!DIAG
-
Unit Triangular Matrices
- arguments!dimensions
-
Problem Dimensions
- arguments!FERR
-
Error Bounds for ,
Further Details: Error
- arguments!ILO and IHI
-
Balancing,
Balancing and Conditioning
- arguments!INFO
-
Error Handling and ,
Invalid Arguments and ,
Computational Failures and
- arguments!LDA
-
Array Arguments,
Invalid Arguments and
- arguments!LWORK
-
Work Arrays
- arguments!options
-
Option Arguments
- arguments!order of
-
Order of Arguments
- arguments!RANK
-
Further Details: Error
- arguments!RCOND
-
How to Measure
- arguments!RCONDE
-
Overview,
Computing and
- arguments!RCONDV
-
Overview,
Computing and
- arguments!SCALE
-
Balancing and Conditioning
- arguments!UPLO
-
Option Arguments
- arguments!work space
-
Work Arrays
- ARPACK
-
Preface to the
- auxiliary routines
-
Levels of Routines
- Auxiliary Routines, index of: see Appendix B
-
Notes
- avoiding poor performance
-
Poor Performance
- backward error
-
Standard Error Analysis,
Standard Error Analysis,
Further Details: Error ,
Further Details: Error ,
Further Details: Error ,
Further Details: Error ,
Further Details: Error
- backward stability
-
Standard Error Analysis,
Overview,
Further Details: Error ,
Further Details: Error ,
Further Details: Error
- backward stability!componentwise
-
Improved Error Bounds,
Further Details: Error
- backward stability!normwise
-
Standard Error Analysis
- balancing and conditioning, eigenproblems
-
Generalized Nonsymmetric Eigenproblems
- balancing of eigenproblems
-
Balancing and Conditioning
- BANDR (EISPACK)
-
Notes
- BANDV (EISPACK)
-
Notes
- basis, orthonormal
-
Nonsymmetric Eigenproblems (NEP)
- bidiagonal
form
-
Eigenvalue Problems,
Representation of Orthogonal
- bidiagonal form
-
Singular Value Decomposition
- BLAS
-
LAPACK and the ,
The BLAS as
- BLAS!Level 1
-
The BLAS as
- BLAS!Level 2
-
The BLAS as ,
Block Algorithms and ,
Block Algorithms and
- BLAS!Level 3
-
The BLAS as ,
Block Algorithms and
- BLAS!Level 3, fast
-
Accuracy and Stability,
Error Bounds for
- BLAS!quick reference guide: see Appendix C
-
Quick Reference\indexBLAS!quick reference guide:
- block algorithm
-
Block Algorithms and
- block size
-
Installing ILAENV
- block size!determination of
-
Determining the Block
- block size!from ILAENV
-
Determining the Block
- block size!tuning ILAENV
-
Determining the Block
- block width
-
Block Algorithms and
- blocked algorithms, performance
-
Examples of Block
- BQR (EISPACK)
-
Notes
- bug reports
-
Support for LAPACK
- cache
-
Performance of LAPACK,
Data Movement
- CAPSS
-
Preface to the
- CBDSQR
-
Singular Value Decomposition,
Singular Value Decomposition,
Eigenvalue Problems,
Further Details: Error
- CGBBRD
-
Singular Value Decomposition
- CGBCON
-
Linear Equations
- CGBEQU
-
Linear Equations
- CGBRFS
-
Linear Equations
- CGBSVX
-
Further Details: How
- CGBTRF
-
Linear Equations
- CGBTRS
-
Linear Equations
- CGEBAK
-
Balancing
- CGEBAL
-
Balancing,
Balancing,
Balancing and Conditioning
- CGEBRD
-
Singular Value Decomposition
- CGECON
-
Linear Equations
- CGEEQU
-
Linear Equations
- CGEES
-
Nonsymmetric Eigenproblems (NEP),
Poor Performance
- CGEESX
-
Nonsymmetric Eigenproblems (NEP),
How to Measure ,
Overview,
Poor Performance
- CGEEV
-
Nonsymmetric Eigenproblems (NEP),
Poor Performance
- CGEEVX
-
Nonsymmetric Eigenproblems (NEP),
Error Bounds for ,
Overview,
Poor Performance
- CGEGS
-
Generalized Nonsymmetric Eigenproblems
- CGEGV
-
Generalized Nonsymmetric Eigenproblems
- CGEHRD
-
EigenvaluesEigenvectors and ,
Balancing,
Generalized Nonsymmetric Eigenproblems
- CGELQF
-
Factorization,
Singular Value Decomposition
- CGELS
-
Linear Least Squares ,
Error Bounds for ,
Further Details: Error
- CGELSS
-
Linear Least Squares ,
Linear Least Squares ,
Error Bounds for ,
Further Details: Error ,
Installing ILAENV
- CGELSX
-
Linear Least Squares ,
Linear Least Squares ,
Error Bounds for ,
Further Details: Error
- CGEQLF
-
Other Factorizations
- CGEQPF
-
Factorization with Column
- CGEQRF
-
Factorization,
Factorization with Column ,
Singular Value Decomposition
- CGERFS
-
Linear Equations
- CGERQF
-
Other Factorizations
- CGESVD
-
Singular Value Decomposition ,
Singular Value Decomposition,
Further Details: Error ,
Error Bounds for ,
Further Details: Error ,
Installing ILAENV
- CGESVX
-
Further Details: How
- CGETRF
-
Linear Equations
- CGETRI
-
Linear Equations
- CGETRS
-
Linear Equations
- CGGBAK
-
Generalized Nonsymmetric Eigenproblems,
Generalized Nonsymmetric Eigenproblems
- CGGBAL
-
Generalized Nonsymmetric Eigenproblems,
Generalized Nonsymmetric Eigenproblems
- CGGGLM
-
Generalized Linear Least
- CGGHRD
-
Generalized Nonsymmetric Eigenproblems
- CGGQRF
-
Generalized Factorization
- CGGRQF
-
Generalized factorization
- CGGSVD
-
Generalized Singular Value ,
Error Bounds for
- CGGSVP
-
Generalized (or Quotient)
- CGTCON
-
Linear Equations
- CGTRFS
-
Linear Equations
- CGTTRF
-
Linear Equations
- CGTTRS
-
Linear Equations
- CHBEV
-
Error Bounds for
- CHBEVD
-
Error Bounds for
- CHBEVX
-
Error Bounds for
- CHBGST
-
Generalized Symmetric Definite
- CHBGV
-
Error Bounds for
- CHBTRD
-
Symmetric Eigenproblems,
Symmetric Eigenproblems
- CHECON
-
Linear Equations
- CHEEV
-
Error Bounds for
- CHEEVD
-
Error Bounds for
- CHEEVX
-
Error Bounds for
- CHEGV
-
Standard Error Analysis,
Error Bounds for ,
Further Details: Error
- CHERFS
-
Linear Equations
- CHETRD
-
Symmetric Eigenproblems
- CHETRF
-
Linear Equations
- CHETRI
-
Linear Equations
- CHETRS
-
Linear Equations
- CHGEQZ
-
Generalized Nonsymmetric Eigenproblems
- Cholesky factorization!blocked form
-
Block Algorithms and
- Cholesky factorization!split
-
Generalized Symmetric Definite
- chordal distance
-
Further Details: Error
- CHPCON
-
Linear Equations
- CHPEV
-
Error Bounds for
- CHPEVD
-
Error Bounds for
- CHPEVX
-
Error Bounds for
- CHPGV
-
Error Bounds for
- CHPRFS
-
Linear Equations
- CHPTRD
-
Symmetric Eigenproblems
- CHPTRF
-
Linear Equations
- CHPTRI
-
Linear Equations
- CHPTRS
-
Linear Equations
- CHSEIN
-
EigenvaluesEigenvectors and
- CHSEQR
-
EigenvaluesEigenvectors and ,
Balancing,
Installing ILAENV,
Installing ILAENV,
Poor Performance
- cluster!eigenvalues
-
Further Details: Error
- cluster!eigenvalues!error bound
-
Overview
- cluster!singular values
-
Further Details: Error
- complete orthogonal factorization
-
Complete Orthogonal Factorization
- computational routines
-
Levels of Routines,
Computational Routines
- Computational Routines, index of: see Appendix A
-
Notes
- COMQR (EISPACK)
-
Eigenvalue Problems
- condensed form!reduction to
-
Eigenvalue Problems
- condition number
-
Invariant Subspaces and ,
Invariant Subspaces and ,
How to Measure ,
Standard Error Analysis,
Standard Error Analysis,
Error Bounds for ,
Error Bounds for ,
Further Details: Error ,
Further Details: Error ,
Error Bounds for ,
Error Bounds for ,
Error Bounds for ,
Overview,
Overview,
Balancing and Conditioning,
Balancing and Conditioning,
Balancing and Conditioning,
Error Bounds for ,
Error Bounds for ,
Further Details: Error ,
Error Bounds for
- condition number!estimate
-
Standard Error Analysis,
Further Details: Error ,
Computing and
- Cosine-Sine decomposition
-
Generalized Singular Value
- CPBCON
-
Linear Equations
- CPBEQU
-
Linear Equations
- CPBRFS
-
Linear Equations
- CPBSTF
-
Generalized Symmetric Definite
- CPBTRF
-
Linear Equations
- CPBTRS
-
Linear Equations
- CPOCON
-
Linear Equations
- CPOEQU
-
Linear Equations
- CPORFS
-
Linear Equations
- CPOTRF
-
Linear Equations
- CPOTRI
-
Linear Equations
- CPOTRS
-
Linear Equations
- CPPCON
-
Linear Equations
- CPPEQU
-
Linear Equations
- CPPRFS
-
Linear Equations
- CPPTRF
-
Linear Equations
- CPPTRI
-
Linear Equations
- CPPTRS
-
Linear Equations
- CPTCON
-
Linear Equations,
Further Details: Error
- CPTEQR
-
Symmetric Eigenproblems,
Further Details: Error
- CPTRFS
-
Linear Equations
- CPTTRF
-
Linear Equations
- CPTTRS
-
Linear Equations
- Crawford's algorithm
-
Generalized Symmetric Definite
- crossover point
-
Installing ILAENV
- CSPCON
-
Linear Equations
- CSPRFS
-
Linear Equations
- CSPTRF
-
Linear Equations
- CSPTRI
-
Linear Equations
- CSPTRS
-
Linear Equations
- CSTEDC
-
Symmetric Eigenproblems,
Eigenvalue Problems
- CSTEIN
-
Symmetric Eigenproblems,
Symmetric Eigenproblems
- CSTEQR
-
Symmetric Eigenproblems,
Symmetric Eigenproblems,
Eigenvalue Problems
- CSYCON
-
Linear Equations
- CSYRFS
-
Linear Equations
- CSYTRF
-
Linear Equations
- CSYTRI
-
Linear Equations
- CSYTRS
-
Linear Equations
- CTBCON
-
Linear Equations
- CTBRFS
-
Linear Equations
- CTBTRS
-
Linear Equations
- CTGEVC
-
Generalized Nonsymmetric Eigenproblems
- CTGSJA
-
Generalized (or Quotient) ,
Further Details: Error
- CTPCON
-
Linear Equations
- CTPRFS
-
Linear Equations
- CTPTRI
-
Linear Equations
- CTPTRS
-
Linear Equations
- CTRCON
-
Linear Equations,
Further Details: Error
- CTREVC
-
EigenvaluesEigenvectors and
- CTREXC
-
Invariant Subspaces and ,
Computing and
- CTRRFS
-
Linear Equations
- CTRSEN
-
Invariant Subspaces and ,
Overview
- CTRSNA
-
Invariant Subspaces and ,
Overview
- CTRSYL
-
Invariant Subspaces and ,
Computing and
- CTRTRI
-
Linear Equations
- CTRTRS
-
Linear Equations,
Factorization,
Factorization
- CTZRQF
-
Complete Orthogonal Factorization
- CUNGBR
-
Singular Value Decomposition
- CUNGHR
-
EigenvaluesEigenvectors and
- CUNGLQ
-
Factorization
- CUNGQR
-
Factorization,
Factorization with Column
- CUNMBR
-
Singular Value Decomposition
- CUNMHR
-
EigenvaluesEigenvectors and
- CUNMLQ
-
Factorization
- CUNMQR
-
Factorization,
Factorization,
Factorization,
Factorization with Column ,
Generalized Factorization,
Generalized factorization
- CUNMRQ
-
Generalized Factorization,
Generalized factorization
- CUNMTR
-
Symmetric Eigenproblems,
Symmetric Eigenproblems
- CUPGTR
-
Symmetric Eigenproblems
- Cuppen's divide and conquer algorithm
-
Symmetric Eigenproblems
- cycle time
-
Performance of LAPACK
- data movement
-
Data Movement
- DBDSQR
-
Singular Value Decomposition,
Singular Value Decomposition,
Eigenvalue Problems,
Further Details: Error
- DDISNA
-
Further Details: Error ,
Further Details: Error
- deflating subspaces
-
Generalized Nonsymmetric Eigenproblems ,
Generalized Nonsymmetric Eigenproblems
- deflating subspaces!error bound
-
Error Bounds for
- DGBBRD
-
Singular Value Decomposition
- DGBCON
-
Linear Equations
- DGBEQU
-
Linear Equations
- DGBRFS
-
Linear Equations
- DGBSVX
-
Further Details: How
- DGBTRF
-
Linear Equations
- DGBTRS
-
Linear Equations
- DGEBAK
-
Balancing
- DGEBAL
-
Balancing,
Balancing,
Balancing and Conditioning
- DGEBRD
-
Singular Value Decomposition
- DGECON
-
Linear Equations
- DGEEQU
-
Linear Equations
- DGEES
-
Nonsymmetric Eigenproblems (NEP),
Poor Performance
- DGEESX
-
Nonsymmetric Eigenproblems (NEP),
How to Measure ,
Overview,
Poor Performance
- DGEEV
-
Nonsymmetric Eigenproblems (NEP),
Poor Performance
- DGEEVX
-
Nonsymmetric Eigenproblems (NEP),
Error Bounds for ,
Overview,
Poor Performance
- DGEGS
-
Generalized Nonsymmetric Eigenproblems
- DGEGV
-
Generalized Nonsymmetric Eigenproblems
- DGEHRD
-
EigenvaluesEigenvectors and ,
Balancing,
Generalized Nonsymmetric Eigenproblems
- DGELQF
-
Factorization,
Singular Value Decomposition
- DGELS
-
Linear Least Squares ,
Error Bounds for ,
Further Details: Error
- DGELSS
-
Linear Least Squares ,
Linear Least Squares ,
Error Bounds for ,
Further Details: Error ,
Installing ILAENV
- DGELSX
-
Linear Least Squares ,
Linear Least Squares ,
Error Bounds for ,
Further Details: Error
- DGEQLF
-
Other Factorizations
- DGEQPF
-
Factorization with Column
- DGEQRF
-
Factorization,
Factorization with Column ,
Singular Value Decomposition,
Factorization
- DGERFS
-
Linear Equations
- DGERQF
-
Other Factorizations
- DGESVD
-
Singular Value Decomposition ,
Singular Value Decomposition,
Further Details: Error ,
Error Bounds for ,
Further Details: Error ,
Installing ILAENV
- DGESVX
-
Further Details: How
- DGETRF
-
Linear Equations,
Factorizations for Solving
- DGETRI
-
Linear Equations
- DGETRS
-
Linear Equations
- DGGBAK
-
Generalized Nonsymmetric Eigenproblems,
Generalized Nonsymmetric Eigenproblems
- DGGBAL
-
Generalized Nonsymmetric Eigenproblems,
Generalized Nonsymmetric Eigenproblems
- DGGGLM
-
Generalized Linear Least
- DGGHRD
-
Generalized Nonsymmetric Eigenproblems
- DGGQRF
-
Generalized Factorization
- DGGRQF
-
Generalized factorization
- DGGSVD
-
Generalized Singular Value ,
Error Bounds for
- DGGSVP
-
Generalized (or Quotient)
- DGTCON
-
Linear Equations
- DGTRFS
-
Linear Equations
- DGTTRF
-
Linear Equations
- DGTTRS
-
Linear Equations
- DHGEQZ
-
Generalized Nonsymmetric Eigenproblems
- DHSEIN
-
EigenvaluesEigenvectors and
- DHSEQR
-
EigenvaluesEigenvectors and ,
Balancing,
Installing ILAENV,
Installing ILAENV,
Poor Performance
- distributed memory
-
Preface to the
- divide and conquer
-
Symmetric Eigenproblems (SEP)
- DLAMCH
-
Sources of Error ,
Further Details: Floating ,
Points to Note
- documentation, structure
-
Structure of the
- DOPGTR
-
Symmetric Eigenproblems
- DOPMTR
-
Symmetric Eigenproblems
- DORGBR
-
Singular Value Decomposition
- DORGHR
-
EigenvaluesEigenvectors and
- DORGLQ
-
Factorization
- DORGQR
-
Factorization,
Factorization with Column
- DORGTR
-
Symmetric Eigenproblems
- DORMBR
-
Singular Value Decomposition,
Singular Value Decomposition
- DORMHR
-
EigenvaluesEigenvectors and ,
EigenvaluesEigenvectors and
- DORMLQ
-
Factorization,
Factorization
- DORMQR
-
Factorization,
Factorization,
Factorization,
Factorization with Column ,
Generalized Factorization,
Generalized factorization
- DORMRQ
-
Generalized Factorization,
Generalized factorization
- DORMTR
-
Symmetric Eigenproblems
- DPBCON
-
Linear Equations
- DPBEQU
-
Linear Equations
- DPBRFS
-
Linear Equations
- DPBSTF
-
Generalized Symmetric Definite
- DPBTRF
-
Linear Equations
- DPBTRS
-
Linear Equations
- DPOCON
-
Linear Equations
- DPOEQU
-
Linear Equations
- DPORFS
-
Linear Equations
- DPOTRF
-
Linear Equations,
Factorizations for Solving
- DPOTRI
-
Linear Equations
- DPOTRS
-
Linear Equations
- DPPCON
-
Linear Equations
- DPPEQU
-
Linear Equations
- DPPRFS
-
Linear Equations
- DPPTRF
-
Linear Equations
- DPPTRI
-
Linear Equations
- DPPTRS
-
Linear Equations
- DPTCON
-
Linear Equations,
Further Details: Error
- DPTEQR
-
Symmetric Eigenproblems,
Further Details: Error
- DPTRFS
-
Linear Equations
- DPTTRF
-
Linear Equations
- DPTTRS
-
Linear Equations
- driver routine!generalized least squares
-
Generalized Linear Least
- driver routine!generalized nonsymmetric eigenvalue problem
-
Generalized Nonsymmetric Eigenproblems ,
Generalized Nonsymmetric Eigenproblems
- driver routine!generalized SVD
-
Generalized Singular Value
- driver routine!generalized symmetric definite eigenvalue problem
-
Generalized Symmetric Definite
- driver routine!linear equations
-
Linear Equations
- driver routine!linear least squares
-
Linear Least Squares
- driver routine!nonsymmetric eigenvalue
problem
-
Nonsymmetric Eigenproblems (NEP)
- driver routine!SVD
-
Singular Value Decomposition
- driver routine!symmetric eigenvalue
problem
-
Symmetric Eigenproblems (SEP)
- driver routine!symmetric tridiagonal eigenvalue problem
-
Data Types and ,
Singular Value Decomposition
- driver routines
-
Levels of Routines,
Driver Routines
- driver routines!divide and conquer
-
Symmetric Eigenproblems (SEP)
- driver routines!expert
-
Linear Equations,
Symmetric Eigenproblems (SEP)
- driver routines!simple
-
Linear Equations,
Symmetric Eigenproblems (SEP)
- Driver Routines, index of: see
Appendix A
-
Notes
- DSBEV
-
Error Bounds for
- DSBEVD
-
Error Bounds for
- DSBEVX
-
Error Bounds for
- DSBGST
-
Generalized Symmetric Definite
- DSBGV
-
Error Bounds for
- DSBTRD
-
Symmetric Eigenproblems,
Symmetric Eigenproblems
- DSPCON
-
Linear Equations
- DSPEV
-
Error Bounds for
- DSPEVD
-
Error Bounds for
- DSPEVX
-
Error Bounds for
- DSPGV
-
Error Bounds for
- DSPRFS
-
Linear Equations
- DSPTRD
-
Symmetric Eigenproblems
- DSPTRF
-
Linear Equations
- DSPTRI
-
Linear Equations
- DSPTRS
-
Linear Equations
- DSTEBZ
-
Symmetric Eigenproblems,
Further Details: Error
- DSTEDC
-
Symmetric Eigenproblems,
Eigenvalue Problems
- DSTEIN
-
Symmetric Eigenproblems,
Symmetric Eigenproblems
- DSTEQR
-
Symmetric Eigenproblems,
Symmetric Eigenproblems,
Eigenvalue Problems
- DSTERF
-
Symmetric Eigenproblems,
Eigenvalue Problems
- DSTEV
-
Error Bounds for
- DSTEVD
-
Error Bounds for
- DSTEVX
-
Error Bounds for ,
Further Details: Error
- DSYCON
-
Linear Equations
- DSYEV
-
Error Bounds for
- DSYEVD
-
Error Bounds for
- DSYEVX
-
Error Bounds for
- DSYGV
-
Standard Error Analysis,
Error Bounds for ,
Further Details: Error
- DSYRFS
-
Linear Equations
- DSYTRD
-
Symmetric Eigenproblems,
Eigenvalue Problems
- DSYTRF
-
Linear Equations,
Factorizations for Solving
- DSYTRI
-
Linear Equations
- DSYTRS
-
Linear Equations
- DTBCON
-
Linear Equations
- DTBRFS
-
Linear Equations
- DTBTRS
-
Linear Equations
- DTGEVC
-
Generalized Nonsymmetric Eigenproblems
- DTGSJA
-
Generalized (or Quotient) ,
Further Details: Error
- DTPCON
-
Linear Equations
- DTPRFS
-
Linear Equations
- DTPTRI
-
Linear Equations
- DTPTRS
-
Linear Equations
- DTRCON
-
Linear Equations,
Further Details: Error
- DTREVC
-
EigenvaluesEigenvectors and
- DTREXC
-
Invariant Subspaces and ,
Computing and
- DTRRFS
-
Linear Equations
- DTRSEN
-
Invariant Subspaces and ,
Overview
- DTRSNA
-
Invariant Subspaces and ,
Overview
- DTRSYL
-
Invariant Subspaces and ,
Computing and
- DTRTRI
-
Linear Equations
- DTRTRS
-
Linear Equations,
Factorization,
Factorization
- DTZRQF
-
Complete Orthogonal Factorization
- effective rank
-
Factorization with Column
- efficiency
-
The BLAS as
- eigendecomposition!blocked form
-
Eigenvalue Problems
- eigendecomposition!multishift QR iteration
-
Eigenvalue Problems
- eigendecomposition!symmetric
-
Error Bounds for
- eigenvalue
-
Symmetric Eigenproblems (SEP),
Symmetric Eigenproblems (SEP),
Symmetric Eigenproblems,
EigenvaluesEigenvectors and ,
EigenvaluesEigenvectors and ,
Error Bounds for
- eigenvalue problem!ill-conditioned
-
Generalized Nonsymmetric Eigenproblems
- eigenvalue problem!singular
-
Generalized Nonsymmetric Eigenproblems
- eigenvalue!error bound
-
Error Bounds for ,
Further Details: Error ,
Error Bounds for ,
Overview,
Balancing and Conditioning,
Error Bounds for ,
Error Bounds for ,
Further Details: Error ,
Further Details: Error ,
Error Bounds for
- eigenvalue!generalized
-
Generalized Nonsymmetric Eigenproblems
- eigenvalue!GNEP
-
Generalized Nonsymmetric Eigenproblems
- eigenvalue!GSEP
-
Generalized Symmetric Definite
- eigenvalue!infinite
-
Generalized Nonsymmetric Eigenproblems
- eigenvalue!NEP
-
Nonsymmetric Eigenproblems (NEP)
- eigenvalue!nontrivial
-
Generalized Singular Value
- eigenvalue!ordering of
-
Nonsymmetric Eigenproblems (NEP),
Invariant Subspaces and
- eigenvalue!sensitivity of
-
Invariant Subspaces and ,
Invariant Subspaces and
- eigenvalue!SEP
-
Symmetric Eigenproblems
- eigenvalue!trivial
-
Generalized Singular Value
- eigenvector
-
Symmetric Eigenproblems (SEP),
Symmetric Eigenproblems,
Error Bounds for
- eigenvector!error bound
-
Error Bounds for ,
Further Details: Error ,
Error Bounds for ,
Overview,
Balancing and Conditioning,
Error Bounds for ,
Error Bounds for ,
Further Details: Error ,
Further Details: Error ,
Error Bounds for
- eigenvector!GNEP
-
Generalized Nonsymmetric Eigenproblems
- eigenvector!GNEP!left
-
Generalized Nonsymmetric Eigenproblems
- eigenvector!GNEP!right
-
Generalized Nonsymmetric Eigenproblems
- eigenvector!GSEP
-
Generalized Symmetric Definite
- eigenvector!left
-
Nonsymmetric Eigenproblems (NEP),
EigenvaluesEigenvectors and ,
Generalized Nonsymmetric Eigenproblems
- eigenvector!left!generalized
-
Generalized Nonsymmetric Eigenproblems
- eigenvector!NEP
-
Nonsymmetric Eigenproblems (NEP)
- eigenvector!right
-
Nonsymmetric Eigenproblems (NEP),
EigenvaluesEigenvectors and ,
Generalized Nonsymmetric Eigenproblems
- eigenvector!right!generalized
-
Generalized Nonsymmetric Eigenproblems
- eigenvector!SEP
-
Symmetric Eigenproblems
- EISPACK
-
LAPACK Compared with ,
Matrix Storage Schemes,
Band Storage,
Installing ILAENV
- EISPACK!converting from: see Appendix D
-
Converting from LINPACK
- elementary Householder matrix, see Householder matrix
-
Factorization,
Factorization,
Singular Value Decomposition,
Representation of Orthogonal ,
Representation of Orthogonal
- elementary reflector, see Householder matrix
-
Factorization,
Singular Value Decomposition,
Representation of Orthogonal ,
Representation of Orthogonal
- equality-constrained least squares
-
Generalized Linear Least
- equilibration
-
Linear Equations,
Linear Equations
- errata
-
Known Problems in
- error bounds
-
Accuracy and Stability
- error bounds!clustered eigenvalues
-
Overview
- error bounds!generalized least squares
-
Error Bounds for
- error bounds!generalized nonsymmetric eigenproblem
-
Error Bounds for
- error bounds!generalized singular value decomposition
-
Error Bounds for ,
Error Bounds for ,
Further Details: Error
- error bounds!generalized symmetric definite eigenproblem
-
Error Bounds for ,
Further Details: Error
- error bounds!linear equations
-
Error Bounds for ,
Further Details: Error
- error bounds!linear least squares
-
Error Bounds for ,
Further Details: Error
- error bounds!nonsymmetric eigenproblem
-
Error Bounds for ,
Overview
- error bounds!required for fast Level 3 BLAS
-
Error Bounds for
- error bounds!singular value decomposition
-
Error Bounds for ,
Further Details: Error
- error bounds!symmetric eigenproblem
-
Error Bounds for ,
Further Details: Error
- error handler, XERBLA
-
Error Handling and ,
Error Handling and ,
Invalid Arguments and
- error!absolute
-
How to Measure ,
How to Measure ,
How to Measure
- error!analysis
-
Standard Error Analysis
- error!backward
-
Standard Error Analysis,
Standard Error Analysis,
Further Details: Error ,
Further Details: Error ,
Further Details: Error ,
Further Details: Error ,
Further Details: Error
- error!measurement of
-
How to Measure
- error!measurement of!matrix
-
How to Measure ,
How to Measure
- error!measurement of!scalar
-
How to Measure ,
How to Measure
- error!measurement of!subspace
-
How to Measure ,
How to Measure
- error!measurement of!vector
-
How to Measure ,
How to Measure
- error!relative
-
Sources of Error ,
Further Details: Floating ,
How to Measure ,
How to Measure ,
How to Measure ,
Further Details: How ,
Standard Error Analysis,
Further Details: Error
- failures
-
Failures Detected by
- failures!common causes
-
Common Errors in
- failures!error handling
-
Error Handling and
- failures!INFO
-
Error Handling and
- floating-point arithmetic
-
Sources of Error
- floating-point arithmetic!guard digit
-
Further Details: Floating
- floating-point arithmetic!IEEE standard
-
Further Details: Floating
- floating-point arithmetic!infinity
-
Further Details: Floating
- floating-point arithmetic!machine precision
-
Sources of Error ,
Further Details: Floating
- floating-point arithmetic!NaN
-
Further Details: Floating
- floating-point arithmetic!Not-a-Number
-
Further Details: Floating
- floating-point arithmetic!overflow
-
Sources of Error ,
Further Details: Floating ,
Further Details: Floating ,
Further Details: Floating ,
How to Measure ,
Further Details: Error ,
Further Details: Error ,
Further Details: Error ,
Further Details: Error
- floating-point arithmetic!roundoff error
-
Further Details: Floating
- floating-point arithmetic!underflow
-
Sources of Error ,
Further Details: Floating ,
Further Details: Floating ,
Further Details: Floating
- forward error
-
Linear Equations
- forward stability
-
Improved Error Bounds
- forward stability!componentwise relative
-
Improved Error Bounds
- gap
-
Further Details: Error ,
Further Details: Error ,
Further Details: Error ,
Further Details: Error ,
Further Details: Error ,
Further Details: Error
- general linear model problem
-
Generalized Factorization
- generalized
eigenproblem!nonsymmetric
-
Generalized Nonsymmetric Eigenproblems
- generalized eigenproblem!symmetric definite
-
Generalized Symmetric Definite
- generalized eigenproblem!symmetric definite banded
-
Generalized Symmetric Definite
- generalized Hessenberg form!reduction to
-
Generalized Nonsymmetric Eigenproblems
- generalized least squares
-
Generalized Linear Least
- generalized orthogonal factorization
-
Generalized Orthogonal Factorizations
- generalized Schur vectors
-
Generalized Nonsymmetric Eigenproblems
- generalized singular value
-
Generalized Singular Value
- generalized singular value decomposition
-
Generalized Singular Value ,
Generalized (or Quotient)
- generalized singular value decomposition!special cases
-
Generalized Singular Value
- Givens rotation
-
Symmetric Eigenproblems,
Singular Value Decomposition,
Generalized Symmetric Definite
- GLM
-
Generalized Linear Least ,
Generalized Factorization
- GNEP
-
Generalized Nonsymmetric Eigenproblems
- GQR
-
Generalized Linear Least ,
Other Factorizations,
Generalized Factorization,
Generalized Factorization,
Generalized Factorization
- GRQ
-
Generalized Linear Least ,
Generalized factorization,
Generalized factorization
- GSEP
-
Generalized Symmetric Definite
- GSVD
-
Generalized Singular Value ,
Generalized Singular Value ,
Generalized (or Quotient)
- guard digit
-
Further Details: Floating
- Hessenberg
form
-
Eigenvalue Problems,
Eigenvalue Problems
- Hessenberg form
-
Balancing
- Hessenberg form!reduction to
-
Eigenvalue Problems
- Hessenberg form!upper
-
EigenvaluesEigenvectors and
- Householder matrix
-
Factorization,
Representation of Orthogonal
- Householder matrix!complex
-
Representation of Orthogonal
- Householder transformation - blocked form
-
Factorization
- Householder vector
-
Representation of Orthogonal
- HQR (EISPACK)
-
Eigenvalue Problems
- HTRID3 (EISPACK)
-
Notes
- HTRIDI (EISPACK)
-
Notes
- ILAENV
-
Determining the Block ,
Determining the Block ,
Points to Note,
Installing ILAENV,
Installing ILAENV,
Installing ILAENV,
Poor Performance
- ill-conditioned
-
Standard Error Analysis
- ill-posed
-
Standard Error Analysis
- IMTQL1 (EISPACK)
-
Notes
- IMTQL2 (EISPACK)
-
Notes
- infinity
-
Further Details: Floating
- input error
-
Sources of Error
- installation
-
Installation of LAPACK
- installation guide
-
Points to Note
- installation!ILAENV
-
Installing ILAENV
- installation!LAPACK
-
Points to Note
- installation!xLAMCH
-
Further Details: Floating ,
Points to Note
- installation!xLAMCH!cost of
-
Poor Performance
- invariant subspaces
-
Generalized Nonsymmetric Eigenproblems ,
Invariant Subspaces and ,
Overview
- invariant subspaces!error bound
-
Further Details: Error ,
Overview
- inverse
iteration
-
EigenvaluesEigenvectors and
- inverse iteration
-
Symmetric Eigenproblems
- iterative refinement
-
Linear Equations,
Error Bounds for
- LAPACK++
-
Preface to the
- LDL
 factorization
factorization -
Linear Equations
- linear equations
-
Linear Equations
- linear least
squares problem
-
Factorization with Column
- linear least squares
problem
-
Linear Least Squares ,
Orthogonal Factorizations and
- linear least squares problem
-
Factorization,
Factorization with Column
- linear least squares problem!generalized
-
Generalized Linear Least
- linear least squares problem!generalized!equality-constrained
(LSE)
-
Generalized factorization
- linear least squares problem!generalized!equality-constrained (LSE)
-
Generalized Linear Least
- linear least squares problem!generalized!regression model (GLM)
-
Generalized Linear Least
- linear least squares problem!overdetermined
-
Error Bounds for
- linear least squares problem!overdetermined system
-
Further Details: Error
- linear least squares problem!rank-deficient
-
Factorization with Column ,
Complete Orthogonal Factorization,
Singular Value Decomposition
- linear least squares problem!regularization
-
Further Details: Error
- linear least squares problem!underdetermined
-
Further Details: Error
- linear least squares problem!weighted
-
Generalized Linear Least
- linear systems, solution of
-
Linear Equations,
Linear Equations
- LINPACK
-
LAPACK Compared with ,
Block Algorithms and ,
Matrix Storage Schemes
- LINPACK!converting from: see Appendix D
-
Converting from LINPACK
- LLS
-
Linear Least Squares ,
Linear Least Squares
- local memory
-
Data Movement
- LQ factorization
-
Factorization
- LSE
-
Generalized Linear Least ,
Generalized Linear Least ,
Generalized factorization
- LU factorization
-
Linear Equations
- LU factorization!blocked form
-
Factorizations for Solving
- LU factorization!matrix types
-
Linear Equations
- machine parameters
-
Points to Note,
Installing ILAENV
- machine precision
-
Sources of Error ,
Further Details: Floating
- matrix inversion
-
Linear Equations
- minimum
norm solution
-
Linear Least Squares
- minimum norm
least squares solution
-
Linear Least Squares
- minimum norm
solution
-
Singular Value Decomposition
- minimum norm solution
-
Factorization,
Complete Orthogonal Factorization
- multishift QR algorithm, tuning
-
Installing ILAENV
- naming scheme
-
Naming Scheme
- naming scheme!auxiliary
-
Naming Scheme
- naming scheme!driver and
computational
-
Naming Scheme
- NaN
-
Further Details: Floating
- NEP
-
Nonsymmetric Eigenproblems (NEP)
- netlib
-
Availability of LAPACK
- nonsymmetric eigenproblem
-
EigenvaluesEigenvectors and
- nonsymmetric eigenproblem!generalized
-
Generalized Nonsymmetric Eigenproblems ,
Generalized Nonsymmetric Eigenproblems
- norm!Frobenius norm
-
Further Details: How
- norm!matrix
-
How to Measure
- norm!two norm
-
Further Details: How
- norm!vector
-
How to Measure
- normalization
-
Generalized Nonsymmetric Eigenproblems,
Generalized Nonsymmetric Eigenproblems
- Not-a-Number
-
Further Details: Floating
- Numerical Algorithms Group
-
Availability of LAPACK
- numerical error, sources of
-
Sources of Error
- numerical error, sources of!input error
-
Sources of Error
- numerical error, sources of!roundoff error
-
Sources of Error ,
Further Details: Floating
- orthogonal
(unitary) transformation
-
Complete Orthogonal Factorization
- orthogonal (unitary) factorizations
-
Orthogonal Factorizations and
- orthogonal (unitary) transformation
-
Generalized Nonsymmetric Eigenproblems,
Eigenvalue Problems
- orthogonal factorization!generalized
-
Generalized Orthogonal Factorizations
- overdetermined system
-
Linear Least Squares ,
Linear Least Squares ,
Further Details: Error ,
Further Details: Error
- overflow
-
Sources of Error ,
Further Details: Floating ,
Further Details: Floating ,
Further Details: Floating ,
How to Measure ,
Further Details: Error ,
Further Details: Error ,
Further Details: Error ,
Further Details: Error
- parallelism!compiler directives
-
Parallelism
- parallelism!loop-based
-
Parallelism
- PBLAS
-
ScaLAPACK
- pencils
-
Generalized Nonsymmetric Eigenproblems
- performance
-
Computers for which ,
Performance of LAPACK
- performance!block size
-
Installing ILAENV
- performance!crossover point
-
Installing ILAENV
- performance!LWORK
-
Poor Performance
- performance!recommendations
-
Poor Performance
- performance!sensitivity
-
Poor Performance
- permutation
-
Generalized Nonsymmetric Eigenproblems
- portability
-
Factors that Affect ,
The BLAS as ,
Further Details: Floating
- QL factorization
-
Other Factorizations
- QL factorization!implicit
-
Symmetric Eigenproblems
- QR decomposition!with pivoting
-
Generalized (or Quotient)
- QR factorization
-
Factorization
- QR factorization!blocked form
-
Factorization
- QR factorization!generalized (GQR)
-
Generalized Linear Least ,
Other Factorizations,
Generalized Factorization
- QR factorization!implicit
-
Symmetric Eigenproblems
- QR factorization!with pivoting
-
Factorization with Column
- quotient singular value decomposition
-
Generalized Singular Value ,
Generalized (or Quotient)
- QZ method
-
Generalized Nonsymmetric Eigenproblems
- rank!numerical determination of
-
Factorization with Column ,
Generalized (or Quotient) ,
Error Bounds for
- RATQR (EISPACK)
-
Notes
- reduction!bidiagonal
-
Singular Value Decomposition
- reduction!tridiagonal
-
Symmetric Eigenproblems,
Symmetric Eigenproblems
- reduction!upper Hessenberg
-
EigenvaluesEigenvectors and
- regression, generalized linear
-
Generalized Linear Least
- regularization
-
Further Details: Error
- relative error
-
Sources of Error ,
Further Details: Floating ,
How to Measure ,
How to Measure ,
How to Measure ,
Further Details: How ,
Standard Error Analysis,
Further Details: Error
- relative gap
-
Further Details: Error ,
Further Details: Error
- roundoff error
-
Sources of Error ,
Further Details: Floating
- RQ factorization
-
Other Factorizations
- RQ factorization!generalized (GRQ)
-
Generalized Linear Least ,
Generalized factorization,
Generalized factorization
- RSB (EISPACK)
-
Notes
- RST (EISPACK)
-
Notes
- s and sep
-
Computing and
- SBDSQR
-
Singular Value Decomposition,
Singular Value Decomposition,
Eigenvalue Problems,
Further Details: Error
- ScaLAPACK
-
ScaLAPACK
- scaling
-
Linear Equations,
Generalized Nonsymmetric Eigenproblems,
Balancing and Conditioning,
Balancing and Conditioning
- Schur
factorization!generalized
-
Generalized Nonsymmetric Eigenproblems
- Schur decomposition!generalized
-
Generalized Nonsymmetric Eigenproblems
- Schur factorization
-
Nonsymmetric Eigenproblems (NEP),
EigenvaluesEigenvectors and
- Schur factorization!generalized
-
Generalized Nonsymmetric Eigenproblems
- Schur form
-
EigenvaluesEigenvectors and ,
Balancing,
Invariant Subspaces and ,
Invariant Subspaces and
- Schur form!generalized
-
Generalized Nonsymmetric Eigenproblems,
Generalized Nonsymmetric Eigenproblems
- Schur vectors
-
Nonsymmetric Eigenproblems (NEP),
EigenvaluesEigenvectors and
- Schur vectors!generalized
-
Generalized Nonsymmetric Eigenproblems ,
Generalized Nonsymmetric Eigenproblems
- SDISNA
-
Further Details: Error ,
Further Details: Error
- SEP
-
Symmetric Eigenproblems (SEP),
Symmetric Eigenproblems
- separation of matrices
-
Computing and
- SGBBRD
-
Singular Value Decomposition
- SGBCON
-
Linear Equations
- SGBEQU
-
Linear Equations
- SGBRFS
-
Linear Equations
- SGBSVX
-
Further Details: How
- SGBTRF
-
Linear Equations
- SGBTRS
-
Linear Equations
- SGEBAK
-
Balancing
- SGEBAL
-
Balancing,
Balancing,
Balancing and Conditioning
- SGEBRD
-
Singular Value Decomposition,
Eigenvalue Problems,
Installing ILAENV
- SGECON
-
Linear Equations
- SGEEQU
-
Linear Equations
- SGEES
-
Nonsymmetric Eigenproblems (NEP),
Poor Performance
- SGEESX
-
Nonsymmetric Eigenproblems (NEP),
How to Measure ,
Overview,
Poor Performance
- SGEEV
-
Nonsymmetric Eigenproblems (NEP),
Poor Performance
- SGEEVX
-
Nonsymmetric Eigenproblems (NEP),
Error Bounds for ,
Overview,
Poor Performance
- SGEGS
-
Generalized Nonsymmetric Eigenproblems
- SGEGV
-
Generalized Nonsymmetric Eigenproblems
- SGEHRD
-
EigenvaluesEigenvectors and ,
Balancing,
Generalized Nonsymmetric Eigenproblems,
Eigenvalue Problems
- SGELQF
-
Factorization,
Singular Value Decomposition
- SGELS
-
Linear Least Squares ,
Error Bounds for ,
Further Details: Error
- SGELSS
-
Linear Least Squares ,
Linear Least Squares ,
Error Bounds for ,
Error Bounds for ,
Further Details: Error ,
Installing ILAENV
- SGELSX
-
Linear Least Squares ,
Linear Least Squares ,
Error Bounds for ,
Error Bounds for ,
Further Details: Error
- SGEQLF
-
Other Factorizations
- SGEQPF
-
Factorization with Column
- SGEQRF
-
Factorization,
Factorization with Column ,
Singular Value Decomposition,
Factorization,
Installing ILAENV,
Installing ILAENV
- SGERFS
-
Linear Equations
- SGERQF
-
Other Factorizations
- SGESV
-
Error Bounds for ,
Invalid Arguments and
- SGESVD
-
Singular Value Decomposition ,
Singular Value Decomposition,
Further Details: Error ,
Error Bounds for ,
Further Details: Error ,
Installing ILAENV
- SGESVX
-
Further Details: How ,
Error Bounds for ,
Computational Failures and ,
Computational Failures and
- SGETRF
-
Linear Equations,
Factorizations for Solving
- SGETRI
-
Linear Equations
- SGETRS
-
Linear Equations
- SGGBAK
-
Generalized Nonsymmetric Eigenproblems,
Generalized Nonsymmetric Eigenproblems
- SGGBAL
-
Generalized Nonsymmetric Eigenproblems,
Generalized Nonsymmetric Eigenproblems
- SGGGLM
-
Generalized Linear Least
- SGGHRD
-
Generalized Nonsymmetric Eigenproblems
- SGGQRF
-
Generalized Factorization
- SGGRQF
-
Generalized factorization
- SGGSVD
-
Generalized Singular Value ,
Error Bounds for
- SGGSVP
-
Generalized (or Quotient)
- SGTCON
-
Linear Equations
- SGTRFS
-
Linear Equations
- SGTTRF
-
Linear Equations
- SGTTRS
-
Linear Equations
- shared memory
-
Factors that Affect
- SHGEQZ
-
Generalized Nonsymmetric Eigenproblems
- SHSEIN
-
EigenvaluesEigenvectors and
- SHSEQR
-
EigenvaluesEigenvectors and ,
Balancing,
Installing ILAENV,
Installing ILAENV,
Poor Performance
- similarity transformation
-
Balancing
- singular value
-
Singular Value Decomposition
- singular value
decomposition (SVD)
-
Singular Value Decomposition
- singular value
decomposition!generalized
-
Generalized Singular Value
- singular value decomposition (SVD)
-
Singular Value Decomposition
- singular value decomposition!generalized
-
Generalized Singular Value ,
Generalized (or Quotient)
- singular value decomposition!generalized!special cases
-
Generalized Singular Value
- singular value!error bound
-
Error Bounds for ,
Further Details: Error ,
Further Details: Error ,
Error Bounds for ,
Further Details: Error
- singular value!generalized
-
Generalized Singular Value
- singular vector!error bound
-
Error Bounds for ,
Further Details: Error ,
Further Details: Error
- singular vectors!left
-
Singular Value Decomposition ,
Singular Value Decomposition
- singular vectors!right
-
Singular Value Decomposition ,
Singular Value Decomposition
- SLAMCH
-
Sources of Error ,
Further Details: Floating ,
Points to Note,
Poor Performance
- SOPGTR
-
Symmetric Eigenproblems
- SOPMTR
-
Symmetric Eigenproblems
- SORGBR
-
Singular Value Decomposition
- SORGHR
-
EigenvaluesEigenvectors and
- SORGLQ
-
Factorization
- SORGQR
-
Factorization,
Factorization with Column
- SORGTR
-
Symmetric Eigenproblems
- SORMBR
-
Singular Value Decomposition,
Singular Value Decomposition
- SORMHR
-
EigenvaluesEigenvectors and ,
EigenvaluesEigenvectors and
- SORMLQ
-
Factorization,
Factorization
- SORMQR
-
Factorization,
Factorization,
Factorization,
Factorization with Column ,
Generalized Factorization,
Generalized factorization
- SORMRQ
-
Generalized Factorization,
Generalized factorization
- SORMTR
-
Symmetric Eigenproblems
- source code
-
Availability of LAPACK
- SPBCON
-
Linear Equations
- SPBEQU
-
Linear Equations
- SPBRFS
-
Linear Equations
- SPBSTF
-
Generalized Symmetric Definite
- SPBTRF
-
Linear Equations
- SPBTRS
-
Linear Equations
- spectral factorization
-
Symmetric Eigenproblems (SEP)
- spectral projector
-
Computing and
- split Cholesky factorization
-
Generalized Symmetric Definite
- SPOCON
-
Linear Equations
- SPOEQU
-
Linear Equations
- SPOFA (LINPACK)
-
Block Algorithms and ,
Block Algorithms and
- SPORFS
-
Linear Equations
- SPOTRF
-
Linear Equations,
Block Algorithms and ,
Factorizations for Solving
- SPOTRI
-
Linear Equations
- SPOTRS
-
Linear Equations
- SPPCON
-
Linear Equations
- SPPEQU
-
Linear Equations
- SPPRFS
-
Linear Equations
- SPPTRF
-
Linear Equations
- SPPTRI
-
Linear Equations
- SPPTRS
-
Linear Equations
- SPTCON
-
Linear Equations,
Further Details: Error
- SPTEQR
-
Symmetric Eigenproblems,
Further Details: Error
- SPTRFS
-
Linear Equations
- SPTTRF
-
Linear Equations
- SPTTRS
-
Linear Equations
- SSBEV
-
Error Bounds for
- SSBEVD
-
Error Bounds for
- SSBEVX
-
Error Bounds for
- SSBGST
-
Generalized Symmetric Definite
- SSBGV
-
Error Bounds for
- SSBTRD
-
Symmetric Eigenproblems,
Symmetric Eigenproblems
- SSPCON
-
Linear Equations
- SSPEV
-
Error Bounds for
- SSPEVD
-
Error Bounds for
- SSPEVX
-
Error Bounds for
- SSPGV
-
Error Bounds for
- SSPRFS
-
Linear Equations
- SSPTRD
-
Symmetric Eigenproblems
- SSPTRF
-
Linear Equations
- SSPTRI
-
Linear Equations
- SSPTRS
-
Linear Equations
- SSTEBZ
-
Symmetric Eigenproblems,
Further Details: Error
- SSTEDC
-
Symmetric Eigenproblems,
Eigenvalue Problems
- SSTEIN
-
Symmetric Eigenproblems,
Symmetric Eigenproblems
- SSTEQR
-
Symmetric Eigenproblems,
Symmetric Eigenproblems,
Eigenvalue Problems
- SSTERF
-
Symmetric Eigenproblems,
Eigenvalue Problems
- SSTEV
-
Error Bounds for
- SSTEVD
-
Error Bounds for
- SSTEVX
-
Error Bounds for ,
Further Details: Error
- SSYCON
-
Linear Equations
- SSYEV
-
Error Bounds for
- SSYEVD
-
Error Bounds for
- SSYEVX
-
Error Bounds for
- SSYGV
-
Standard Error Analysis,
Error Bounds for ,
Further Details: Error
- SSYRFS
-
Linear Equations
- SSYTRD
-
Symmetric Eigenproblems,
Eigenvalue Problems,
Eigenvalue Problems
- SSYTRF
-
Linear Equations,
Factorizations for Solving ,
Factorizations for Solving
- SSYTRI
-
Linear Equations
- SSYTRS
-
Linear Equations
- stability
-
Orthogonal Factorizations and ,
Accuracy and Stability
- stability!backward
-
Standard Error Analysis,
Standard Error Analysis,
Improved Error Bounds,
Overview,
Further Details: Error ,
Further Details: Error ,
Further Details: Error ,
Further Details: Error
- stability!forward
-
Improved Error Bounds
- STBCON
-
Linear Equations
- STBRFS
-
Linear Equations
- STBTRS
-
Linear Equations
- STGEVC
-
Generalized Nonsymmetric Eigenproblems
- STGSJA
-
Generalized (or Quotient) ,
Further Details: Error
- storage scheme
-
Matrix Storage Schemes
- storage scheme!band
-
Band Storage
- storage scheme!band LU
-
Band Storage
- storage scheme!bidiagonal
-
Tridiagonal and Bidiagonal
- storage scheme!conventional
-
Conventional Storage
- storage scheme!diagonal of Hermitian matrix
-
Real Diagonal Elements
- storage scheme!Hermitian
-
Conventional Storage
- storage scheme!orthogonal or unitary matrices
-
Representation of Orthogonal
- storage scheme!packed
-
Packed Storage
- storage scheme!symmetric
-
Conventional Storage
- storage scheme!symmetric tridiagonal
-
Tridiagonal and Bidiagonal
- storage scheme!triangular
-
Conventional Storage
- storage scheme!unsymmetric tridiagonal
-
Tridiagonal and Bidiagonal
- STPCON
-
Linear Equations
- STPRFS
-
Linear Equations
- STPTRI
-
Linear Equations
- STPTRS
-
Linear Equations
- Strassen's method
-
Error Bounds for ,
Error Bounds for
- STRCON
-
Linear Equations,
Further Details: Error
- STREVC
-
EigenvaluesEigenvectors and
- STREXC
-
Invariant Subspaces and ,
Computing and
- STRRFS
-
Linear Equations
- STRSEN
-
Invariant Subspaces and ,
Overview
- STRSNA
-
Invariant Subspaces and ,
Overview
- STRSYL
-
Invariant Subspaces and ,
Computing and
- STRTRI
-
Linear Equations
- STRTRS
-
Linear Equations,
Factorization,
Factorization
- STZRQF
-
Complete Orthogonal Factorization
- subspaces
-
Further Details: How
- subspaces!angle between
-
How to Measure ,
How to Measure ,
How to Measure ,
Further Details: How ,
Further Details: How ,
Further Details: Error ,
Error Bounds for ,
Error Bounds for ,
Error Bounds for ,
Error Bounds for ,
Further Details: Error ,
Error Bounds for
- subspaces!deflating
-
Generalized Nonsymmetric Eigenproblems ,
Generalized Nonsymmetric Eigenproblems
- subspaces!invariant
-
Generalized Nonsymmetric Eigenproblems ,
Invariant Subspaces and
- support
-
Support for LAPACK
- SVD
-
Singular Value Decomposition
- Sylvester
equation
-
Standard Error Analysis,
Computing and ,
Computing and
- Sylvester equation
-
Invariant Subspaces and
- symmetric eigenproblem
-
Symmetric Eigenproblems
- symmetric indefinite factorization
-
Linear Equations
- symmetric indefinite factorization!blocked form
-
Factorizations for Solving
- TQL1 (EISPACK)
-
Notes
- TQL2 (EISPACK)
-
Notes
- TQLRAT (EISPACK)
-
Notes
- TRED1 (EISPACK)
-
Notes
- TRED2 (EISPACK)
-
Notes
- TRED3 (EISPACK)
-
Notes
- tridiagonal
form
-
Eigenvalue Problems
- tridiagonal form
-
Symmetric Eigenproblems,
Symmetric Eigenproblems,
Symmetric Eigenproblems,
Further Details: Error ,
Further Details: Error ,
Representation of Orthogonal
- troubleshooting
-
Troubleshooting
- tuning!block multishift QR: NS, MAXB
-
Installing ILAENV
- tuning!block size: NB, NBMIN, and NX
-
Installing ILAENV
- tuning!SVD: NXSVD
-
Installing ILAENV
- underdetermined system
-
Linear Least Squares ,
Linear Least Squares ,
Factorization,
Further Details: Error
- underflow
-
Sources of Error ,
Further Details: Floating ,
Further Details: Floating ,
Further Details: Floating
- upper Hessenberg form
-
EigenvaluesEigenvectors and
- vector registers
-
Data Movement
- vectorization
-
Vectorization
- workstation, super-scalar
-
Factors that Affect
- wrong results
-
Wrong Results
- XERBLA
-
Error Handling and ,
Invalid Arguments and ,
Invalid Arguments and
- xnetlib
-
Availability of LAPACK
- ZBDSQR
-
Singular Value Decomposition,
Singular Value Decomposition,
Eigenvalue Problems,
Further Details: Error
- ZGBBRD
-
Singular Value Decomposition
- ZGBCON
-
Linear Equations
- ZGBEQU
-
Linear Equations
- ZGBRFS
-
Linear Equations
- ZGBSVX
-
Further Details: How
- ZGBTRF
-
Linear Equations
- ZGBTRS
-
Linear Equations
- ZGEBAK
-
Balancing
- ZGEBAL
-
Balancing,
Balancing,
Balancing and Conditioning
- ZGEBRD
-
Singular Value Decomposition
- ZGECON
-
Linear Equations
- ZGEEQU
-
Linear Equations
- ZGEES
-
Nonsymmetric Eigenproblems (NEP),
Poor Performance
- ZGEESX
-
Nonsymmetric Eigenproblems (NEP),
How to Measure ,
Overview,
Poor Performance
- ZGEEV
-
Nonsymmetric Eigenproblems (NEP),
Poor Performance
- ZGEEVX
-
Nonsymmetric Eigenproblems (NEP),
Error Bounds for ,
Overview,
Poor Performance
- ZGEGS
-
Generalized Nonsymmetric Eigenproblems
- ZGEGV
-
Generalized Nonsymmetric Eigenproblems
- ZGEHRD
-
EigenvaluesEigenvectors and ,
Balancing,
Generalized Nonsymmetric Eigenproblems
- ZGELQF
-
Factorization,
Singular Value Decomposition
- ZGELS
-
Linear Least Squares ,
Error Bounds for ,
Further Details: Error
- ZGELSS
-
Linear Least Squares ,
Linear Least Squares ,
Error Bounds for ,
Further Details: Error ,
Installing ILAENV
- ZGELSX
-
Linear Least Squares ,
Linear Least Squares ,
Error Bounds for ,
Further Details: Error
- ZGEQLF
-
Other Factorizations
- ZGEQPF
-
Factorization with Column
- ZGEQRF
-
Factorization,
Factorization with Column ,
Singular Value Decomposition
- ZGERFS
-
Linear Equations
- ZGERQF
-
Other Factorizations
- ZGESVD
-
Singular Value Decomposition ,
Singular Value Decomposition,
Further Details: Error ,
Error Bounds for ,
Further Details: Error ,
Installing ILAENV
- ZGESVX
-
Further Details: How
- ZGETRF
-
Linear Equations
- ZGETRI
-
Linear Equations
- ZGETRS
-
Linear Equations
- ZGGBAK
-
Generalized Nonsymmetric Eigenproblems,
Generalized Nonsymmetric Eigenproblems
- ZGGBAL
-
Generalized Nonsymmetric Eigenproblems,
Generalized Nonsymmetric Eigenproblems
- ZGGGLM
-
Generalized Linear Least
- ZGGHRD
-
Generalized Nonsymmetric Eigenproblems
- ZGGQRF
-
Generalized Factorization
- ZGGRQF
-
Generalized factorization
- ZGGSVD
-
Generalized Singular Value ,
Error Bounds for
- ZGGSVP
-
Generalized (or Quotient)
- ZGTCON
-
Linear Equations
- ZGTRFS
-
Linear Equations
- ZGTTRF
-
Linear Equations
- ZGTTRS
-
Linear Equations
- ZHBEV
-
Error Bounds for
- ZHBEVD
-
Error Bounds for
- ZHBEVX
-
Error Bounds for
- ZHBGST
-
Generalized Symmetric Definite
- ZHBGV
-
Error Bounds for
- ZHBTRD
-
Symmetric Eigenproblems,
Symmetric Eigenproblems
- ZHECON
-
Linear Equations
- ZHEEV
-
Error Bounds for
- ZHEEVD
-
Error Bounds for
- ZHEEVX
-
Error Bounds for
- ZHEGV
-
Standard Error Analysis,
Error Bounds for ,
Further Details: Error
- ZHERFS
-
Linear Equations
- ZHETRD
-
Symmetric Eigenproblems
- ZHETRF
-
Linear Equations
- ZHETRI
-
Linear Equations
- ZHETRS
-
Linear Equations
- ZHGEQZ
-
Generalized Nonsymmetric Eigenproblems
- ZHPCON
-
Linear Equations
- ZHPEV
-
Error Bounds for
- ZHPEVD
-
Error Bounds for
- ZHPEVX
-
Error Bounds for
- ZHPGV
-
Error Bounds for
- ZHPRFS
-
Linear Equations
- ZHPTRD
-
Symmetric Eigenproblems
- ZHPTRF
-
Linear Equations
- ZHPTRI
-
Linear Equations
- ZHPTRS
-
Linear Equations
- ZHSEIN
-
EigenvaluesEigenvectors and
- ZHSEQR
-
EigenvaluesEigenvectors and ,
Balancing,
Installing ILAENV,
Installing ILAENV,
Poor Performance
- ZPBCON
-
Linear Equations
- ZPBEQU
-
Linear Equations
- ZPBRFS
-
Linear Equations
- ZPBSTF
-
Generalized Symmetric Definite
- ZPBTRF
-
Linear Equations
- ZPBTRS
-
Linear Equations
- ZPOCON
-
Linear Equations
- ZPOEQU
-
Linear Equations
- ZPORFS
-
Linear Equations
- ZPOTRF
-
Linear Equations
- ZPOTRI
-
Linear Equations
- ZPOTRS
-
Linear Equations
- ZPPCON
-
Linear Equations
- ZPPEQU
-
Linear Equations
- ZPPRFS
-
Linear Equations
- ZPPTRF
-
Linear Equations
- ZPPTRI
-
Linear Equations
- ZPPTRS
-
Linear Equations
- ZPTCON
-
Linear Equations,
Further Details: Error
- ZPTEQR
-
Symmetric Eigenproblems,
Further Details: Error
- ZPTRFS
-
Linear Equations
- ZPTTRF
-
Linear Equations
- ZPTTRS
-
Linear Equations
- ZSPCON
-
Linear Equations
- ZSPRFS
-
Linear Equations
- ZSPTRF
-
Linear Equations
- ZSPTRI
-
Linear Equations
- ZSPTRS
-
Linear Equations
- ZSTEDC
-
Symmetric Eigenproblems,
Eigenvalue Problems
- ZSTEIN
-
Symmetric Eigenproblems,
Symmetric Eigenproblems
- ZSTEQR
-
Symmetric Eigenproblems,
Symmetric Eigenproblems,
Eigenvalue Problems
- ZSYCON
-
Linear Equations
- ZSYRFS
-
Linear Equations
- ZSYTRF
-
Linear Equations
- ZSYTRI
-
Linear Equations
- ZSYTRS
-
Linear Equations
- ZTBCON
-
Linear Equations
- ZTBRFS
-
Linear Equations
- ZTBTRS
-
Linear Equations
- ZTGEVC
-
Generalized Nonsymmetric Eigenproblems
- ZTGSJA
-
Generalized (or Quotient) ,
Further Details: Error
- ZTPCON
-
Linear Equations
- ZTPRFS
-
Linear Equations
- ZTPTRI
-
Linear Equations
- ZTPTRS
-
Linear Equations
- ZTRCON
-
Linear Equations,
Further Details: Error
- ZTREVC
-
EigenvaluesEigenvectors and
- ZTREXC
-
Invariant Subspaces and ,
Computing and
- ZTRRFS
-
Linear Equations
- ZTRSEN
-
Invariant Subspaces and ,
Overview
- ZTRSNA
-
Invariant Subspaces and ,
Overview
- ZTRSYL
-
Invariant Subspaces and ,
Computing and
- ZTRTRI
-
Linear Equations
- ZTRTRS
-
Linear Equations,
Factorization,
Factorization
- ZTZRQF
-
Complete Orthogonal Factorization
- ZUNGBR
-
Singular Value Decomposition
- ZUNGHR
-
EigenvaluesEigenvectors and
- ZUNGLQ
-
Factorization
- ZUNGQR
-
Factorization,
Factorization with Column
- ZUNMBR
-
Singular Value Decomposition
- ZUNMHR
-
EigenvaluesEigenvectors and
- ZUNMLQ
-
Factorization
- ZUNMQR
-
Factorization,
Factorization,
Factorization,
Factorization with Column ,
Generalized Factorization,
Generalized factorization
- ZUNMRQ
-
Generalized Factorization,
Generalized factorization
- ZUNMTR
-
Symmetric Eigenproblems,
Symmetric Eigenproblems
- ZUPGTR
-
Symmetric Eigenproblems
Tue Nov 29 14:03:33 EST 1994
Installation of LAPACK





Next:
Support for LAPACK
Up:
Essentials
Previous:
Availability of LAPACK
A Quick Installation Guide (LAPACK Working Note 81)
[35] is
distributed with the complete package. This Quick Installation Guide
provides installation instructions for Unix Systems. A comprehensive
Installation Guide
[3] (LAPACK Working Note 41), which contains
descriptions of the testing and timings programs, as well as detailed non-Unix
installation instructions, is also available.
See also Chapter
6.
Tue Nov 29 14:03:33 EST 1994
<em>About this document ...</em>





Up:
LAPACK Users' Guide Release
Previous:
Index
LAPACK Users' Guide
Release 2.0
This document was generated using the
LaTeX2HTML translator Version 0.6.4 (Tues Aug 30 1994) Copyright © 1993, 1994,
Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html lapack_lug.tex.
The translation was initiated by on Tue Nov 29 14:03:33 EST 1994
Tue Nov 29 14:03:33 EST 1994
Support for LAPACK





Next:
Known Problems in
Up:
Essentials
Previous:
Installation of LAPACK
LAPACK has been thoroughly tested before release, on many different
types of computers.
The LAPACK project supports the package in the sense that reports
of errors or poor performance will gain immediate attention from the
developers
.
Such reports - and also descriptions of interesting
applications and other comments - should be sent to:
LAPACK Project
c/o J. J. Dongarra
Computer Science Department
University of Tennessee
Knoxville, TN 37996-1301
USA
Email: lapack@cs.utk.edu
Tue Nov 29 14:03:33 EST 1994
Known Problems in LAPACK





Next:
Other Related Software
Up:
Essentials
Previous:
Support for LAPACK
A list of known problems, bugs, and compiler errors
for LAPACK,
as well as an errata list for this guide, is maintained on netlib.
For a copy of this report, send email to netlib of the form:
send release_notes from lapack
Tue Nov 29 14:03:33 EST 1994
Other Related Software





Next:
LAPACK++
Up:
Essentials
Previous:
Known Problems in
As previously mentioned in the Preface, many LAPACK-related software
projects are currently available on netlib. In the context of this
users' guide, several of these projects require further discussion - LAPACK++,
CLAPACK, ScaLAPACK, and LAPACK routines exploiting IEEE arithmetic.
Tue Nov 29 14:03:33 EST 1994
LAPACK++





Next:
CLAPACK
Up:
Other Related Software
Previous:
Other Related Software
LAPACK++ is an object-oriented C++ extension to the LAPACK library.
Traditionally, linear algebra libraries have been available only in
Fortran. However, with an increasing number of programmers using C and C++
for scientific software development, there is a need to have
high-quality numerical libraries to support these platforms as well.
LAPACK++ provides the speed and efficiency competitive with native
Fortran codes, while allowing programmers to capitalize on the software
engineering benefits of object-oriented programming.
LAPACK++ supports various matrix classes for vectors, non-symmetric
matrices, symmetric positive definite matrices, symmetric matrices, banded,
triangular, and tridiagonal matrices; however, the current version does not
include all of the capabilities of original Fortran 77 LAPACK. Emphasis is
given to routines for solving linear systems consisting of nonsymmetric
matrices, symmetric positive definite systems, and solving linear least-square
systems. Future versions of LAPACK++
will support eigenvalue problems and singular value decompositions as
well as distributed matrix classes for parallel computer architectures.
For a more detailed description of the design of LAPACK++, please see
[36]. This paper, as well as an Installation manual and Users'
Guide are available on netlib. To obtain this software or documentation
send a message to netlib@ornl.gov of the form:
send index from c++/lapack++
Questions and comments about LAPACK++ can be directed to lapackpp@cs.utk.edu.
Tue Nov 29 14:03:33 EST 1994
CLAPACK





Next:
ScaLAPACK
Up:
Other Related Software
Previous:
LAPACK++
The CLAPACK library was built using a Fortran to C conversion utility
called f2c
[40].
The entire Fortran 77 LAPACK library is run
through f2c to obtain C code, and then modified to
improve readability. CLAPACK's goal is to provide
LAPACK for someone who does not have access to a Fortran compiler.
However, f2c is designed to create C code that is still callable from
Fortran, so all arguments must be passed using Fortran calling
conventions and data structures.
This requirement has several repercussions.
The first is that since many compilers require distinct Fortran and C routine
namespaces, an underscore (_) is appended to C routine names
which will be called from Fortran.
Therefore, f2c has added this underscore to all the names in CLAPACK.
So, a call that in Fortran would look like:
call dgetrf(...)
becomes in C:
dgetrf_(...);
Second, the user must pass ALL arguments by reference, i.e. as pointers,
since this is how Fortran works. This includes all scalar arguments
like M and N. This restriction means that you cannot make a
call with numbers directly in the parameter sequence. For example,
consider the LU factorization of a 5-by-5 matrix. If the matrix to
be factored is called A, the Fortran call
call dgetrf(5, 5, A, 5, ipiv, info)
becomes in C:
M = N = LDA = 5;
dgetrf_(&M, &N, A, &LDA, ipiv, &info);
Some LAPACK routines take character string arguments. In all but the
testing and timing code, only the first character of the string is
signficant. Therefore, the CLAPACK driver, computational, and auxiliary
routines only expect single character arguments. For example, the Fortran
call
call dpotrf( 'Upper', n, a, lda, info )
becomes in C:
char s = 'U';
dpotrf_(&s, &n, a, &lda, &info);
In a future release we hope to provide ``wrapper'' routines that will
remove the need for these unnecessary pointers, and automatically
allocate (``malloc'') any workspace that is required.
As a final point, we must stress that there is a difference in the definition
of a two-dimensional array in Fortran and C.
A two-dimensional Fortran array declared as
DOUBLE PRECISION A(LDA, N)
is a contiguous piece of LDA N double-words of memory,
stored in column-major order: elements in a column are
contiguous, and elements within a row are separated by a stride of LDA
double-words.
N double-words of memory,
stored in column-major order: elements in a column are
contiguous, and elements within a row are separated by a stride of LDA
double-words.
In C, however, a two-dimensional array is in row-major order. Further, the
rows of a two-dimensional C array need not be contiguous. The array
double A[LDA][N];
actually has LDA pointers to rows of length N.
These pointers can in
principle be anywhere in memory. Passing such a two-dimensional C
array to a CLAPACK routine will almost surely give erroneous results.
Instead, you must use a one-dimensional C array of size LDA N
double-words (or else malloc the same amount of space).
We recommend using the following code to get the array CLAPACK will be
expecting:
N
double-words (or else malloc the same amount of space).
We recommend using the following code to get the array CLAPACK will be
expecting:
double *A;
A = malloc( LDA*N*sizeof(double) );
Note that for best memory utilization, you would set LDA=M, the
actual number of rows of A. If you now
wish to operate on the matrix A, remember that A is in column-major
order. As an example of accessing Fortran-style arrays in C, the following
code fragments show how to initialize the array A declared above
so that
all of column  has the value
has the value  :
:
double *ptr;
ptr = A;
for(j=0; j < N; j++)
{
for (i=0; i < M; i++) *ptr++ = j;
ptr += (LDA - M);
}
or, you can use:
for(j=0; j < N; j++)
{
for (i=0; i < M; i++) A[j*LDA+i] = j;
}
Note that the loop over the row index i is the inner loop, since column
entries are contiguous.





Next:
ScaLAPACK
Up:
Other Related Software
Previous:
LAPACK++
Tue Nov 29 14:03:33 EST 1994
List of Tables





Next:
Preface to the
Up:
LAPACK Users' Guide Release
Previous:
Contents
-
Matrix types in the LAPACK naming scheme
-
Driver routines for linear equations
-
Driver routines for linear least squares problems
-
Driver routines for generalized linear least squares problems
-
Driver routines for standard eigenvalue and singular value problems
-
Driver routines for generalized eigenvalue and singular value problems
-
Computational routines for linear equations
-
Computational routines for linear equations (continued)
-
Computational routines for orthogonal factorizations
-
Computational routines for the symmetric eigenproblem
-
Computational routines for the nonsymmetric eigenproblem
-
Computational routines for the singular value decomposition
-
Reduction of generalized symmetric definite eigenproblems to standard
problems
-
Computational routines for the generalized symmetric definite eigenproblem
-
Computational routines for the generalized nonsymmetric eigenproblem
-
Computational routines for the generalized singular value decomposition
-
Speed in megaflops of Level 2 and Level 3 BLAS operations on a
CRAY C90
-
Clock Speeds of Computers in Timing Results
-
Speed in megaflops of SGETRF/DGETRF for square matrices of order n
-
Speed in megaflops of SPOTRF/DPOTRF for matrices of order n with UPLO = `U'
-
Speed in megaflops of DSYTRF for matrices of order n with UPLO = `U' on an IBM POWER2 model 590
-
Speed in megaflops of SGEQRF/DGEQRF for square matrices of order n
-
Speed in megaflops of reductions to condensed forms on an IBM POWER2 model 590
-
Execution time and Megaflop rates for SGEMV/DGEMV and
SGEMM/DGEMM
-
``Standard'' floating point operation counts for LAPACK drivers
for n-by-n matrices
-
Performance of SGESV/DGESV for n-by-n matrices
-
Performance of SGELS/DGELS for n-by-n matrices
-
Performance of SGEEV/DGEEV, eigenvalues only
-
Performance of SGEEV/DGEEV, eigenvalues and right eigenvectors
-
Performance of SSYEVD/DSYEVD, eigenvalues only, UPLO='U'
-
Performance of SSYEVD/DSYEVD, eigenvalues and eigenvectors, UPLO='U'
-
Performance of SGESVD/DGESVD, singular values only
-
Performance of SGESVD/DGESVD, singular values and left and right singular vectors
-
Values of Machine Parameters in IEEE Floating Point Arithmetic
-
Vector and matrix norms
-
Bounding One Vector Norm in Terms of Another
-
Bounding One Matrix Norm in Terms of Another
-
Asymptotic error bounds for the nonsymmetric eigenproblem
-
Global error bounds for the nonsymmetric eigenproblem
assuming

-
Use of the block parameters NB, NBMIN, and NX in LAPACK
Tue Nov 29 14:03:33 EST 1994
ScaLAPACK





Next:
LAPACK routines exploiting
Up:
Other Related Software
Previous:
CLAPACK
The ScaLAPACK (or Scalable LAPACK)
library includes
a subset of LAPACK routines redesigned for distributed memory parallel
computers. It is currently written in a Single-Program-Multiple-Data style using
explicit message passing for interprocessor communication. It assumes
matrices are laid out in
a two-dimensional block cyclic decomposition.
The goal is to have ScaLAPACK routines resemble their LAPACK
equivalents as much as possible. Just as LAPACK
is built on top of the BLAS, ScaLAPACK relies on the PBLAS
(Parallel Basic Linear Algebra Subprograms)
and the
BLACS (Basic Linear Algebra Communication Subprograms).
The PBLAS perform computations analogous to the BLAS but on matrices
distributed across multiple processors.
The PBLAS rely on the communication protocols of the BLACS.
The BLACS are designed for linear
algebra applications and provide portable communication across a wide variety
of distributed-memory architectures. At
the present time, they are available for the Intel Gamma, Delta, and Paragon,
Thinking Machines CM-5, IBM SPs, and PVM. They will soon be available
for the CRAY T3D. For more information:
echo ''send index from scalapack'' | mail netlib@ornl.gov
All questions/comments can be directed to scalapack@cs.utk.edu.
Tue Nov 29 14:03:33 EST 1994
LAPACK routines exploiting IEEE arithmetic





Next:
Contents of LAPACK
Up:
Other Related Software
Previous:
ScaLAPACK
We have also explored the advantages of IEEE arithmetic in
implementing linear algebra routines. For example, the accurate rounding
properties of IEEE arithmetic permit high precision arithmetic to be
simulated economically in short stretches of code, thereby replacing
possibly much more complicated low precision algorithms. Second, the
``friendly'' exception handling capabilities of IEEE arithmetic, such as
being able to continue computing past an overflow and to ask later whether
an overflow occurred, permit us to use simple, fast algorithms which work
almost all the time, and revert to slower, safer algorithms only if the fast
algorithm fails. See
[23] for more details.
However, the continuing importance of machines implementing Cray arithmetic,
the existence of some machines that only implement full IEEE exception
handling by slowing down all floating point operations significantly,
and the lack of portable ways to refer to
exceptions in Fortran or C, has led us not to include these improved
algorithms in this release of
LAPACK. Since Cray has announced plans to convert to IEEE arithmetic, and
some progress is being made on standardizing exception
handling
[65]
we do expect to make these routines available in a future release.
Tue Nov 29 14:03:33 EST 1994
Contents of LAPACK





Next:
Structure of LAPACK
Up:
Guide
Previous:
LAPACK routines exploiting
Tue Nov 29 14:03:33 EST 1994
Structure of LAPACK





Next:
Levels of Routines
Up:
Contents of LAPACK
Previous:
Contents of LAPACK
Tue Nov 29 14:03:33 EST 1994
Levels of Routines





Next:
Data Types and
Up:
Structure of LAPACK
Previous:
Structure of LAPACK
The subroutines in LAPACK are classified as follows:
- driver routines
, each of which solves a complete problem,
for example solving a system of linear equations, or computing the
eigenvalues of a real symmetric matrix.
Users are recommended to use a driver routine if there is one that
meets their requirements. They are listed in Section
2.2.
- computational routines
, each of which performs a distinct
computational task, for example an LU factorization,
or the reduction of a real symmetric matrix to tridiagonal form.
Each driver routine calls a
sequence of computational routines. Users (especially software developers)
may need to call
computational routines directly to perform tasks, or sequences of tasks,
that cannot conveniently
be performed by the driver routines. They are listed in
Section
2.3.
- auxiliary routines
, which in turn can be classified as follows:
- routines that perform subtasks of block algorithms - in particular,
routines that implement unblocked versions of the algorithms;
- routines that perform some commonly required low-level
computations, for example scaling a matrix, computing a matrix-norm,
or generating an elementary Householder matrix; some of
these may be of interest to numerical analysts or software developers and
could be considered for future additions to the BLAS;
- a few extensions to the BLAS, such as routines for applying complex plane
rotations, or matrix-vector operations involving complex symmetric
matrices (the BLAS themselves are not strictly speaking part of LAPACK).
Both driver routines and computational routines are fully described in
this Users' Guide, but not the auxiliary routines.
A list of the auxiliary routines, with brief descriptions
of their functions, is given in Appendix
B.
Tue Nov 29 14:03:33 EST 1994
Data Types and Precision





Next:
Naming Scheme
Up:
Structure of LAPACK
Previous:
Levels of Routines
LAPACK provides the same range of functionality for real
and complex data.
For most computations there are matching
routines, one for real and one for complex data,
but there are a few exceptions. For example, corresponding to the routines
for real symmetric indefinite systems of linear equations, there are
routines for complex Hermitian and complex symmetric systems,
because both types of complex systems occur in practical applications.
However, there is no complex analogue of the routine for finding
selected eigenvalues of a real symmetric tridiagonal matrix,
because a complex Hermitian matrix can always be reduced to
a real symmetric tridiagonal matrix.
Matching routines for real and complex data have been coded
to maintain a close correspondence between the two, wherever possible.
However, in some areas (especially the nonsymmetric eigenproblem) the
correspondence is necessarily weaker.
All routines in LAPACK are provided in both single and
double precision versions. The double precision versions have
been generated automatically, using Toolpack/1
[66].
Double precision routines for complex matrices require the
non-standard Fortran data type COMPLEX*16, which is available on
most machines where double precision computation is usual.
Tue Nov 29 14:03:33 EST 1994
Naming Scheme





Next:
Driver Routines
Up:
Structure of LAPACK
Previous:
Data Types and
The name of each LAPACK routine is a coded specification of
its function (within the very tight limits of standard Fortran 77
6-character names).
All driver and computational routines
have names
of the form XYYZZZ, where for
some driver routines the 6th character is blank.
The first letter, X, indicates the data type as follows:
S REAL
D DOUBLE PRECISION
C COMPLEX
Z COMPLEX*16 or DOUBLE COMPLEX
When we wish to refer to an LAPACK routine generically, regardless
of data type, we replace the first letter by ``x''. Thus xGESV refers
to any or all of the routines SGESV, CGESV, DGESV and ZGESV.
The next two letters, YY, indicate the type of matrix (or
of the most significant matrix).
Most of these two-letter codes apply to both real and complex matrices;
a few apply specifically to one or the other, as indicated in Table
2.1.
BD bidiagonal
GB general band
GE general (i.e., unsymmetric, in some cases rectangular)
GG general matrices, generalized problem (i.e., a pair of general
matrices) (not used in Release 1.0)
GT general tridiagonal
HB (complex) Hermitian band
HE (complex) Hermitian
HG upper Hessenberg matrix, generalized problem (i.e a Hessenberg and
a triangular matrix) (not used in Release 1.0)
HP (complex) Hermitian, packed storage
HS upper Hessenberg
OP (real) orthogonal, packed storage
OR (real) orthogonal
PB symmetric or Hermitian positive definite band
PO symmetric or Hermitian positive definite
PP symmetric or Hermitian positive definite, packed storage
PT symmetric or Hermitian positive definite tridiagonal
SB (real) symmetric band
SP symmetric, packed storage
ST (real) symmetric tridiagonal
SY symmetric
TB triangular band
TG triangular matrices, generalized problem (i.e., a pair of triangular
matrices) (not used in Release 1.0)
TP triangular, packed storage
TR triangular (or in some cases quasi-triangular)
TZ trapezoidal
UN (complex) unitary
UP (complex) unitary, packed storage
Table 2.1: Matrix types in the LAPACK naming scheme
When we wish to refer to a class of routines that performs the
same function on different types of matrices, we replace the first three
letters by ``xyy''. Thus xyySVX refers to all the expert driver routines for
systems of linear equations that are listed in Table
2.2.
The last three letters ZZZ indicate the computation performed.
Their meanings will be explained in Section
2.3.
For example, SGEBRD is a single precision routine that performs a
bidiagonal reduction (BRD) of a real general matrix.
The names of auxiliary routines
follow a
similar scheme except that the
2nd and 3rd characters YY are usually LA (for example, SLASCL
or CLARFG). There are two kinds of exception.
Auxiliary routines that implement an unblocked version of a block
algorithm have similar names to the routines that perform
the block algorithm, with the sixth character being ``2'' (for example,
SGETF2 is the unblocked version of SGETRF).
A few routines that may be
regarded as extensions to the BLAS are named according to the BLAS
naming schemes (for example, CROT, CSYR).





Next:
Driver Routines
Up:
Structure of LAPACK
Previous:
Data Types and
Tue Nov 29 14:03:33 EST 1994
Driver Routines





Next:
Linear Equations
Up:
Contents of LAPACK
Previous:
Naming Scheme
This section describes the driver routines
in LAPACK. Further details on
the terminology and the numerical operations they perform
are given in
Section
2.3, which describes the computational routines.
Tue Nov 29 14:03:33 EST 1994
Linear Equations





Next:
Linear Least Squares
Up:
Driver Routines
Previous:
Driver Routines
Two types of driver routines are provided for solving systems of linear
equations
:
Both types of driver routines can handle multiple right hand sides
(the columns of B).
Different driver routines are provided to take advantage of special
properties or storage schemes of the matrix A, as shown in
Table
2.2.
These driver routines cover all the functionality of the computational
routines for linear systems
, except matrix
inversion
. It is seldom
necessary to compute the inverse of a matrix explicitly, and it is
certainly not recommended as a means of solving linear systems.
--------------------------------------------------------------------------
Type of matrix Single precision Double precision
and storage scheme Operation real complex real complex
--------------------------------------------------------------------------
general simple driver SGESV CGESV DGESV ZGESV
expert driver SGESVX CGESVX DGESVX ZGESVX
--------------------------------------------------------------------------
general band simple driver SGBSV CGBSV DGBSV ZGBSV
expert driver SGBSVX CGBSVX DGBSVX ZGBSVX
--------------------------------------------------------------------------
general tridiagonal simple driver SGTSV CGTSV DGTSV ZGTSV
expert driver SGTSVX CGTSVX DGTSVX ZGTSVX
--------------------------------------------------------------------------
symmetric/Hermitian simple driver SPOSV CPOSV DPOSV ZPOSV
positive definite expert driver SPOSVX CPOSVX DPOSVX ZPOSVX
--------------------------------------------------------------------------
symmetric/Hermitian simple driver SPPSV CPPSV DPPSV ZPPSV
positive definite expert driver SPPSVX CPPSVX DPPSVX ZPPSVX
(packed storage)
--------------------------------------------------------------------------
symmetric/Hermitian simple driver SPBSV CPBSV DPBSV ZPBSV
positive definite expert driver SPBSVX CPBSVX DPBSVX ZPBSVX
band
--------------------------------------------------------------------------
symmetric/Hermitian simple driver SPTSV CPTSV DPTSV ZPTSV
positive definite expert driver SPTSVX CPTSVX DPTSVX ZPTSVX
tridiagonal
--------------------------------------------------------------------------
symmetric/Hermitian simple driver SSYSV CHESV DSYSV ZHESV
indefinite expert driver SSYSVX CHESVX DSYSVX ZHESVX
--------------------------------------------------------------------------
complex symmetric simple driver CSYSV ZSYSV
expert driver CSYSVX ZSYSVX
--------------------------------------------------------------------------
symmetric/Hermitian simple driver SSPSV CHPSV DSPSV ZHPSV
indefinite (packed expert driver SSPSVX CHPSVX DSPSVX ZHPSVX
storage)
--------------------------------------------------------------------------
complex symmetric simple driver CSPSV ZSPSV
(packed storage) expert driver CSPSVX ZSPSVX
--------------------------------------------------------------------------
Table 2.2: Driver routines for linear equations
Tue Nov 29 14:03:33 EST 1994
Linear Least Squares (LLS) Problems





Next:
Generalized Linear Least
Up:
Driver Routines
Previous:
Linear Equations
The linear least squares problem
is:

where A is an m-by-n matrix, b is a given m element vector
and x is the n element solution vector.
In the most usual case m > = n and rank(A) = n, and in this case the
solution to problem (
2.1) is unique,
and the problem is also
referred to as finding a least squares solution to an
overdetermined
system of linear equations.
When m < n and rank(A) = m, there are an infinite number
of solutions x
which exactly satisfy b - Ax = 0. In this case it is often useful to find
the unique solution x which minimizes  ,
and the problem
is referred to as finding a minimum norm solution
to an
underdetermined
system of linear equations.
,
and the problem
is referred to as finding a minimum norm solution
to an
underdetermined
system of linear equations.
The driver routine xGELS
solves problem (
2.1) on the assumption that
rank(A) = min(m , n) -- in other words, A has full rank -
finding a least squares solution of an overdetermined
system
when m > n, and a minimum norm solution of an underdetermined
system
when m < n.
xGELS
uses a QR or LQ factorization of A, and also allows A to be
replaced by  in the statement of the problem (or by
in the statement of the problem (or by  if A is
complex).
if A is
complex).
In the general case when we may have
rank(A) < min(m , n) -- in other words,
A may be rank-deficient -
we seek the minimum norm least squares solution
x
which minimizes both  and
and  .
.
The driver routines xGELSX
and xGELSS
solve this general formulation of problem
2.1,
allowing for the possibility that A is rank-deficient;
xGELSX
uses a complete orthogonal factorization of A,
while xGELSS
uses
the singular value decomposition of A.
The LLS
driver routines are listed in Table
2.3.
All three routines allow several right hand side vectors b and corresponding
solutions x to be handled in a single call, storing these vectors as columns
of matrices B and X, respectively.
Note however that problem
2.1 is solved for
each right hand side vector independently; this is not the same as
finding a matrix X which minimizes  .
.
-------------------------------------------------------------------
Single precision Double precision
Operation real complex real complex
-------------------------------------------------------------------
solve LLS using QR or SGELS CGELS DGELS ZGELS
LQ factorization
solve LLS using complete SGELSX CGELSX DGELSX ZGELSX
orthogonal factorization
solve LLS using SVD SGELSS CGELSS DGELSS ZGELSS
-------------------------------------------------------------------
Table 2.3: Driver routines for linear least squares problems





Next:
Generalized Linear Least
Up:
Driver Routines
Previous:
Linear Equations
Tue Nov 29 14:03:33 EST 1994
Preface to the Second Edition





Next:
Preface to the
Up:
List of Tables
Previous:
List of Tables
Since its initial public release in February 1992, LAPACK has expanded
in both depth and breadth. LAPACK is now available in both Fortran and C.
The publication of this second edition of the
Users' Guide coincides with the release of version 2.0
of the LAPACK software.
This release of LAPACK introduces
new routines and extends the functionality of
existing routines. Prominent among the new routines are
driver and computational routines for
the generalized nonsymmetric eigenproblem,
generalized linear least squares problems,
the generalized singular value decomposition,
a generalized banded symmetric-definite eigenproblem,
and divide-and-conquer methods for symmetric eigenproblems.
Additional computational routines include
the generalized QR and RQ factorizations and
reduction of a band matrix to bidiagonal form.
Added functionality has been incorporated into the expert driver
routines that involve equilibration (xGESVX, xGBSVX, xPOSVX, xPPSVX,
and xPBSVX). The option FACT = 'F' now permits the user to input a
prefactored, pre-equilibrated matrix. The expert drivers xGESVX and xGBSVX
now return the reciprocal of the pivot growth from Gaussian
elimination. xBDSQR has been modified to compute singular values of
bidiagonal matrices much more quickly than before, provided singular
vectors are not also wanted.
The least squares driver
routines xGELS, xGELSS, and xGELSX now make available the residual
root-sum-squares for each right hand side.
All LAPACK routines reflect the current version number with the
date on the routine indicating when it was last modified.
For more information on revisions to the LAPACK software or this Users'
Guide please refer to the LAPACK release_notes file on netlib.
Instructions for obtaining this file can be found in
Chapter
1.
On-line manpages (troff files) for LAPACK routines, as well as for most of
the BLAS routines, are available on netlib. Refer to
Section
1.6 for further details.
We hope that future releases of LAPACK will include routines for reordering
eigenvalues in the generalized Schur factorization;
solving the generalized Sylvester
equation; computing condition numbers for the generalized eigenproblem
(for eigenvalues, eigenvectors, clusters of eigenvalues, and deflating
subspaces);
fast algorithms for the singular value decomposition based on
divide and conquer;
high accuracy methods for symmetric eigenproblems and the SVD based
on Jacobi's algorithm;
updating and/or downdating for linear least squares problems;
computing singular values by bidiagonal
bisection; and computing singular vectors by bidiagonal inverse iteration.
The following additions/modifications have been made to this second edition
of the Users' Guide:
Chapter
1 (Essentials)
now includes information on accessing LAPACK via the World
Wide Web.
Chapter
2 (Contents of LAPACK) has been expanded to discuss
new routines.
Chapter
3 (Performance of LAPACK) has been updated
with performance results from version 2.0 of LAPACK. In addition,
a new section entitled ``LAPACK Benchmark'' has been introduced to
present timings for several driver routines.
Chapter
4 (Accuracy and Stability) has been simplified and
rewritten.
Much of the theory and other details have been separated into
``Further Details'' sections. Example Fortran code segments are
included to demonstrate the calculation of error bounds using LAPACK.
Appendices
A,
B, and
D have
been expanded to cover the new routines.
Appendix
E (LAPACK Working Notes) lists a number of new
Working Notes, written during the LAPACK 2 and ScaLAPACK
projects (see below) and published by the University of Tennessee.
The Bibliography has been updated to give
the most recent published references.
The Specifications of Routines have been extended and updated to cover
the new routines and revisions to existing routines.
The Bibliography and Index have been moved to the end of the book.
The Index has been expanded into two indexes: Index by Keyword and
Index by Routine Name. Occurrences of LAPACK, LINPACK, and EISPACK
routine names have been cited in the latter index.
The original LAPACK project was funded by the NSF. Since its completion,
two follow-up projects, LAPACK 2 and ScaLAPACK, have been funded in the
U.S. by the NSF and ARPA in 1990-1994 and 1991-1995, respectively.
In addition to making possible
the additions and extensions in this release, these grants have
supported the following closely related activities.
A major effort is underway
to implement LAPACK-type algorithms for distributed memory
machines.
As a result of these efforts,
several new software items are now available on netlib. The new
items that have been introduced are distributed memory versions of the
core routines from LAPACK; a fully parallel package to solve a symmetric
positive definite sparse linear system on a message passing
multiprocessor using Cholesky factorization
; a package based on
Arnoldi's method for solving large-scale nonsymmetric, symmetric, and
generalized algebraic eigenvalue problems
;
and templates for sparse
iterative methods for solving Ax = b.
For more information on the
availability of each of these packages, consult the scalapack
and linalg indexes on netlib via netlib@ornl.gov.
We have also explored the advantages of IEEE floating point arithmetic
[4]
in implementing linear algebra routines. The accurate rounding properties
and ``friendly'' exception handling capabilities of IEEE arithmetic
permit us to write faster, more robust versions of several algorithms in
LAPACK. Since all machines do not yet implement IEEE arithmetic, these
algorithms are not currently part of the library
[23],
although we expect them to be in the future. For more information,
please refer to Section
1.11.
LAPACK has been translated from Fortran into C and, in addition,
a subset of the LAPACK routines has been implemented in C++
.
For more information on obtaining the C or C++ versions of LAPACK, consult
Section
1.11 or the
clapack or c++ indexes on netlib via netlib@ornl.gov.
We deeply appreciate the careful scrutiny of those individuals who
reported mistakes, typographical errors, or shortcomings in the first
edition.
We acknowledge with gratitude the support which we have received from the
following organizations and the help of individual members of their staff:
Cray Research Inc.;
NAG Ltd.
We would additionally like to thank the following people, who were not
acknowledged in the first edition, for their contributions:
Françoise Chatelin,
Inderjit Dhillon,
Stan Eisenstat,
Vince Fernando,
Ming Gu,
Rencang Li,
Xiaoye Li,
George Ostrouchov,
Antoine Petitet,
Chris Puscasiu,
Huan Ren,
Jeff Rutter,
Ken Stanley,
Steve Timson,
and Clint Whaley.
* The royalties from the sales of this book are being placed in a
fund to help students attend SIAM meetings and other SIAM related
activities. This fund is administered by SIAM and qualified
individuals are encouraged to write directly to SIAM for guidelines.





Next:
Preface to the
Up:
List of Tables
Previous:
List of Tables
Tue Nov 29 14:03:33 EST 1994
Generalized Linear Least Squares (LSE and GLM) Problems





Next:
Standard Eigenvalue and
Up:
Driver Routines
Previous:
Linear Least Squares
Driver routines are provided for two types of generalized linear least squares
problems.
The first is

where A is an m-by-m matrix and B is a p-by-n matrix,
c is a given m-vector, and d is a given p-vector,
with p < = n < = m + p.
This is
called a linear equality-constrained least squares problem (LSE).
The routine xGGLSE
solves this problem using the generalized RQ
(GRQ) factorization,
on the
assumptions that B has full row rank p and
the matrix  has full column rank n.
Under these assumptions, the problem LSE
has a unique solution.
has full column rank n.
Under these assumptions, the problem LSE
has a unique solution.
The second generalized linear least squares problem is

where A is an n-by-m matrix, B is an n-by-p matrix,
and d is a given n-vector,
with m < = n < = m + p.
This is sometimes called a general (Gauss-Markov) linear model problem (GLM).
When B = I, the problem reduces to an ordinary linear least squares problem.
When B is square and nonsingular, the GLM problem is equivalent to the
weighted linear least squares problem:

The routine xGGGLM
solves this problem using the generalized QR (GQR)
factorization,
on the
assumptions that A has full column rank m, and the
matrix (A , B) has full row rank n. Under these assumptions, the
problem is always consistent, and there are unique solutions x and y.
The driver routines for generalized linear least squares problems are listed
in Table
2.4.
------------------------------------------------------------------
Single precision Double precision
Operation real complex real complex
------------------------------------------------------------------
solve LSE problem using GQR SGGLSE CGGLSE DGGLSE ZGGLSE
solve GLM problem using GQR SGGGLM CGGGLM DGGGLM ZGGGLM
------------------------------------------------------------------
Table 2.4: Driver routines for generalized linear least squares problems
Tue Nov 29 14:03:33 EST 1994
Standard Eigenvalue and Singular Value Problems





Next:
Symmetric Eigenproblems (SEP)
Up:
Driver Routines
Previous:
Generalized Linear Least
Tue Nov 29 14:03:33 EST 1994
Symmetric Eigenproblems (SEP)





Next:
Nonsymmetric Eigenproblems (NEP)
Up:
Standard Eigenvalue and
Previous:
Standard Eigenvalue and
The symmetric eigenvalue problem is to find the eigenvalues
,
 , and corresponding eigenvectors
,
, and corresponding eigenvectors
,  , such that
, such that

For the Hermitian eigenvalue problem we have

For both problems the eigenvalues  are real.
are real.
When all eigenvalues and eigenvectors have been computed, we write:

where  is a diagonal matrix whose diagonal elements are the
eigenvalues
, and Z is an orthogonal (or unitary) matrix whose columns
are the eigenvectors. This is the classical spectral factorization
of A.
is a diagonal matrix whose diagonal elements are the
eigenvalues
, and Z is an orthogonal (or unitary) matrix whose columns
are the eigenvectors. This is the classical spectral factorization
of A.
Three types of driver routines
are provided for symmetric or Hermitian
eigenproblems:
- a simple driver (name ending -EV)
,
which computes all the eigenvalues and
(optionally) the eigenvectors of a symmetric or Hermitian matrix A;
- a divide and conquer driver
(name ending -EVD)
, which computes
all the eigenvalues and (optionally) the
eigenvectors of a symmetric or Hermitian matrix A using an algorithm
based on divide and conquer
; the -EVD routines
can be much faster than their -EV counterparts, but use more workspace;
- an expert driver (name ending -EVX)
,
which can compute either all or a selected subset of the eigenvalues,
and (optionally) the corresponding eigenvectors.
Different driver routines are provided to take advantage of special
structure or storage of the matrix A, as shown in
Table
2.5.
In the future LAPACK will include routines based on the Jacobi algorithm
[76]
[69]
[24],
which are slower than the above routines but can be significantly more accurate.
Tue Nov 29 14:03:33 EST 1994
Nonsymmetric Eigenproblems (NEP)





Next:
Singular Value Decomposition
Up:
Standard Eigenvalue and
Previous:
Symmetric Eigenproblems (SEP)
The nonsymmetric eigenvalue problem is to find the eigenvalues
,
 , and corresponding eigenvectors
,
, and corresponding eigenvectors
,  , such that
, such that

A real matrix A may have complex eigenvalues, occurring as complex conjugate
pairs. More precisely, the vector v is called a right
eigenvector
of A, and a vector  satisfying
satisfying

is called a left eigenvector
of A.
This problem can be solved
via the Schur factorization
of A,
defined in the real case as

where Z is an orthogonal matrix and T is an upper quasi-triangular matrix
with 1-by-1 and 2-by-2 diagonal blocks, the 2-by-2 blocks
corresponding to complex conjugate pairs of eigenvalues of A. In the complex
case the Schur factorization is

where Z is unitary and T is a complex upper triangular matrix.
The columns of Z are called the Schur vectors
.
For each k (1 < = k < = n)
, the first k columns of Z form an orthonormal
basis for the invariant subspace corresponding to the
first k eigenvalues on the diagonal of T. Because this
basis is orthonormal, it is preferable in many
applications to compute Schur vectors rather than
eigenvectors. It is possible to order the Schur
factorization so that any desired set of k eigenvalues
occupy the k leading positions on the diagonal of T.
Two pairs of drivers
are provided, one pair focusing on the Schur
factorization, and the other pair on the eigenvalues and eigenvectors
as shown in Table
2.5:
- xGEES
: a simple driver that computes all or part of the Schur
factorization of A, with optional ordering of the eigenvalues;
- xGEESX
: an expert driver that can additionally compute condition
numbers for the average of a selected subset of the eigenvalues, and for
the corresponding right invariant subspace;
- xGEEV
: a simple driver that computes all the eigenvalues of A,
and (optionally) the right or left eigenvectors (or both);
- xGEEVX
: an expert driver that can additionally balance the
matrix to improve the conditioning of the eigenvalues and eigenvectors,
and compute condition numbers for the eigenvalues or right eigenvectors
(or both).





Next:
Singular Value Decomposition
Up:
Standard Eigenvalue and
Previous:
Symmetric Eigenproblems (SEP)
Tue Nov 29 14:03:33 EST 1994
Singular Value Decomposition (SVD)





Next:
Generalized Eigenvalue and
Up:
Standard Eigenvalue and
Previous:
Nonsymmetric Eigenproblems (NEP)
The singular value decomposition of an m-by-n matrix A is given by

where U and V are orthogonal (unitary)
and  is an m-by-n diagonal matrix with real
diagonal elements,
is an m-by-n diagonal matrix with real
diagonal elements,  , such that
, such that

The  are the singular values of A and the
first min(m , n) columns of U and V
are the left and right singular vectors of A.
are the singular values of A and the
first min(m , n) columns of U and V
are the left and right singular vectors of A.
The singular values and singular vectors satisfy:

where  and
and  are the i-th columns of U and V respectively.
are the i-th columns of U and V respectively.
A single driver
routine xGESVD
computes
all or part of the
singular value decomposition of a general nonsymmetric matrix
(see Table
2.5).
A future version of LAPACK will
include a driver based on divide and conquer, as in
section
2.2.4.1.
--------------------------------------------------------------------------
Type of Single precision Double precision
problem Function and storage scheme real complex real complex
--------------------------------------------------------------------------
SEP simple driver SSYEV CHEEV DSYEV ZHEEV
expert driver SSYEVX CHEEVX DSYEVX ZHEEVX
--------------------------------------------------------------------------
simple driver (packed storage) SSPEV CHPEV DSPEV ZHPEV
expert driver (packed storage) SSPEVX CHPEVX DSPEVX ZHPEVX
--------------------------------------------------------------------------
simple driver (band matrix) SSBEV CHBEV DSBEV ZHBEV
expert driver (band matrix) SSBEVX CHBEVX DSBEVX ZHBEVX
--------------------------------------------------------------------------
simple driver (tridiagonal SSTEV DSTEV
matrix)
expert driver (tridiagonal SSTEVX DSTEVX
matrix)
--------------------------------------------------------------------------
NEP simple driver for SGEES CGEES DGEES ZGEES
Schur factorization
expert driver for SGEESX CGEESX DGEESX ZGEESX
Schur factorization
simple driver for SGEEV CGEEV DGEEV ZGEEV
eigenvalues/vectors
expert driver for SGEEVX CGEEVX DGEEVX ZGEEVX
eigenvalues/vectors
--------------------------------------------------------------------------
SVD singular values/vectors SGESVD CGESVD DGESVD ZGESVD
--------------------------------------------------------------------------
Table 2.5: Driver routines for standard eigenvalue and singular value problems
Tue Nov 29 14:03:33 EST 1994
Generalized Eigenvalue and Singular Value
Problems





Next:
Generalized Symmetric Definite
Up:
Driver Routines
Previous:
Singular Value Decomposition
Tue Nov 29 14:03:33 EST 1994
Generalized Symmetric Definite Eigenproblems (GSEP)





Next:
Generalized Nonsymmetric Eigenproblems
Up:
Generalized Eigenvalue and
Previous:
Generalized Eigenvalue and
Simple drivers are provided to compute all the eigenvalues and
(optionally) the eigenvectors of the following types of problems:
-

-

-

where A and B are symmetric or Hermitian and B is positive definite.
For all these problems the eigenvalues
 are real. The matrices Z
of computed eigenvectors
satisfy
are real. The matrices Z
of computed eigenvectors
satisfy
 (problem types 1 and 3) or
(problem types 1 and 3) or  (problem type 2), where
(problem type 2), where  is a diagonal matrix with the eigenvalues
on the diagonal. Z also satisfies
is a diagonal matrix with the eigenvalues
on the diagonal. Z also satisfies
 (problem types 1 and 2) or
(problem types 1 and 2) or  (problem type 3).
(problem type 3).
The routines are listed in Table
2.6.
Tue Nov 29 14:03:33 EST 1994
Generalized Nonsymmetric Eigenproblems (GNEP)





Next:
Generalized Singular Value
Up:
Generalized Eigenvalue and
Previous:
Generalized Symmetric Definite
Given two square matrices A and B,
the generalized nonsymmetric eigenvalue problem is to find
the eigenvalues  and corresponding
eigenvectors
and corresponding
eigenvectors
 such that
such that

or
find the eigenvalues  and corresponding eigenvectors
and corresponding eigenvectors
 such that
such that

Note that these problems are equivalent with  and
and  if neither
if neither  nor
nor  is zero.
In order to deal with the case that
is zero.
In order to deal with the case that  or
or  is zero, or nearly so,
the LAPACK routines return two values,
is zero, or nearly so,
the LAPACK routines return two values,  and
and  , for each
eigenvalue, such that
, for each
eigenvalue, such that  and
and  .
.
More precisely,  and
and  are called right eigenvectors. Vectors
are called right eigenvectors. Vectors
 or
or  satisfying
satisfying

are called left eigenvectors.
If the determinant of  is zero for all values of
is zero for all values of  ,
the eigenvalue problem is called singular, and is signaled by some
,
the eigenvalue problem is called singular, and is signaled by some
 (in the presence of roundoff,
(in the presence of roundoff,  and
and  may
be very small). In this case the eigenvalue problem is very ill-conditioned,
and in fact some of the other nonzero values of
may
be very small). In this case the eigenvalue problem is very ill-conditioned,
and in fact some of the other nonzero values of  and
and  may be
indeterminate
[21]
[80]
[71].
may be
indeterminate
[21]
[80]
[71].
The generalized nonsymmetric eigenvalue problem can be solved via the
generalized Schur factorization
of the pair A,B, defined in the
real case as

where Q and Z are orthogonal matrices, P is upper triangular,
and S is an upper quasi-triangular matrix
with 1-by-1 and 2-by-2 diagonal blocks, the 2-by-2 blocks
corresponding to complex conjugate pairs of eigenvalues of A,B.
In the complex
case the Schur factorization is

where Q and Z are unitary and S and P are both upper triangular.
The columns of Q and Z are called generalized Schur vectors
and span pairs of deflating subspaces of A and B
[72].
Deflating subspaces are a generalization of invariant subspaces:
For each k (1 < = k < = n),
the first k columns of Z span a right deflating subspace
mapped by both A and B into a left deflating subspace spanned by
the first k columns of Q.
Two simple drivers are provided for the nonsymmetric problem
 :
:
- xGEGS
: computes
all or part of the generalized Schur factorization
of the pencil
 ;
;
- xGEGV
: computes
all the generalized eigenvalues, and (optionally) the
right or left eigenvectors (or both);
as shown in Table
2.6. In later versions of LAPACK we plan
to provide expert drivers analogous to xGEESX and xGEEVX.





Next:
Generalized Singular Value
Up:
Generalized Eigenvalue and
Previous:
Generalized Symmetric Definite
Tue Nov 29 14:03:33 EST 1994
Generalized Singular Value Decomposition (GSVD)





Next:
Computational Routines
Up:
Generalized Eigenvalue and
Previous:
Generalized Nonsymmetric Eigenproblems
The generalized (or quotient) singular value decomposition
of an m-by-n matrix A and a
p-by-n matrix B is given by the pair of factorizations

The matrices in these factorizations have the following properties:
- U is m-by-m, V is p-by-p, Q is n-by-n, and
all three matrices are orthogonal. If A and
B are complex, these matrices are unitary instead of
orthogonal, and
 should be
replaced by
should be
replaced by  in the pair of factorizations.
in the pair of factorizations.
- R is r-by-r, upper triangular and nonsingular.
[0 , R] is r-by-n (in other words, the 0 is an h-by-n - r
zero matrix).
The integer r is the rank of
 , and satisfies r < = n.
, and satisfies r < = n.
-
 is m-by-r,
is m-by-r,
 is p-by-r, both are real, nonnegative and diagonal, and
is p-by-r, both are real, nonnegative and diagonal, and
 .
Write
.
Write
 and
and
 ,
where
,
where  and
and  lie in the interval from 0 to 1.
The ratios
lie in the interval from 0 to 1.
The ratios
 are called the generalized singular values of the pair A,B,
are called the generalized singular values of the pair A,B,  .
If
.
If  , then the generalized singular value
, then the generalized singular value
 is infinite.
is infinite.
 and
and  have the following detailed
structures, depending on whether m - r > = 0 or
m - r < 0. In the first case, m - r > = 0, then
have the following detailed
structures, depending on whether m - r > = 0 or
m - r < 0. In the first case, m - r > = 0, then

Here l is the rank of B, m = r - 1, C and S are diagonal
matrices satisfying  , and S is nonsingular.
We may also identify
, and S is nonsingular.
We may also identify
 ,
,
 for
for  ,
,
 , and
, and
 for
for  .
Thus, the first k generalized singular values
.
Thus, the first k generalized singular values
 are infinite, and the remaining l generalized singular values
are finite.
are infinite, and the remaining l generalized singular values
are finite.
In the second case, when m - r < 0,

and

Again, l is the rank of B, k = r - 1, C and S are diagonal
matrices satisfying  , S is nonsingular,
and we may identify
, S is nonsingular,
and we may identify
 ,
,
 for
for  ,
,
 ,
,
 ,
,
 for
for  , and
, and
 .
Thus, the first
.
Thus, the first  generalized singular values
generalized singular values
 are infinite, and the remaining
are infinite, and the remaining  generalized singular values
are finite.
generalized singular values
are finite.
Here are some important special cases of the generalized singular value
decomposition.
First, if B is square and nonsingular, then r = n and the
generalized singular value decomposition of A and B is equivalent
to the singular value decomposition of  , where the singular
values of
, where the singular
values of  are equal to the generalized singular values of the
pair A,B:
are equal to the generalized singular values of the
pair A,B:

Second, if
the columns of  are orthonormal, then r = n, R = I and the
generalized
singular value decomposition of A and B is equivalent to the CS
(Cosine-Sine) decomposition of
are orthonormal, then r = n, R = I and the
generalized
singular value decomposition of A and B is equivalent to the CS
(Cosine-Sine) decomposition of  [45]:
[45]:

Third, the generalized eigenvalues and eigenvectors of  can be expressed in terms of the generalized singular value decomposition:
Let
can be expressed in terms of the generalized singular value decomposition:
Let

Then

Therefore, the columns of X are the eigenvectors of
 , and the ``nontrivial'' eigenvalues are the
squares of the generalized singular values (see also section
2.2.5.1).
``Trivial'' eigenvalues
are those corresponding to the leading n - r columns of X,
which span the common null space of
, and the ``nontrivial'' eigenvalues are the
squares of the generalized singular values (see also section
2.2.5.1).
``Trivial'' eigenvalues
are those corresponding to the leading n - r columns of X,
which span the common null space of  and
and  .
The ``trivial eigenvalues'' are not well defined
.
The ``trivial eigenvalues'' are not well defined
 .
.
A single driver routine xGGSVD
computes the generalized
singular value decomposition
of A and B (see Table
2.6).
The method is based on the method described in
[12]
[10]
[62].
----------------------------------------------------------------
Type of Function and Single precision Double precision
problem storage scheme real complex real complex
----------------------------------------------------------------
GSEP simple driver SSYGV CHEGV DSYGV ZHEGV
simple driver SSPGV CHPGV DSPGV ZHPGV
(packed storage)
simple driver SSBGV CHBGV DSBGV ZHBGV
(band matrices)
----------------------------------------------------------------
GNEP simple driver for SGEGS CGEGS DGEGS ZGEGS
Schur factorization
simple driver for SGEGV CGEGV DGEGV ZGEGV
eigenvalues/vectors
----------------------------------------------------------------
GSVD singular values/ SGGSVD CGGSVD DGGSVD ZGGSVD
vectors
-----------------------------------------------------------------
Table 2.6: Driver routines for generalized eigenvalue and singular value problems





Next:
Computational Routines
Up:
Generalized Eigenvalue and
Previous:
Generalized Nonsymmetric Eigenproblems
Tue Nov 29 14:03:33 EST 1994
Computational Routines





Next:
Linear Equations
Up:
Contents of LAPACK
Previous:
Generalized Singular Value
Tue Nov 29 14:03:33 EST 1994
Preface to the First Edition





Next:
Guide
Up:
List of Tables
Previous:
Preface to the
The development of LAPACK was a natural step after specifications of
the Level 2 and 3 BLAS were drawn up in 1984-86 and 1987-88.
Research on block algorithms had been ongoing for several years,
but agreement on the BLAS made it possible to construct a new
software package to take the place of LINPACK and EISPACK,
which would achieve much greater efficiency on modern high-performance
computers.
This also seemed to be a good time to implement a number of
algorithmic advances that had been made since LINPACK and EISPACK
were written in the 1970's.
The proposal for LAPACK was submitted while the Level 3 BLAS were
still being developed and funding was obtained from the National
Science Foundation (NSF) beginning in 1987.
LAPACK is more than just a more efficient update of its popular predecessors.
It extends the functionality of LINPACK and EISPACK by including:
driver routines for linear systems;
equilibration, iterative
refinement and error
bounds for linear systems;
routines for computing and re-ordering the Schur
factorization;
and condition estimation routines for eigenvalue problems.
LAPACK improves on the accuracy of the standard algorithms in EISPACK
by including high accuracy algorithms for finding singular values and
eigenvalues of bidiagonal and tridiagonal matrices, respectively,
that arise in SVD and symmetric eigenvalue problems.
We have tried to be consistent with our documentation and
coding style throughout LAPACK in the hope that LAPACK will serve
as a model for other software development efforts.
In particular, we hope that LAPACK and this guide will
be of value in the classroom.
But above all, LAPACK has been designed to be used for serious
computation, especially
as a source of building blocks for larger applications.
The LAPACK project has been a research project on achieving good
performance in a portable way over a large class of modern computers.
This goal has been achieved, subject to the following qualifications.
For optimal performance, it is necessary, first, that
the BLAS are implemented efficiently on the
target machine, and second, that a small number of tuning parameters
(such as the block size) have been set to suitable values
(reasonable default values are provided).
Most of the LAPACK code is written in standard Fortran 77,
but the double precision complex data type is not part of the standard,
so we have had to make some assumptions about the names of intrinsic
functions that do not hold on all machines (see section
6.1).
Finally, our rigorous testing suite included test problems scaled
at the extremes of the arithmetic range,
which can vary greatly from machine to machine.
On some machines, we have had to restrict the range more than on others.
Since most of the performance improvements in LAPACK come from
restructuring the algorithms to use the Level 2 and 3 BLAS,
we benefited greatly by having access from the early stages of the
project to a complete set of BLAS developed for the CRAY machines
by Cray Research. Later, the BLAS library developed by IBM for the
IBM RISC/6000 was very helpful in proving the worth of block algorithms
and LAPACK on ``super-scalar'' workstations. Many of our test sites, both
computer vendors and research institutions, also worked on optimizing
the BLAS and thus helped to get good performance from LAPACK.
We are very pleased at the extent to which the user community has
embraced the BLAS, not only for performance reasons, but also because
we feel developing software around a core set of common routines
like the BLAS is good software engineering practice.
A number of technical reports were written during the development of
LAPACK and published as LAPACK Working Notes, initially by Argonne
National Laboratory and later by the University of Tennessee.
Many of these reports later appeared as journal articles.
Appendix
E lists the LAPACK Working Notes,
and the Bibliography gives the
most recent published reference.
A follow-on project, LAPACK 2, has been funded in the U.S. by the NSF
and DARPA.
One of its aims will be to add a modest amount of additional
functionality to the current LAPACK package - for example,
routines for the generalized SVD and additional routines for
generalized eigenproblems. These routines will be included in a future
release of LAPACK when they are available.
LAPACK 2 will also produce routines which implement LAPACK-type
algorithms for distributed memory machines, routines which take special
advantage of IEEE arithmetic, and versions of parts of LAPACK in
C and Fortran 90.
The precise form of these other software packages which will
result from LAPACK 2 has not yet been decided.
As the successor to LINPACK and EISPACK, LAPACK has drawn
heavily on both the software and documentation from those collections.
The test and timing software for the Level 2 and 3 BLAS was
used as a model for the LAPACK test and timing software, and in
fact the LAPACK timing software includes the BLAS timing software
as a subset.
Formatting of the software and conversion from single to double
precision was done using Toolpack/1
[66], which was
indispensable to the project.
We owe a great debt to our colleagues
who have helped create the infrastructure of scientific computing on
which LAPACK has been built.
The development of LAPACK was primarily supported by NSF grant
ASC-8715728.
Zhaojun Bai
had partial support from DARPA grant F49620-87-C0065;
Christian Bischof was supported by the Applied
Mathematical Sciences subprogram of the Office of Energy Research,
U.S. Department of Energy, under contract W-31-109-Eng-38; James
Demmel had partial support from NSF grant DCR-8552474;
and
Jack Dongarra had partial support from the
Applied Mathematical Sciences subprogram
of the Office of Energy Research, U.S.
Department of Energy, under Contract
DE-AC05-84OR21400.
The cover was designed by Alan Edelman at UC Berkeley who discovered the matrix
by performing Gaussian elimination on a certain 20-by-20 Hadamard matrix.
We acknowledge with gratitude the support which we have received from the
following organizations, and the help of individual members of their staff:
Cornell Theory Center;
Cray Research Inc.;
IBM ECSEC Rome;
IBM Scientific Center, Bergen;
NAG Ltd.
We also thank many, many people who have contributed code,
criticism, ideas and encouragement.
We wish especially to acknowledge the contributions of:
Mario Arioli,
Mir Assadullah,
Jesse Barlow,
Mel Ciment,
Percy Deift,
Augustin Dubrulle,
Iain Duff,
Alan Edelman,
Victor Eijkhout,
Sam Figueroa,
Pat Gaffney,
Nick Higham,
Liz Jessup,
Bo Kågström,
Velvel Kahan,
Linda Kaufman,
L.-C. Li,
Bob Manchek,
Peter Mayes,
Cleve Moler,
Beresford Parlett,
Mick Pont,
Giuseppe Radicati,
Tom Rowan,
Pete Stewart,
Peter Tang,
Carlos Tomei,
Charlie Van Loan,
Kresimir Veselic,
Phuong Vu,
and Reed Wade.
Finally we thank all the test sites who received three preliminary
distributions of LAPACK software and who ran an extensive series of
test programs and timing programs for us; their efforts have influenced
the final version of the package in numerous ways.
* The royalties from the sales of this book are being placed in a
fund to help students attend SIAM meetings and other SIAM related
activities. This fund is administered by SIAM and qualified
individuals are encouraged to write directly to SIAM for guidelines.





Next:
Guide
Up:
List of Tables
Previous:
Preface to the
Tue Nov 29 14:03:33 EST 1994
Linear Equations





Next:
Orthogonal Factorizations and
Up:
Computational Routines
Previous:
Computational Routines
We use the standard notation for a system of simultaneous
linear
equations
:
Ax = b
where A is the coefficient matrix,
b is the right hand side,
and x is the solution.
In (
2.4) A is assumed to be a square matrix of order n,
but some of the individual routines allow A to be rectangular.
If there are several right hand sides,
we write
AX = B
where the columns of B are the individual right hand sides,
and the columns of
X are the corresponding solutions.
The basic task is to compute X, given A and B.
If A is upper or lower triangular, (
2.4) can be solved by a
straightforward
process of backward or forward substitution.
Otherwise, the solution is obtained after first factorizing A as a
product of
triangular matrices (and possibly also a diagonal matrix or permutation
matrix).
The form of the factorization depends on the properties of the matrix
A.
LAPACK provides routines for the following types of matrices, based on
the stated
factorizations:
- general matrices
(LU factorization with partial pivoting):
A = PLU
where P is a permutation matrix, L is lower triangular with unit
diagonal elements (lower trapezoidal if m > n), and U is upper
triangular (upper trapezoidal if m < n).
- general band matrices including tridiagonal matrices
(LU factorization with partial pivoting):
If A is m-by-m with kl subdiagonals and ku superdiagonals,
the factorization is
A = LU
where L is a product of permutation and unit lower triangular
matrices with kl subdiagonals, and U is upper triangular with
kl + ku superdiagonals.
- symmetric and Hermitian positive definite matrices including
band matrices (Cholesky factorization):


where U is an upper triangular matrix and L is lower triangular.
- symmetric and Hermitian positive definite tridiagonal matrices (
 factorization):
factorization):


where U is a unit upper bidiagonal matrix, L is unit lower
bidiagonal, and D is diagonal.
- symmetric and Hermitian indefinite matrices (symmetric indefinite
factorization)
:


where U (or L) is a product of permutation and unit upper (lower)
triangular matrices, and D is symmetric and block diagonal with diagonal
blocks of order 1 or 2.
The factorization for a general tridiagonal matrix is like that for
a general band matrix with kl = 1 and ku = 1. The factorization
for a symmetric positive definite band matrix with k superdiagonals
(or
subdiagonals) has the same form as for a symmetric positive definite
matrix, but the factor U (or L) is a band matrix with k
superdiagonals (subdiagonals). Band matrices use a compact band
storage scheme described in section
5.3.3.
LAPACK routines are also provided for symmetric matrices (whether
positive definite or indefinite) using packed storage,
as described in section
5.3.2.
While the primary use of a matrix factorization is to solve a system
of equations, other related tasks are provided as well.
Wherever possible, LAPACK provides routines to perform each of these
tasks
for each type of matrix and storage scheme (see
Tables
2.7 and
2.8).
The following list relates the tasks
to the last 3 characters of the name of the corresponding
computational routine:
- xyyTRF:
- factorize (obviously not needed for triangular matrices);
- xyyTRS:
- use the factorization (or the matrix A itself if it is
triangular) to
solve (
2.5) by forward or backward substitution;
- xyyCON:
- estimate the reciprocal of the condition number
 ;
Higham's modification
[52] of Hager's method
[48]
is used to estimate
;
Higham's modification
[52] of Hager's method
[48]
is used to estimate  ,
except for symmetric positive definite tridiagonal matrices for which it
is computed directly with comparable efficiency
[50];
,
except for symmetric positive definite tridiagonal matrices for which it
is computed directly with comparable efficiency
[50];
- xyyRFS:
- compute bounds on the error in the computed solution (returned
by the xyyTRS routine), and
refine the solution to reduce the backward error (see below);
- xyyTRI:
- use the factorization (or the matrix A itself if it is
triangular)
to compute
 (not provided for band matrices, because the inverse
does not in general preserve bandedness);
(not provided for band matrices, because the inverse
does not in general preserve bandedness);
- xyyEQU:
- compute scaling factors to equilibrate
A
(not provided for tridiagonal, symmetric
indefinite, or triangular matrices). These routines do not actually scale
the matrices: auxiliary routines xLAQyy may be used for that purpose -
see the code of the driver routines xyySVX for sample usage
.
Note that some of the above routines depend on the output of others:
- xyyTRF:
- may work on an equilibrated matrix produced by
xyyEQU and xLAQyy, if yy is one of {GE, GB, PO, PP, PB};
- xyyTRS:
- requires the factorization returned by xyyTRF;
- xyyCON:
- requires the norm of the original matrix A, and the
factorization returned by xyyTRF;
- xyyRFS:
- requires the original matrices A and B, the factorization
returned by xyyTRF, and the solution X returned by xyyTRS;
- xyyTRI:
- requires the factorization returned by xyyTRF.
The RFS (``refine solution'') routines perform iterative
refinement
and compute backward and forward error
bounds for the solution.
Iterative refinement is done in the same precision as the input data.
In particular, the residual is not computed with extra precision,
as has been traditionally done.
The benefit of this procedure is discussed in Section
4.4.
--------------------------------------------------------------------------------
Type of matrix Operation Single precision Double precision
and storage scheme real complex real complex
--------------------------------------------------------------------------------
general factorize SGETRF CGETRF DGETRF ZGETRF
solve using factorization SGETRS CGETRS DGETRS ZGETRS
estimate condition number SGECON CGECON DGECON ZGECON
error bounds for solution SGERFS CGERFS DGERFS ZGERFS
invert using factorization SGETRI CGETRI DGETRI ZGETRI
equilibrate SGEEQU CGEEQU DGEEQU ZGEEQU
--------------------------------------------------------------------------------
general factorize SGBTRF CGBTRF DGBTRF ZGBTRF
band solve using factorization SGBTRS CGBTRS DGBTRS ZGBTRS
estimate condition number SGBCON CGBCON DGBCON ZGBCON
error bounds for solution SGBRFS CGBRFS DGBRFS ZGBRFS
equilibrate SGBEQU CGBEQU DGBEQU ZGBEQU
--------------------------------------------------------------------------------
general factorize SGTTRF CGTTRF DGTTRF ZGTTRF
tridiagonal solve using factorization SGTTRS CGTTRS DGTTRS ZGTTRS
estimate condition number SGTCON CGTCON DGTCON ZGTCON
error bounds for solution SGTRFS CGTRFS DGTRFS ZGTRFS
--------------------------------------------------------------------------------
symmetric/ factorize SPOTRF CPOTRF DPOTRF ZPOTRF
Hermitian solve using factorization SPOTRS CPOTRS DPOTRS ZPOTRS
positive definite estimate condition number SPOCON CPOCON DPOCON ZPOCON
error bounds for solution SPORFS CPORFS DPORFS ZPORFS
invert using factorization SPOTRI CPOTRI DPOTRI ZPOTRI
equilibrate SPOEQU CPOEQU DPOEQU ZPOEQU
--------------------------------------------------------------------------------
symmetric/ factorize SPPTRF CPPTRF DPPTRF ZPPTRF
Hermitian solve using factorization SPPTRS CPPTRS DPPTRS ZPPTRS
positive definite estimate condition number SPPCON CPPCON DPPCON ZPPCON
(packed storage) error bounds for solution SPPRFS CPPRFS DPPRFS ZPPRFS
invert using factorization SPPTRI CPPTRI DPPTRI ZPPTRI
equilibrate SPPEQU CPPEQU DPPEQU ZPPEQU
--------------------------------------------------------------------------------
symmetric/ factorize SPBTRF CPBTRF DPBTRF ZPBTRF
Hermitian solve using factorization SPBTRS CPBTRS DPBTRS ZPBTRS
positive definite estimate condition number SPBCON CPBCON DPBCON ZPBCON
band error bounds for solution SPBRFS CPBRFS DPBRFS ZPBRFS
equilibrate SPBEQU CPBEQU DPBEQU ZPBEQU
--------------------------------------------------------------------------------
symmetric/ factorize SPTTRF CPTTRF DPTTRF ZPTTRF
Hermitian solve using factorization SPTTRS CPTTRS DPTTRS ZPTTRS
positive definite estimate condition number SPTCON CPTCON DPTCON ZPTCON
tridiagonal error bounds for solution SPTRFS CPTRFS DPTRFS ZPTRFS
--------------------------------------------------------------------------------
Table 2.7: Computational routines for linear equations

Table 2.8: Computational routines for linear equations (continued)





Next:
Orthogonal Factorizations and
Up:
Computational Routines
Previous:
Computational Routines
Tue Nov 29 14:03:33 EST 1994
Orthogonal Factorizations and Linear Least Squares Problems





Next:
Factorization
Up:
Computational Routines
Previous:
Linear Equations
LAPACK provides a number of routines for factorizing a general
rectangular m-by-n matrix A,
as the product of an orthogonal matrix (unitary if complex)
and a triangular (or possibly trapezoidal) matrix.
A real matrix Q is orthogonal if  ;
a complex matrix Q is unitary if
;
a complex matrix Q is unitary if  .
Orthogonal or unitary matrices have the important property that they leave the
two-norm of a vector invariant:
.
Orthogonal or unitary matrices have the important property that they leave the
two-norm of a vector invariant:

As a result, they help to maintain numerical stability because they do not
amplify rounding errors.
Orthogonal factorizations
are used in
the solution of linear least squares problems
.
They may also be used to perform preliminary
steps in the solution of eigenvalue or
singular value problems.
Tue Nov 29 14:03:33 EST 1994
<var>QR</var> Factorization





Next:
Factorization
Up:
Orthogonal Factorizations and
Previous:
Orthogonal Factorizations and
The most
common, and best known, of the factorizations
is the QR factorization
given by

where R is an n-by-n upper triangular matrix and Q is an m-by-m
orthogonal (or unitary) matrix. If A is of full rank n, then R is
non-singular.
It is sometimes convenient to write the factorization as

which reduces to

where  consists of the first n columns of Q, and
consists of the first n columns of Q, and  the
remaining m - n columns.
the
remaining m - n columns.
If m < n, R is trapezoidal, and the factorization can be written

where  is upper triangular and
is upper triangular and  is rectangular.
is rectangular.
The routine xGEQRF
computes the QR factorization. The matrix Q is not
formed explicitly, but is represented as a product of elementary reflectors,
as described in section
5.4.
Users need not be aware of the details of this representation,
because associated routines are provided to work with Q:
xORGQR
(or xUNGQR
in the complex case) can generate all or part of R,
while xORMQR
(or xUNMQR
) can pre- or post-multiply
a given matrix by Q or  (
( if complex).
if complex).
The QR factorization can be used to solve the linear least squares
problem (
2.1)
when m > = n and
A is of full rank, since

c can be computed by xORMQR
(or xUNMQR
), and  consists of its first
n elements. Then
x is the solution of the upper triangular system
consists of its first
n elements. Then
x is the solution of the upper triangular system

which can be computed by xTRTRS
.
The residual vector r is given by

and may be computed using xORMQR
(or xUNMQR
).
The residual sum of squares  may be computed without forming r
explicitly, since
may be computed without forming r
explicitly, since

Tue Nov 29 14:03:33 EST 1994
LQ Factorization





Next:
Factorization with Column
Up:
Orthogonal Factorizations and
Previous:
Factorization
The LQ factorization
is given by

where L is m-by-m lower triangular, Q is n-by-n
orthogonal (or unitary),  consists of the first m rows of Q,
and
consists of the first m rows of Q,
and  the remaining n - m rows.
the remaining n - m rows.
This factorization is computed by the routine xGELQF, and again Q is
represented as a product of elementary reflectors; xORGLQ
(or xUNGLQ
in the complex case) can generate
all or part of Q, and xORMLQ
(or xUNMLQ
) can pre- or post-multiply a given
matrix
by Q or  (
( if Q is complex).
if Q is complex).
The LQ factorization of A is essentially the same as the QR factorization
of  (
( if A is complex), since
if A is complex), since

The LQ factorization may be used to find a minimum norm solution
of
an underdetermined
system of linear equations Ax = b where A is
m-by-n with m < n and has rank m. The solution is given by

and may be computed by calls to xTRTRS and xORMLQ.
Tue Nov 29 14:03:33 EST 1994
<var>QR</var> Factorization with Column Pivoting





Next:
Complete Orthogonal Factorization
Up:
Orthogonal Factorizations and
Previous:
Factorization
To solve a linear least squares problem (
2.1)
when A is not of full rank, or the rank of A is in doubt, we can
perform either a QR factorization with column pivoting
or a singular value
decomposition (see subsection
2.3.6).
The QR factorization with column pivoting is given by

where Q and R are as before and P is a permutation matrix, chosen
(in general) so that

and moreover, for each k,

In exact arithmetic, if rank(A) = k, then the whole of the submatrix
 in rows and columns k + 1 to n
would be zero. In numerical computation, the aim must be to
determine an index k, such that the leading submatrix
in rows and columns k + 1 to n
would be zero. In numerical computation, the aim must be to
determine an index k, such that the leading submatrix  in the first
k rows and columns is well-conditioned, and
in the first
k rows and columns is well-conditioned, and  is negligible:
is negligible:

Then k is the effective rank of A.
See Golub and Van Loan
[45]
for a further discussion of numerical rank determination.
The so-called basic solution to the linear least squares
problem (
2.1)
can be obtained from this factorization as

where  consists of just the first k elements of
consists of just the first k elements of  .
.
The routine xGEQPF
computes the QR factorization with column pivoting,
but does not attempt to determine the rank of A.
The matrix Q is represented in exactly the same way as after a call of
xGEQRF
, and so the routines xORGQR and xORMQR can be used to work with Q
(xUNGQR and xUNMQR if Q is complex).
Tue Nov 29 14:03:33 EST 1994
Complete Orthogonal Factorization





Next:
Other Factorizations
Up:
Orthogonal Factorizations and
Previous:
Factorization with Column
The QR factorization with column pivoting does not enable us to compute
a minimum norm solution to a rank-deficient linear least squares problem,
unless  . However,
by applying further orthogonal (or unitary) transformations
from the right to the upper trapezoidal matrix
. However,
by applying further orthogonal (or unitary) transformations
from the right to the upper trapezoidal matrix
 ,
using the routine xTZRQF,
,
using the routine xTZRQF,  can be eliminated:
can be eliminated:

This gives the
complete orthogonal
factorization

from which the minimum norm solution
can be obtained as

Tue Nov 29 14:03:33 EST 1994
Other Factorizations





Next:
Generalized Orthogonal Factorizations
Up:
Orthogonal Factorizations and
Previous:
Complete Orthogonal Factorization
The QL and RQ factorizations
are given by

and

These factorizations are computed by xGEQLF and xGERQF, respectively; they are
less commonly used than either the QR or LQ factorizations
described above, but have applications in, for example, the
computation of generalized QR factorizations
[2].
All the factorization routines discussed here (except xTZRQF) allow
arbitrary m and n, so that in some cases the matrices R or L are
trapezoidal rather than triangular.
A routine that performs pivoting is provided only for the QR factorization.
---------------------------------------------------------------------------
Type of
factorization Single precision Double precision
and matrix Operation real complex real complex
---------------------------------------------------------------------------
QR, general factorize with pivoting SGEQPF CGEQPF DGEQPF ZGEQPF
factorize, no pivoting SGEQRF CGEQRF DGEQRF ZGEQRF
generate Q SORGQR CUNGQR DORGQR ZUNGQR
multiply matrix by Q SORMQR CUNMQR DORMQR ZUNMQR
---------------------------------------------------------------------------
LQ, general factorize, no pivoting SGELQF CGELQF DGELQF ZGELQF
generate Q SORGLQ CUNGLQ DORGLQ ZUNGLQ
multiply matrix by Q SORMLQ CUNMLQ DORMLQ ZUNMLQ
---------------------------------------------------------------------------
QL, general factorize, no pivoting SGEQLF CGEQLF DGEQLF ZGEQLF
generate Q SORGQL CUNGQL DORGQL ZUNGQL
multiply matrix by Q SORMQL CUNMQL DORMQL ZUNMQL
---------------------------------------------------------------------------
RQ, general factorize, no pivoting SGERQF CGERQF DGERQF ZGERQF
generate Q SORGRQ CUNGRQ DORGRQ ZUNGRQ
multiply matrix by Q SORMRQ CUNMRQ DORMRQ ZUNMRQ
---------------------------------------------------------------------------
RQ, trapezoidal factorize, no pivoting STZRQF CTZRQF DTZRQF ZTZRQF
---------------------------------------------------------------------------
Table 2.9: Computational routines for orthogonal factorizations
Tue Nov 29 14:03:33 EST 1994
Generalized Orthogonal Factorizations and Linear Least Squares Problems





Next:
Generalized Factorization
Up:
Computational Routines
Previous:
Other Factorizations
Tue Nov 29 14:03:33 EST 1994
Generalized <var>QR</var> Factorization





Next:
Generalized factorization
Up:
Generalized Orthogonal Factorizations
Previous:
Generalized Orthogonal Factorizations
The generalized QR (GQR) factorization of an n-by-m matrix A and
an n-by-p matrix B is given by the pair of factorizations
A = QR and B = QTZ
where Q and Z are respectively n-by-n and p-by-p orthogonal
matrices
(or unitary matrices if A and B are complex).
R has the form:

or

where  is upper triangular. T has the form
is upper triangular. T has the form

or

where  or
or  is upper triangular.
is upper triangular.
Note that if B is square and nonsingular, the GQR factorization
of A and B implicitly gives the QR factorization of the matrix  :
:

without explicitly computing the matrix inverse  or the product
or the product  .
.
The routine xGGQRF computes the GQR
factorization by
first computing the QR factorization of A and then
the RQ factorization of  .
The orthogonal (or unitary) matrices Q and Z
can either be formed explicitly or just used to multiply another given matrix
in the same way as the
orthogonal (or unitary) matrix in the QR factorization
(see section
2.3.2).
.
The orthogonal (or unitary) matrices Q and Z
can either be formed explicitly or just used to multiply another given matrix
in the same way as the
orthogonal (or unitary) matrix in the QR factorization
(see section
2.3.2).
The GQR factorization was introduced in
[63]
[49].
The implementation of the GQR factorization here follows
[2].
Further generalizations of the GQR
factorization can be found in
[25].
The GQR factorization can be used to solve the general (Gauss-Markov) linear
model problem (GLM) (see (
2.3) and
[60][page 252]GVL2).
Using the GQR factorization of A and B, we rewrite the equation
d = Ax + By from (
2.3) as

We partition this as

where

 can be computed by xORMQR (or xUNMQR).
can be computed by xORMQR (or xUNMQR).
The GLM problem is solved by setting

from which we obtain the desired solutions

which can be computed by xTRSV, xGEMV and xORMRQ (or xUNMRQ).
Tue Nov 29 14:03:33 EST 1994
Generalized <var>RQ</var> factorization





Next:
Symmetric Eigenproblems
Up:
Generalized Orthogonal Factorizations
Previous:
Generalized Factorization
The generalized RQ (GRQ) factorization of an m-by-n matrix A and
a p-by-n matrix B is given by the pair of factorizations
A = RQ and B = ZTQ
where Q and Z are respectively n-by-n and p-by-p orthogonal
matrices (or unitary matrices if A and B are complex).
R has the form

or

where  or
or  is upper triangular. T has the form
is upper triangular. T has the form

or

where  is upper triangular.
is upper triangular.
Note that if B is square and nonsingular, the GRQ factorization of
A and B implicitly gives the RQ factorization of the matrix  :
:

without explicitly computing the matrix inverse  or the product
or the product
 .
.
The routine xGGRQF computes the GRQ factorization
by first computing the RQ factorization of A and then
the QR factorization of  .
The orthogonal (or unitary) matrices Q and Z
can either be formed explicitly or
just used to multiply another given matrix in the same way as the
orthogonal (or unitary) matrix
in the RQ factorization
(see section
2.3.2).
.
The orthogonal (or unitary) matrices Q and Z
can either be formed explicitly or
just used to multiply another given matrix in the same way as the
orthogonal (or unitary) matrix
in the RQ factorization
(see section
2.3.2).
The GRQ factorization can be used to solve the linear
equality-constrained least squares problem (LSE) (see (
2.2) and
[page 567]GVL2).
We use the GRQ factorization of B and A (note that B and A have
swapped roles), written as
B = TQ and A = ZRQ
We write the linear equality constraints Bx = d as:
TQx = d
which we partition as:

Therefore  is the solution of the upper triangular system
is the solution of the upper triangular system

Furthermore,

We partition this expression as:

where  , which
can be computed by xORMQR (or xUNMQR).
, which
can be computed by xORMQR (or xUNMQR).
To solve the LSE problem, we set

which gives  as the solution of the upper triangular system
as the solution of the upper triangular system

Finally, the desired solution is given by

which can be computed
by xORMRQ (or xUNMRQ).
Tue Nov 29 14:03:33 EST 1994
Guide





Next:
Essentials
Up:
LAPACK Users' Guide Release
Previous:
Preface to the
Tue Nov 29 14:03:33 EST 1994
Symmetric Eigenproblems





Next:
Nonsymmetric Eigenproblems
Up:
Computational Routines
Previous:
Generalized factorization
Let A be a real symmetric
or
complex Hermitian n-by-n matrix.
A scalar  is called an eigenvalue
and a nonzero column vector
z the corresponding eigenvector
if
is called an eigenvalue
and a nonzero column vector
z the corresponding eigenvector
if  .
.  is
always real when A is real symmetric or complex Hermitian.
is
always real when A is real symmetric or complex Hermitian.
The basic task of the symmetric eigenproblem routines is to compute values of  and, optionally, corresponding vectors z for a given matrix A.
and, optionally, corresponding vectors z for a given matrix A.
This computation proceeds in the following stages:
- The real symmetric or complex Hermitian matrix A is reduced to
real tridiagonal form
T.
If A is real symmetric this decomposition is
 with Q orthogonal
and T symmetric tridiagonal.
If A is complex Hermitian, the
decomposition is
with Q orthogonal
and T symmetric tridiagonal.
If A is complex Hermitian, the
decomposition is  with Q unitary and T, as before,
real symmetric tridiagonal
.
with Q unitary and T, as before,
real symmetric tridiagonal
.
- Eigenvalues and eigenvectors of the real symmetric tridiagonal matrix
T are computed.
If all eigenvalues and eigenvectors are computed, this is equivalent to
factorizing T as
 , where S is orthogonal and
, where S is orthogonal and  is diagonal.
The diagonal entries of
is diagonal.
The diagonal entries of  are the eigenvalues of T, which are also
the eigenvalues of A, and the
columns of S are the eigenvectors of T; the eigenvectors of A are
the columns of Z = QS, so that
are the eigenvalues of T, which are also
the eigenvalues of A, and the
columns of S are the eigenvectors of T; the eigenvectors of A are
the columns of Z = QS, so that  (
( when
A is complex Hermitian).
when
A is complex Hermitian).
In the real case, the decomposition  is computed by one
of the routines xSYTRD
, xSPTRD, or xSBTRD,
depending on how the matrix is
stored (see Table
2.10). The complex analogues of these routines
are called xHETRD, xHPTRD, and xHBTRD.
The routine xSYTRD (or xHETRD) represents the
matrix Q as a product of elementary reflectors,
as described in section
5.4.
The routine xORGTR
(or in the complex case xUNMTR)
is
provided to form Q explicitly;
this is needed in particular
before calling xSTEQR
to compute all the eigenvectors of A
by the QR algorithm.
The routine xORMTR
(or in the complex case xUNMTR)
is provided to multiply another matrix by Q
without forming Q explicitly; this can be used to transform
eigenvectors of T computed by xSTEIN, back to eigenvectors of A.
is computed by one
of the routines xSYTRD
, xSPTRD, or xSBTRD,
depending on how the matrix is
stored (see Table
2.10). The complex analogues of these routines
are called xHETRD, xHPTRD, and xHBTRD.
The routine xSYTRD (or xHETRD) represents the
matrix Q as a product of elementary reflectors,
as described in section
5.4.
The routine xORGTR
(or in the complex case xUNMTR)
is
provided to form Q explicitly;
this is needed in particular
before calling xSTEQR
to compute all the eigenvectors of A
by the QR algorithm.
The routine xORMTR
(or in the complex case xUNMTR)
is provided to multiply another matrix by Q
without forming Q explicitly; this can be used to transform
eigenvectors of T computed by xSTEIN, back to eigenvectors of A.
When packed storage is used, the corresponding routines for forming Q
or multiplying another matrix by Q are xOPGTR and xOPMTR
(in the complex case, xUPGTR and xUPMTR).
When A is banded and xSBTRD
(or xHBTRD)
is used to reduce it to
tridiagonal form
, Q is determined as a product of Givens rotations
, not
as a product of elementary reflectors; if Q is required, it must be formed
explicitly by the reduction routine.
xSBTRD is based on the vectorizable algorithm due to Kaufman
[57].
There are several routines for computing eigenvalues
and eigenvectors
of T,
to cover the cases of computing some or all of the eigenvalues, and some or
all of the eigenvectors. In addition, some routines run faster in some
computing environments or for some matrices than for others. Also,
some routines are more accurate than other routines.
- xSTEQR
-
This routine uses the implicitly shifted QR algorithm.
It switches between the QR and QL variants in order to
handle graded matrices more effectively than the simple QL variant that
is provided by the EISPACK routines IMTQL1 and IMTQL2. See
[46] for details.
- xSTERF
-
This routine uses a square-root free version of the QR
algorithm, also switching between QR and QL variants, and can only
compute all the eigenvalues. See
[46] for details.
- xSTEDC
-
This routine uses Cuppen's divide and conquer algorithm
to find the eigenvalues and the eigenvectors (if only eigenvalues
are desired, xSTEDC calls xSTERF). xSTEDC can be many times faster than
xSTEQR for large matrices but needs more work space (
 or
or  ).
See
[67]
[47]
[15] for details.
).
See
[67]
[47]
[15] for details.
- xPTEQR
-
This routine applies to symmetric positive definite
tridiagonal
matrices only. It uses a combination of Cholesky factorization
and bidiagonal QR iteration
(see xBDSQR) and may be significantly more accurate than the other routines.
See
[41]
[16]
[22]
[13]
for details.
- xSTEBZ
-
This routine uses bisection to compute some or all of the
eigenvalues. Options provide for computing all the eigenvalues in a real
interval or all the eigenvalues
from the i-th to the j-th largest.
It can be highly accurate, but may be adjusted to run faster if lower
accuracy is acceptable.
- xSTEIN
-
Given accurate eigenvalues, this routine uses inverse
iteration
to compute some or all of the eigenvectors.
See Table
2.10.
------------------------------------------------------------------------------
Type of matrix Single precision Double precision
and storage scheme Operation real complex real complex
------------------------------------------------------------------------------
dense symmetric tridiagonal reduction SSYTRD CHETRD DSYTRD ZHETRD
(or Hermitian)
------------------------------------------------------------------------------
packed symmetric tridiagonal reduction SSPTRD CHPTRD DSPTRD ZHPTRD
(or Hermitian)
------------------------------------------------------------------------------
band symmetric tridiagonal reduction SSBTRD CHBTRD DSBTRD ZHBTRD
(or Hermitian)
orthogonal/unitary generate matrix after SORGTR CUNGTR DORGTR ZUNGTR
reduction by xSYTRD
multiply matrix after SORMTR CUNMTR DORMTR ZUNMTR
reduction by xSYTRD
------------------------------------------------------------------------------
orthogonal/unitary generate matrix after SOPGTR CUPGTR DOPGTR ZUPGTR
(packed storage) reduction by xSPTRD
multiply matrix after SOPMTR CUPMTR DOPMTR ZUPMTR
reduction by xSPTRD
------------------------------------------------------------------------------
symmetric eigenvalues/ SSTEQR CSTEQR DSTEQR ZSTEQR
tridiagonal eigenvectors via QR
eigenvalues only SSTERF DSTERF
via root-free QR
eigenvalues only SSTEBZ DSTEBZ
via bisection
eigenvectors by SSTEIN CSTEIN DSTEIN ZSTEIN
inverse iteration
------------------------------------------------------------------------------
symmetric eigenvalues/ SPTEQR CPTEQR DPTEQR ZPTEQR
tridiagonal eigenvectors
positive definite
------------------------------------------------------------------------------
Table 2.10: Computational routines for the symmetric eigenproblem





Next:
Nonsymmetric Eigenproblems
Up:
Computational Routines
Previous:
Generalized factorization
Tue Nov 29 14:03:33 EST 1994
Nonsymmetric Eigenproblems





Next:
EigenvaluesEigenvectors and
Up:
Computational Routines
Previous:
Symmetric Eigenproblems
Tue Nov 29 14:03:33 EST 1994
Eigenvalues, Eigenvectors and Schur Factorization





Next:
Balancing
Up:
Nonsymmetric Eigenproblems
Previous:
Nonsymmetric Eigenproblems
Let A be a square n-by-n matrix. A scalar  is called
an eigenvalue
and a non-zero column vector v the corresponding
right eigenvector
if
is called
an eigenvalue
and a non-zero column vector v the corresponding
right eigenvector
if  . A nonzero column vector u
satisfying
. A nonzero column vector u
satisfying  is called the left eigenvector
.
The first basic task
of the routines described in this section
is to compute, for a given matrix A, all n values of
is called the left eigenvector
.
The first basic task
of the routines described in this section
is to compute, for a given matrix A, all n values of  and,
if desired, their associated right eigenvectors v and/or
left eigenvectors u.
and,
if desired, their associated right eigenvectors v and/or
left eigenvectors u.
A second basic task is to compute the Schur factorization of a matrix A.
If A is complex, then its Schur factorization is  , where
Z is unitary and T is upper triangular. If A is real, its
Schur factorization is
, where
Z is unitary and T is upper triangular. If A is real, its
Schur factorization is  , where Z is orthogonal.
and T is upper quasi-triangular (1-by-1 and 2-by-2 blocks on
its diagonal).
The columns of Z are called the Schur vectors of A.
The eigenvalues of A appear on the diagonal of T; complex conjugate
eigenvalues of a real A correspond to 2-by-2 blocks on the diagonal of T.
, where Z is orthogonal.
and T is upper quasi-triangular (1-by-1 and 2-by-2 blocks on
its diagonal).
The columns of Z are called the Schur vectors of A.
The eigenvalues of A appear on the diagonal of T; complex conjugate
eigenvalues of a real A correspond to 2-by-2 blocks on the diagonal of T.
These two basic tasks can be performed in the following stages:
- A general matrix A is reduced to upper Hessenberg form
H
which is zero below the first subdiagonal. The reduction may be written
 with Q orthogonal if A is real, or
with Q orthogonal if A is real, or
 with Q unitary if A is complex.
The reduction is performed by subroutine xGEHRD, which
represents
Q in a factored form, as described in section
5.4.
The routine xORGHR (or in the complex case xUNGHR) is provided to
form Q explicitly.
The routine xORMHR
(or in the complex case xUNMHR) is provided to
multiply another matrix by Q without forming Q explicitly.
with Q unitary if A is complex.
The reduction is performed by subroutine xGEHRD, which
represents
Q in a factored form, as described in section
5.4.
The routine xORGHR (or in the complex case xUNGHR) is provided to
form Q explicitly.
The routine xORMHR
(or in the complex case xUNMHR) is provided to
multiply another matrix by Q without forming Q explicitly.
- The upper Hessenberg matrix H is reduced to Schur form T,
giving the Schur factorization
 (for H real) or
(for H real) or  (for H complex). The matrix A (the Schur vectors
of H) may
optionally be computed as well. Alternatively S may be postmultiplied
into the matrix Q determined in stage 1, to give the matrix Z = QS, the
Schur vectors of A. The eigenvalues
are obtained from the
diagonal of T. All this is done by subroutine xHSEQR.
(for H complex). The matrix A (the Schur vectors
of H) may
optionally be computed as well. Alternatively S may be postmultiplied
into the matrix Q determined in stage 1, to give the matrix Z = QS, the
Schur vectors of A. The eigenvalues
are obtained from the
diagonal of T. All this is done by subroutine xHSEQR.
- Given the eigenvalues, the eigenvectors may be computed in
two different ways. xHSEIN performs inverse iteration
on H to compute
the eigenvectors of H;
xORMHR
can then be used to multiply the eigenvectors by the matrix Q
in order to transform them to eigenvectors of A.
xTREVC
computes the eigenvectors of T, and optionally transforms them
to those of H or A if the matrix S or Z is supplied.
Both xHSEIN and xTREVC allow selected left and/or right eigenvectors
to be computed.
Other subsidiary tasks may be performed before or after those just described.





Next:
Balancing
Up:
Nonsymmetric Eigenproblems
Previous:
Nonsymmetric Eigenproblems
Tue Nov 29 14:03:33 EST 1994
Balancing





Next:
Invariant Subspaces and
Up:
Nonsymmetric Eigenproblems
Previous:
EigenvaluesEigenvectors and
The routine xGEBAL
may be used to balance the
matrix A prior to reduction to Hessenberg form
. Balancing involves two
steps, either of which is optional:
- first, xGEBAL
attempts to permute A by a similarity transformation
to
block upper triangular form:

where P is a permutation matrix and  and
and  are
upper triangular.
Thus the matrix is already in Schur form
outside the
central diagonal block
are
upper triangular.
Thus the matrix is already in Schur form
outside the
central diagonal block  in rows and columns ILO to IHI.
Subsequent operations by xGEBAL, xGEHRD or xHSEQR need only be applied to
these rows and columns; therefore ILO and IHI are passed as arguments to
xGEHRD
and
xHSEQR
. This can save a significant amount of
work if ILO > 1 or IHI < n.
If no suitable permutation can be found (as is very often the case),
xGEBAL sets ILO = 1 and IHI = n, and
in rows and columns ILO to IHI.
Subsequent operations by xGEBAL, xGEHRD or xHSEQR need only be applied to
these rows and columns; therefore ILO and IHI are passed as arguments to
xGEHRD
and
xHSEQR
. This can save a significant amount of
work if ILO > 1 or IHI < n.
If no suitable permutation can be found (as is very often the case),
xGEBAL sets ILO = 1 and IHI = n, and  is
the whole of A.
is
the whole of A.
- secondly, xGEBAL applies a diagonal similarity transformation to
 to make the rows and columns of
to make the rows and columns of  as close in norm in possible:
as close in norm in possible:
This can improve the
accuracy of later processing in some cases; see subsection
4.8.1.2.
If A was balanced by xGEBAL, then eigenvectors computed by subsequent
operations are eigenvectors of the balanced matrix  ;
xGEBAK
must then be called
to transform them back to eigenvectors of the original matrix A.
;
xGEBAK
must then be called
to transform them back to eigenvectors of the original matrix A.
Tue Nov 29 14:03:33 EST 1994
Invariant Subspaces and Condition Numbers





Next:
Singular Value Decomposition
Up:
Nonsymmetric Eigenproblems
Previous:
Balancing
The Schur form
depends on the order of the eigenvalues on the diagonal
of T and this may optionally be chosen by the user. Suppose the user chooses
that  ,
,
1 < = j < = n, appear in the upper left
corner of T. Then the first j columns of Z span the right invariant
subspace of A corresponding to  .
.
The following routines perform this re-ordering and also
compute condition numbers for eigenvalues, eigenvectors,
and invariant subspaces:
- xTREXC
will move an eigenvalue (or 2-by-2 block) on the diagonal of
the Schur form
from its original position to any other position. It may be used to
choose the order in which eigenvalues appear in the Schur form.
- xTRSYL
solves
the Sylvester matrix equation
 for A, given
matrices A, B and C, with A and B (quasi) triangular.
It is used in the routines xTRSNA and xTRSEN, but it is also of independent
interest.
for A, given
matrices A, B and C, with A and B (quasi) triangular.
It is used in the routines xTRSNA and xTRSEN, but it is also of independent
interest.
- xTRSNA
computes the condition numbers of the eigenvalues and/or
right eigenvectors of a matrix T in Schur form.
These are the same as the condition
numbers of the eigenvalues and right eigenvectors of the original matrix
A from which T is derived. The user may compute these condition numbers
for all eigenvalue/eigenvector pairs, or for any selected subset.
For more details, see section
4.8 and
[11].
- xTRSEN
moves
a selected subset of the eigenvalues of a matrix T
in Schur form to the upper left corner of T, and optionally computes
the condition numbers
of their average value and of their right
invariant subspace. These are the same as the condition numbers of the
average eigenvalue and right invariant subspace of the original matrix A
from which T is derived.
For more details, see section
4.8 and
[11]
See Table
2.11 for a complete list of the routines.
-----------------------------------------------------------------------------
Type of matrix Single precision Double precision
and storage scheme Operation real complex real complex
-----------------------------------------------------------------------------
general Hessenberg reduction SGEHRD CGEHRD DGEHRD ZGEHRD
balancing SGEBAL CGEBAL DGEBAL ZGEBAL
backtransforming SGEBAK CGEBAK DGEBAK ZGEBAK
-----------------------------------------------------------------------------
orthogonal/unitary generate matrix after SORGHR CUNGHR DORGHR ZUNGHR
Hessenberg reduction
multiply matrix after SORMHR CUNMHR DORMHR ZUNMHR
Hessenberg reduction
-----------------------------------------------------------------------------
Hessenberg Schur factorization SHSEQR CHSEQR DHSEQR ZHSEQR
eigenvectors by SHSEIN CHSEIN DHSEIN ZHSEIN
inverse iteration
-----------------------------------------------------------------------------
(quasi)triangular eigenvectors STREVC CTREVC DTREVC ZTREVC
reordering Schur STREXC CTREXC DTREXC ZTREXC
factorization
Sylvester equation STRSYL CTRSYL DTRSYL ZTRSYL
condition numbers of STRSNA CTRSNA DTRSNA ZTRSNA
eigenvalues/vectors
condition numbers of STRSEN CTRSEN DTRSEN ZTRSEN
eigenvalue cluster/
invariant subspace
-----------------------------------------------------------------------------
Table 2.11: Computational routines for the nonsymmetric eigenproblem





Next:
Singular Value Decomposition
Up:
Nonsymmetric Eigenproblems
Previous:
Balancing
Tue Nov 29 14:03:33 EST 1994
Singular Value Decomposition





Next:
Generalized Symmetric Definite
Up:
Computational Routines
Previous:
Invariant Subspaces and
Let A be a general real m-by-n matrix. The singular value
decomposition (SVD) of A is the factorization
 , where
U and V are orthogonal, and
, where
U and V are orthogonal, and
 , r = min(m , n),
with
, r = min(m , n),
with  . If A is complex, then
its SVD is
. If A is complex, then
its SVD is  where U and V are unitary,
and
where U and V are unitary,
and  is as before with real
diagonal elements.
The
is as before with real
diagonal elements.
The  are called the singular values
,
the first r columns of V
the right singular vectors
and
the first r columns of U
the left singular vectors
.
are called the singular values
,
the first r columns of V
the right singular vectors
and
the first r columns of U
the left singular vectors
.
The routines described in this section, and listed in Table
2.12,
are used to compute this decomposition.
The computation proceeds in the following stages:
- The matrix A is reduced to bidiagonal
form:
 if
A is real (
if
A is real ( if A is complex), where
if A is complex), where  and
and  are orthogonal (unitary if A is complex), and B is real and
upper-bidiagonal when m > = n and lower bidiagonal when m < n, so
that B is nonzero only on the main diagonal and either on the first
superdiagonal (if m > = n) or the first subdiagonal (if m < n).
are orthogonal (unitary if A is complex), and B is real and
upper-bidiagonal when m > = n and lower bidiagonal when m < n, so
that B is nonzero only on the main diagonal and either on the first
superdiagonal (if m > = n) or the first subdiagonal (if m < n).
- The SVD of the bidiagonal matrix B is computed:
 ,
where
,
where  and
and  are orthogonal and
are orthogonal and  is diagonal as described
above. The singular vectors of A are then
is diagonal as described
above. The singular vectors of A are then  and
and
 .
.
The reduction to bidiagonal form is performed by the subroutine xGEBRD,
or by xGBBRD
for a band matrix.
The routine xGEBRD represents
 and
and  in factored form as products of elementary reflectors,
as described in section
5.4.
If A is real,
the matrices
in factored form as products of elementary reflectors,
as described in section
5.4.
If A is real,
the matrices  and
and  may be computed explicitly using routine xORGBR,
or multiplied by other matrices without forming
may be computed explicitly using routine xORGBR,
or multiplied by other matrices without forming  and
and  using routine xORMBR
.
If A is complex, one instead uses xUNGBR
and xUNMBR
, respectively.
using routine xORMBR
.
If A is complex, one instead uses xUNGBR
and xUNMBR
, respectively.
If A is banded and xGBBRD is used to reduce it to bidiagonal form,
 and
and  are determined as products of Givens rotations
, rather than
as products of elementary reflectors. If
are determined as products of Givens rotations
, rather than
as products of elementary reflectors. If  or
or  is required, it
must be formed explicitly by xGBBRD. xGBBRD uses a vectorizable
algorithm, similar to that used by xSBTRD (see Kaufman
[57]).
xGBBRD may be much faster than xGEBRD when the bandwidth is narrow.
is required, it
must be formed explicitly by xGBBRD. xGBBRD uses a vectorizable
algorithm, similar to that used by xSBTRD (see Kaufman
[57]).
xGBBRD may be much faster than xGEBRD when the bandwidth is narrow.
The SVD of the bidiagonal matrix is computed by the subroutine xBDSQR.
xBDSQR is more accurate than its counterparts in LINPACK and EISPACK:
barring underflow and overflow, it computes all the singular values of
A to nearly full relative precision, independent of their magnitudes.
It also computes the singular vectors much more accurately. See
section
4.9 and
[41]
[16]
[22] for details.
If m >> n, it may be more efficient to first perform a QR factorization
of A, using the routine xGEQRF
,
and then to compute the SVD of the n-by-n matrix R, since
if A = QR and  , then the SVD of A is given by
, then the SVD of A is given by
 .
Similarly, if m << n, it may be more efficient to first perform an
LQ factorization of A, using xGELQF. These preliminary QR and LQ
factorizations are performed by the driver xGESVD.
.
Similarly, if m << n, it may be more efficient to first perform an
LQ factorization of A, using xGELQF. These preliminary QR and LQ
factorizations are performed by the driver xGESVD.
The SVD may be used to find a minimum norm solution
to a (possibly)
rank-deficient linear least squares
problem (
2.1). The effective rank, k, of A can be determined as the
number of singular values which exceed a suitable threshold.
Let  be the leading k-by-k submatrix of
be the leading k-by-k submatrix of  , and
, and
 be the matrix consisting of the first k columns of V.
Then the solution is given by:
be the matrix consisting of the first k columns of V.
Then the solution is given by:

where  consists of the first k elements of
consists of the first k elements of  .
.  can be computed using xORMBR, and
xBDSQR has an option to multiply a vector by
can be computed using xORMBR, and
xBDSQR has an option to multiply a vector by  .
.
-----------------------------------------------------------------------------
Type of matrix Single precision Double precision
and storage scheme Operation real complex real complex
-----------------------------------------------------------------------------
general bidiagonal reduction SGEBRD CGEBRD DGEBRD ZGEBRD
-----------------------------------------------------------------------------
general band bidiagonal reduction SGBBRD CGBBRD DGBBRD ZGBBRD
-----------------------------------------------------------------------------
orthogonal/unitary generate matrix after SORGBR CUNGBR DORGBR ZUNGBR
bidiagonal reduction
multiply matrix after SORMBR CUNMBR DORMBR ZUNMBR
bidiagonal reduction
-----------------------------------------------------------------------------
bidiagonal singular values/ SBDSQR CBDSQR DBDSQR ZBDSQR
singular vectors
-----------------------------------------------------------------------------
Table 2.12: Computational routines for the singular value decomposition





Next:
Generalized Symmetric Definite
Up:
Computational Routines
Previous:
Invariant Subspaces and
Tue Nov 29 14:03:33 EST 1994
Generalized Symmetric Definite Eigenproblems





Next:
Generalized Nonsymmetric Eigenproblems
Up:
Computational Routines
Previous:
Singular Value Decomposition
This section is concerned with the solution of the generalized eigenvalue
problems  ,
,  , and
, and  , where
A and B are real symmetric or complex Hermitian and B is positive definite.
Each of these problems can be reduced to a standard symmetric
eigenvalue problem, using a Cholesky factorization of B as either
, where
A and B are real symmetric or complex Hermitian and B is positive definite.
Each of these problems can be reduced to a standard symmetric
eigenvalue problem, using a Cholesky factorization of B as either
 or
or  (
( or
or  in the Hermitian case).
In the case
in the Hermitian case).
In the case  , if A and B are banded then this may also
be exploited to get a faster algorithm.
, if A and B are banded then this may also
be exploited to get a faster algorithm.
With  , we have
, we have

Hence the eigenvalues of  are those of
are those of  ,
where C is the symmetric matrix
,
where C is the symmetric matrix  and
and  .
In the complex case C is Hermitian with
.
In the complex case C is Hermitian with  and
and  .
.
Table
2.13 summarizes how each of the three types of problem
may be reduced to standard form  , and how the eigenvectors z
of the original problem may be recovered from the eigenvectors y of the
reduced problem. The table applies to real problems; for complex problems,
transposed matrices must be replaced by conjugate-transposes.
, and how the eigenvectors z
of the original problem may be recovered from the eigenvectors y of the
reduced problem. The table applies to real problems; for complex problems,
transposed matrices must be replaced by conjugate-transposes.

Table 2.13: Reduction of generalized symmetric definite eigenproblems to standard
problems
Given A and a Cholesky factorization of B,
the routines xyyGST overwrite A
with the matrix C of the corresponding standard problem
 (see Table
2.14).
This may then be solved using the routines described in
subsection
2.3.4.
No special routines are needed
to recover the eigenvectors z of the generalized problem from
the eigenvectors y of the standard problem, because these
computations are simple applications of Level 2 or Level 3 BLAS.
(see Table
2.14).
This may then be solved using the routines described in
subsection
2.3.4.
No special routines are needed
to recover the eigenvectors z of the generalized problem from
the eigenvectors y of the standard problem, because these
computations are simple applications of Level 2 or Level 3 BLAS.
If the problem is  and the matrices A and B are banded,
the matrix C as defined above is, in general, full.
We can reduce the problem to a banded standard problem by modifying the
definition of C thus:
and the matrices A and B are banded,
the matrix C as defined above is, in general, full.
We can reduce the problem to a banded standard problem by modifying the
definition of C thus:

where Q is an orthogonal matrix chosen to ensure that C has bandwidth
no greater than that of A.
Q is determined as a product of Givens rotations.
This is known as Crawford's algorithm
(see Crawford
[14]).
If X is required, it must be formed explicitly by the reduction routine.
A further refinement is possible when A and B are banded, which halves
the amount of work required to form C (see Wilkinson
[79]).
Instead of the standard Cholesky factorization of B as  or
or  ,
we use a ``split Cholesky'' factorization
,
we use a ``split Cholesky'' factorization  (
( if B is complex), where:
if B is complex), where:

with  upper triangular and
upper triangular and  lower triangular of
order approximately n / 2;
S has the same bandwidth as B. After B has been factorized in this way
by the routine
xPBSTF
,
the reduction of the banded generalized
problem
lower triangular of
order approximately n / 2;
S has the same bandwidth as B. After B has been factorized in this way
by the routine
xPBSTF
,
the reduction of the banded generalized
problem  to a banded standard problem
to a banded standard problem  is performed by the routine xSBGST
(or xHBGST
for complex matrices).
This routine implements a vectorizable form of the algorithm, suggested by
Kaufman
[57].
is performed by the routine xSBGST
(or xHBGST
for complex matrices).
This routine implements a vectorizable form of the algorithm, suggested by
Kaufman
[57].
--------------------------------------------------------------------
Type of matrix Single precision Double precision
and storage scheme Operation real complex real complex
--------------------------------------------------------------------
symmetric/Hermitian reduction SSYGST CHEGST DSYGST ZHEGST
--------------------------------------------------------------------
symmetric/Hermitian reduction SSPGST CHPGST DSPGST ZHPGST
(packed storage)
--------------------------------------------------------------------
symmetric/Hermitian split SPBSTF CPBSTF DPBSTF ZPBSTF
banded Cholesky
factorization
--------------------------------------------------------------------
reduction SSBGST DSBGST CHBGST ZHBGST
--------------------------------------------------------------------
Table 2.14: Computational routines for the generalized symmetric definite eigenproblem





Next:
Generalized Nonsymmetric Eigenproblems
Up:
Computational Routines
Previous:
Singular Value Decomposition
Tue Nov 29 14:03:33 EST 1994
Generalized Nonsymmetric Eigenproblems





Next:
Generalized (or Quotient)
Up:
Computational Routines
Previous:
Generalized Symmetric Definite
Let A and B be n-by-n matrices.
A scalar  is called a generalized eigenvalue
and a
non-zero column vector x the corresponding right generalized eigenvector
if
is called a generalized eigenvalue
and a
non-zero column vector x the corresponding right generalized eigenvector
if  .
A non-zero column vector y satisfying
.
A non-zero column vector y satisfying  (where the superscript H denotes conjugate-transpose)
is called
the left generalized eigenvector
corresponding to
(where the superscript H denotes conjugate-transpose)
is called
the left generalized eigenvector
corresponding to  .
(For simplicity,
we will usually omit the word ``generalized'' when no confusion
is likely to arise.)
If B is singular, we can have the infinite eigenvalue
.
(For simplicity,
we will usually omit the word ``generalized'' when no confusion
is likely to arise.)
If B is singular, we can have the infinite eigenvalue
 , by which we mean
Bx = 0.
Note that if A is non-singular, then the equivalent problem
, by which we mean
Bx = 0.
Note that if A is non-singular, then the equivalent problem
 is perfectly well-behaved, and the infinite eigenvalue
corresponds to
is perfectly well-behaved, and the infinite eigenvalue
corresponds to  .
To deal with infinite eigenvalues,
the LAPACK routines return two values,
.
To deal with infinite eigenvalues,
the LAPACK routines return two values,
 and
and  ,
for each eigenvalue
,
for each eigenvalue  .
The first basic task of these routines is to compute the
all n pairs
.
The first basic task of these routines is to compute the
all n pairs  and x and/or y for a given
pair of matrices A,B.
and x and/or y for a given
pair of matrices A,B.
If the determinant of  is zero for all values of
is zero for all values of  ,
the eigenvalue problem is called singular, and is signaled by some
,
the eigenvalue problem is called singular, and is signaled by some
 (in the presence of roundoff,
(in the presence of roundoff,  and
and  may
be very small). In this case the eigenvalue problem is very ill-conditioned,
and in fact some of the other nonzero values of
may
be very small). In this case the eigenvalue problem is very ill-conditioned,
and in fact some of the other nonzero values of  and
and  may be
indeterminate
[43]
[21]
[80]
[71].
may be
indeterminate
[43]
[21]
[80]
[71].
The other basic task is to compute the
generalized Schur decomposition of the pair A,B.
If A and B are complex,
then the pair's generalized Schur decomposition is
 , where Q and Z are unitary and
S and P are upper triangular.
The LAPACK routines normalize P
to have
non-negative diagonal entries. Note that in this form,
the eigenvalues can be easily computed from the diagonals:
, where Q and Z are unitary and
S and P are upper triangular.
The LAPACK routines normalize P
to have
non-negative diagonal entries. Note that in this form,
the eigenvalues can be easily computed from the diagonals:
 ,
and so the LAPACK routines return
,
and so the LAPACK routines return
 and
and  . The generalized Schur
form depends on the order on which the eigenvalues appear on the
diagonal. In a future version of LAPACK, we will supply routines
to allow the user to choose this order.
. The generalized Schur
form depends on the order on which the eigenvalues appear on the
diagonal. In a future version of LAPACK, we will supply routines
to allow the user to choose this order.
If A and B are real,
then the pair's generalized Schur decomposition is
 ,
,  ,
where Q and Z are orthogonal,
P is upper triangular,
and S is quasi-upper triangular
with 1-by-1 and 2-by-2 blocks on the diagonal.
The 1-by-1 blocks correspond to real generalized eigenvalues,
while the 2-by-2 blocks correspond to complex conjugate
pairs of generalized eigenvalues.
In this case, P
is normalized so that diagonal
entries of P
corresponding to 1-by-1 blocks of S are non-negative,
while the (upper triangular) diagonal blocks of P corresponding
to 2-by-2 blocks of S are made diagonal.
Note that for real eigenvalues,
as for all eigenvalues in the complex case,
the
,
where Q and Z are orthogonal,
P is upper triangular,
and S is quasi-upper triangular
with 1-by-1 and 2-by-2 blocks on the diagonal.
The 1-by-1 blocks correspond to real generalized eigenvalues,
while the 2-by-2 blocks correspond to complex conjugate
pairs of generalized eigenvalues.
In this case, P
is normalized so that diagonal
entries of P
corresponding to 1-by-1 blocks of S are non-negative,
while the (upper triangular) diagonal blocks of P corresponding
to 2-by-2 blocks of S are made diagonal.
Note that for real eigenvalues,
as for all eigenvalues in the complex case,
the  and
and  values corresponding to real eigenvalues
may be easily computed from the diagonal of S and P.
The
values corresponding to real eigenvalues
may be easily computed from the diagonal of S and P.
The  and
and  values corresponding to complex
eigenvalues are computed by computing
values corresponding to complex
eigenvalues are computed by computing  ,
then computing the
,
then computing the  values that would result if
the 2-by-2 diagonal block of S,P were upper triangularized using
unitary transformations
,
and finally multiplying to get
values that would result if
the 2-by-2 diagonal block of S,P were upper triangularized using
unitary transformations
,
and finally multiplying to get  and
and  .
.
The columns of Q and Z are called generalized Schur vectors
and span pairs of deflating subspaces of A and B
[72].
Deflating subspaces are a generalization of invariant subspaces:
The first k columns of Z span a right deflating subspace
mapped by both A and B into a left deflating subspace spanned by
the first k columns of Q. This pair of deflating subspaces corresponds
to the first k eigenvalues appearing at the top of S and p.
The computations proceed in the following stages:
- The pair A,B is reduced to generalized upper Hessenberg form.
If A and B are real this decomposition is
 ,
,  where H is upper Hessenberg (zero below the first subdiagonal), T is
upper triangular and U and V are orthogonal. If A and B are complex,
the decomposition is
where H is upper Hessenberg (zero below the first subdiagonal), T is
upper triangular and U and V are orthogonal. If A and B are complex,
the decomposition is  ,
,  with U and V unitary and
H and T as before.
This decomposition is performed by the subroutine xGGHRD,
which computes H and T and optionally U and/or V.
Note that in contrast to xGEHRD (for the standard
nonsymmetric eigenvalue problem),
xGGHRD does not compute U and V in a factored form.
with U and V unitary and
H and T as before.
This decomposition is performed by the subroutine xGGHRD,
which computes H and T and optionally U and/or V.
Note that in contrast to xGEHRD (for the standard
nonsymmetric eigenvalue problem),
xGGHRD does not compute U and V in a factored form.
- The pair H,T is reduced to generalized Schur form
 ,
,  (for H and T real) or
(for H and T real) or
 ,
,  (for H and T complex) by subroutine xHGEQZ.
The values
(for H and T complex) by subroutine xHGEQZ.
The values  and
and  are also computed.
The matrices Z and Q are optionally computed.
are also computed.
The matrices Z and Q are optionally computed.
- The left and/or right eigenvectors of the pair A
are computed by xTGEVC.
One may optionally transform the right eigenvectors of S,P
to the right eigenvectors of A,B (or of H,T) by passing
UQ,VZ (or Q,Z) to xTGEVC.
In addition, the routines xGGBAL and xGGBAK
may be used to balance the
pair A,B prior to reduction to generalized Hessenberg form.
Balancing involves
premultiplying A and B by one permutation
and postmultiplying them by another,
to try to make A,B as nearly triangular
as possible,
and then ``scaling'' the matrices by
premultiplying A and B by one diagonal
matrix and postmultiplying by another in order to
make the rows and columns of A and B
as close in norm to 1 as possible.
These transformations can improve speed and
accuracy of later processing in some cases;
however, the scaling step can sometimes make
things worse.
Moreover,
the scaling step will significantly change the generalized
Schur form
that results.
xGGBAL performs the balancing,
and xGGBAK back transforms the eigenvectors of the balanced matrix pair.
--------------------------------------------------------------------------
Type of matrix Single precision Double precision
and storage scheme Operation real complex real complex
--------------------------------------------------------------------------
general Hessenberg reduction SGGHRD CGGHRD DGGHRD ZGGHRD
balancing SGGBAL CGGBAL DGGBAL ZGGBAL
back transforming SGGBAK CGGBAK DGGBAK ZGGBAK
--------------------------------------------------------------------------
Hessenberg Schur factorization SHGEQZ CHGEQZ DHGEQZ ZHGEQZ
--------------------------------------------------------------------------
(quasi)triangular eigenvectors STGEVC CTGEVC DTGEVC ZTGEVC
--------------------------------------------------------------------------
Table 2.15: Computational routines for the generalized nonsymmetric eigenproblem
A future release of LAPACK will include the routines xTGEXC, xTGSYL, xTGSNA
and xTGSEN, which are analogous to the routines xTREXC, xTRSYL, xTRSNA and
xTRSEN. They will
reorder eigenvalues in generalized Schur form, solve the generalized
Sylvester equation, compute condition numbers of generalized eigenvalues and
eigenvectors, and compute condition numbers of average eigenvalues and deflating
subspaces.





Next:
Generalized (or Quotient)
Up:
Computational Routines
Previous:
Generalized Symmetric Definite
Tue Nov 29 14:03:33 EST 1994
Generalized (or Quotient) Singular Value Decomposition





Next:
Performance of LAPACK
Up:
Computational Routines
Previous:
Generalized Nonsymmetric Eigenproblems
The generalized (or quotient) singular value decomposition
of an m-by-n matrix A and a p-by-n matrix B is described
in section
2.2.5.
The routines described in this section, are used
to compute the decomposition. The computation proceeds in the following
two stages:
- xGGSVP
is used to reduce the matrices A and B to triangular form:

where  and
and  are nonsingular upper triangular, and
are nonsingular upper triangular, and
 is upper triangular.
If m - k - 1 < 0, the bottom zero block of
is upper triangular.
If m - k - 1 < 0, the bottom zero block of  does not appear,
and
does not appear,
and  is upper trapezoidal.
is upper trapezoidal.
 ,
,  and
and  are
orthogonal matrices (or unitary matrices if A and B are complex).
l is the rank of B, and
k + l is the rank of
are
orthogonal matrices (or unitary matrices if A and B are complex).
l is the rank of B, and
k + l is the rank of  .
.
- The generalized singular value decomposition of two l-by-l
upper triangular matrices
 and
and  is computed using
xTGSJA
is computed using
xTGSJA
 :
:

Here  ,
,  and
and  are orthogonal (or unitary) matrices,
C and S are both real
nonnegative diagonal matrices satisfying
are orthogonal (or unitary) matrices,
C and S are both real
nonnegative diagonal matrices satisfying  , S is nonsingular,
and R is upper triangular and nonsingular.
, S is nonsingular,
and R is upper triangular and nonsingular.
--------------------------------------------------------
Single precision Double precision
Operation real complex real complex
--------------------------------------------------------
triangular reduction SGGSVP CGGSVP DGGSVP ZGGSVP
of A and B
--------------------------------------------------------
GSVD of a pair of STGSJA CTGSJA DTGSJA ZTGSJA
triangular matrices
--------------------------------------------------------
Table 2.16: Computational routines for the generalized singular value decomposition
The reduction to triangular form, performed by
xGGSVP, uses QR decomposition with column pivoting
for numerical rank determination. See
[12] for details.
The generalized singular value decomposition of two
triangular matrices, performed by xTGSJA, is done
using a Jacobi-like method as described in
[10]
[62].
Tue Nov 29 14:03:33 EST 1994
Performance of LAPACK





Next:
Factors that Affect
Up:
Guide
Previous:
Generalized (or Quotient)
Note: this chapter presents some performance figures for LAPACK
routines. The figures are provided for illustration only, and should not
be regarded as a definitive up-to-date statement of performance.
They have been selected from
performance figures obtained in 1994 during the development of version
2.0 of LAPACK. All reported timings were obtained using the optimized
version of the BLAS available on each machine. For the IBM computers,
the ESSL BLAS were used.
Performance is affected by many factors that may change from time to time,
such as details of hardware
(cycle time, cache size), compiler, and BLAS.
To obtain up-to-date performance figures, use the timing programs
provided with LAPACK.
Tue Nov 29 14:03:33 EST 1994
Essentials





Next:
LAPACK
Up:
Guide
Previous:
Guide
Tue Nov 29 14:03:33 EST 1994
Factors that Affect Performance





Next:
Vectorization
Up:
Performance of LAPACK
Previous:
Performance of LAPACK
Can we provide portable
software for computations in dense linear algebra
that is efficient on a wide range of modern high-performance computers?
If so, how?
Answering these questions - and providing
the desired software - has been the goal of the LAPACK project.
LINPACK
[26]
and EISPACK
[44]
[70] have for many years provided
high-quality portable software for linear algebra; but
on modern high-performance computers they often
achieve only a small fraction of the peak performance of the machines.
Therefore, LAPACK has been designed to supersede LINPACK and EISPACK,
principally by achieving much greater efficiency - but at the same time
also adding extra functionality, using some new or improved algorithms,
and integrating the two sets of algorithms into a single package.
LAPACK was originally targeted to achieve good performance on single-processor
vector machines and on shared memory multiprocessor
machines
with a modest
number of powerful processors. Since the start of the project,
another class of machines has
emerged for which LAPACK software is equally well-suited-the high-performance
``super-scalar'' workstations
.
(LAPACK is intended to be used across the whole spectrum of modern computers,
but when considering performance, the emphasis is on machines at the more
powerful end of the spectrum.)
Here we discuss the main factors that affect the performance of linear
algebra software on these classes of machines.
Tue Nov 29 14:03:33 EST 1994
Vectorization





Next:
Data Movement
Up:
Factors that Affect
Previous:
Factors that Affect
Designing vectorizable algorithms in linear algebra is usually straightforward.
Indeed, for many computations there are several variants, all vectorizable, but
with different characteristics in performance (see, for example,
[33]).
Linear algebra algorithms can come close to the peak performance of
many machines - principally because peak performance depends on some form of
chaining of vector addition and multiplication operations, and this is just
what the algorithms require.
However, when the algorithms are realized in straightforward Fortran 77 code,
the performance may fall well short of the expected level, usually because
vectorizing Fortran compilers fail to minimize the number of memory references
- that is, the number of vector load and store operations. This brings us to
the next factor.
Tue Nov 29 14:03:33 EST 1994
Data Movement





Next:
Parallelism
Up:
Factors that Affect
Previous:
Vectorization
What often limits the actual performance of a vector-or scalar-
floating-point unit is the rate of transfer of data between different levels
of memory in the machine. Examples include: the transfer of vector operands
in and out of vector registers
, the transfer of
scalar operands in and out of a
high-speed scalar processor, the movement of data between main memory and a
high-speed cache
or local memory
, and paging between
actual memory and disk storage in a virtual memory system.
It is desirable to maximize the ratio of floating-point operations to memory
references, and to re-use data as much as possible while it is stored in the
higher levels of the memory hierarchy (for example, vector registers or
high-speed cache).
A Fortran programmer has no explicit control over these types of data movement,
although one can often influence them by imposing a suitable structure on an
algorithm.
Tue Nov 29 14:03:33 EST 1994
Parallelism





Next:
The BLAS as
Up:
Factors that Affect
Previous:
Data Movement
The nested loop structure of most linear algebra algorithms offers
considerable scope for loop-based parallelism on shared memory
machines. This is the principal type of parallelism that LAPACK at present
aims to exploit.
It can sometimes be generated automatically
by a compiler, but often requires the insertion of compiler directives
.
Tue Nov 29 14:03:33 EST 1994
The BLAS as the Key to Portability





Next:
Block Algorithms and
Up:
Performance of LAPACK
Previous:
Parallelism
How then can we hope to be able to achieve sufficient control over
vectorization, data movement, and parallelism in portable Fortran code,
to obtain the levels of performance that machines can offer?
The LAPACK strategy for combining
efficiency with portability
is to construct the software as much as possible
out of calls to the BLAS (Basic Linear Algebra Subprograms); the BLAS are used
as building blocks.
The efficiency
of LAPACK software depends on efficient implementations
of the BLAS being provided by computer vendors (or others) for their machines.
Thus the BLAS form a low-level interface between LAPACK software and
different machine architectures.
Above this level, almost all of the LAPACK software is truly portable.
There are now three levels of BLAS:
- Level 1 BLAS
[58]:
- for vector operations, such as

- Level 2 BLAS
[30]:
- for matrix-vector operations, such as

- Level 3 BLAS
[28]:
- for matrix-matrix operations, such as

Here, A, B and C are matrices, x and y are vectors, and  and
and
 are scalars.
are scalars.
The Level 1 BLAS
are used in LAPACK,
but for convenience rather than
for performance: they perform an insignificant fraction of the computation,
and they cannot achieve high efficiency on most modern supercomputers.
The Level 2 BLAS
can achieve near-peak performance
on many vector processors,
such as a single processor of a CRAY Y-MP, CRAY C90, or CONVEX C4 machine.
However on other vector processors, such as a CRAY 2,
or a RISC workstation,
their performance is limited by the rate of data movement between different
levels of memory.
This limitation is overcome by the Level 3 BLAS
,
which perform  floating-point operations on
floating-point operations on  data, whereas the Level 2 BLAS
perform only
data, whereas the Level 2 BLAS
perform only  operations on
operations on  data.
data.
The BLAS also allow us to exploit parallelism in a way that is transparent
to the software that calls them.
Even the Level 2 BLAS offer some scope for exploiting parallelism, but greater
scope is provided by the Level 3 BLAS, as Table
3.1 illustrates.

Table 3.1: Speed in megaflops of Level 2 and Level 3 BLAS operations on a
CRAY C90





Next:
Block Algorithms and
Up:
Performance of LAPACK
Previous:
Parallelism
Tue Nov 29 14:03:33 EST 1994
Block Algorithms and their Derivation





Next:
Examples of Block
Up:
Performance of LAPACK
Previous:
The BLAS as
It is comparatively straightforward to recode many of the algorithms in
LINPACK and EISPACK so that they call Level 2 BLAS
. Indeed, in the simplest
cases the same floating-point operations are performed, possibly even in
the same order: it is just a matter of reorganizing the software. To illustrate
this point we derive the Cholesky factorization algorithm that is used in the
LINPACK
routine SPOFA
, which factorizes a symmetric positive definite matrix
as  . Writing these equations as:
. Writing these equations as:

and equating coefficients of the j-th column, we obtain:

Hence, if

has already been computed, we can compute

and

from the equations:

Here is the body of the code of the LINPACK routine SPOFA
,
which implements the above method:
DO 30 J = 1, N
INFO = J
S = 0.0E0
JM1 = J - 1
IF (JM1 .LT. 1) GO TO 20
DO 10 K = 1, JM1
T = A(K,J) - SDOT(K-1,A(1,K),1,A(1,J),1)
T = T/A(K,K)
A(K,J) = T
S = S + T*T
10 CONTINUE
20 CONTINUE
S = A(J,J) - S
C ......EXIT
IF (S .LE. 0.0E0) GO TO 40
A(J,J) = SQRT(S)
30 CONTINUE
And here is the same computation recoded in ``LAPACK-style''
to use the Level 2 BLAS
routine
STRSV (which solves a triangular system of equations). The call to STRSV
has replaced the loop over K which made several calls to the
Level 1 BLAS routine SDOT. (For reasons given below, this is not the actual
code used in LAPACK - hence the term ``LAPACK-style''.)
DO 10 J = 1, N
CALL STRSV( 'Upper', 'Transpose', 'Non-unit', J-1, A, LDA,
$ A(1,J), 1 )
S = A(J,J) - SDOT( J-1, A(1,J), 1, A(1,J), 1 )
IF( S.LE.ZERO ) GO TO 20
A(J,J) = SQRT( S )
10 CONTINUE
This change by itself is sufficient to make big gains in performance
on a number of machines.
For example, on an IBM RISC Sys/6000-550 (using double precision)
there is virtually no difference in performance between
the LINPACK-style and the LAPACK-style code.
Both styles run at a megaflop rate far below its peak performance for
matrix-matrix multiplication.
To exploit the faster speed of Level 3 BLAS
, the
algorithms must undergo a deeper level of restructuring, and be re-cast as a
block algorithm - that is, an algorithm that operates on blocks
or submatrices of the original matrix.
To derive a block form of Cholesky
factorization
, we write the
defining equation in partitioned form thus:

Equating submatrices in the second block of columns, we obtain:

Hence, if

has already been computed, we can compute

as
the solution to the equation

by a call to the Level 3 BLAS routine STRSM; and then we can compute

from

This involves first updating the symmetric submatrix

by a call to the
Level 3 BLAS routine SSYRK, and then computing its Cholesky factorization.
Since Fortran does not allow recursion, a separate routine must be called
(using Level 2 BLAS rather than Level 3), named SPOTF2 in the code below.
In this way successive blocks of columns of U are computed.
Here is LAPACK-style code for the block algorithm. In this code-fragment
NB denotes the width
of the blocks.
DO 10 J = 1, N, NB
JB = MIN( NB, N-J+1 )
CALL STRSM( 'Left', 'Upper', 'Transpose', 'Non-unit', J-1, JB,
$ ONE, A, LDA, A( 1, J ), LDA )
CALL SSYRK( 'Upper', 'Transpose', JB, J-1, -ONE, A( 1, J ), LDA,
$ ONE, A( J, J ), LDA )
CALL SPOTF2( 'Upper', JB, A( J, J ), LDA, INFO )
IF( INFO.NE.0 ) GO TO 20
10 CONTINUE
But that is not the end of the story, and the code given above is
not the code that is actually used in the LAPACK routine SPOTRF
.
We mentioned in subsection
3.1.1 that for many
linear algebra computations there
are several vectorizable variants, often referred to as i-, j- and
k-variants, according to a convention introduced in
[33]
and used
in
[45]. The same is true of the corresponding block algorithms.
It turns out that the j-variant
that was chosen for LINPACK, and used in the above
examples, is not the fastest on many machines, because it is based on
solving triangular
systems of equations, which can be significantly slower than matrix-matrix
multiplication.
The variant actually used in LAPACK is the i-variant, which does
rely on matrix-matrix multiplication.





Next:
Examples of Block
Up:
Performance of LAPACK
Previous:
The BLAS as
Tue Nov 29 14:03:33 EST 1994
Examples of Block Algorithms in LAPACK





Next:
Factorizations for Solving
Up:
Performance of LAPACK
Previous:
Block Algorithms and
Having discussed in detail the derivation of one particular block algorithm,
we now describe examples of the performance that has been achieved with
a variety of block algorithms. The clock speeds for the
computers involved in the timings are listed in Table
3.2.
-------------------------------------------
Clock Speed
-------------------------------------------
CONVEX C-4640 135 MHz 7.41 ns
CRAY C90 240 MHz 4.167 ns
DEC 3000-500X Alpha 200 MHz 5.0 ns
IBM POWER2 model 590 66 MHz 15.15 ns
IBM RISC Sys/6000-550 42 MHz 23.81 ns
SGI POWER CHALLENGE 75 MHz 13.33 ns
-------------------------------------------
Table 3.2: Clock Speeds of Computers in Timing Results
See Gallivan et al.
[42] and Dongarra et
al.
[31]
for an alternative survey of
algorithms for dense linear
algebra on high-performance computers.
Tue Nov 29 14:03:33 EST 1994
Factorizations for Solving Linear Equations





Next:
Factorization
Up:
Examples of Block
Previous:
Examples of Block
The well-known LU and Cholesky factorizations are the simplest block
algorithms to derive. No extra floating-point operations nor extra
working storage are required.
Table
3.3
illustrates the speed of the LAPACK routine for LU factorization of a
real matrix
,
SGETRF
in single precision on CRAY machines, and DGETRF
in double precision
on all other machines. This corresponds to 64-bit floating-point
arithmetic
on all machines tested. A block size of 1 means that the unblocked algorithm
is used, since it is faster than - or at least as fast as - a
blocked algorithm.
---------------------------------------------------
No. of Block Values of n
processors size 100 1000
---------------------------------------------------
CONVEX C-4640 1 64 274 711
CONVEX C-4640 4 64 379 2588
CRAY C90 1 128 375 863
CRAY C90 16 128 386 7412
DEC 3000-500X Alpha 1 32 53 91
IBM POWER2 model 590 1 32 110 168
IBM RISC Sys/6000-550 1 32 33 56
SGI POWER CHALLENGE 1 64 81 201
SGI POWER CHALLENGE 4 64 79 353
---------------------------------------------------
Table 3.3: Speed in megaflops of SGETRF/DGETRF for square matrices of order n
Table
3.4
gives similar results for Cholesky factorization
.
---------------------------------------------------
No. of Block Values of n
processors size 100 1000
---------------------------------------------------
CONVEX C-4640 1 64 120 546
CONVEX C-4640 4 64 150 1521
CRAY C90 1 128 324 859
CRAY C90 16 128 453 9902
DEC 3000-500X Alpha 1 32 37 83
IBM POWER2 model 590 1 32 102 247
IBM RISC Sys/6000-550 1 32 40 72
SGI POWER CHALLENGE 1 64 74 199
SGI POWER CHALLENGE 4 64 69 424
---------------------------------------------------
Table 3.4: Speed in megaflops of SPOTRF/DPOTRF for matrices of order n with UPLO = `U'
LAPACK, like LINPACK, provides a factorization for symmetric
indefinite
matrices, so that A is factorized as  , where P is a
permutation matrix, and D is block diagonal with blocks of order 1
or 2. A block form of this algorithm has been derived,
and is implemented in the LAPACK routine SSYTRF
/DSYTRF
.
It has to duplicate a little of the computation in order
to ``look ahead''
to determine the necessary row and column interchanges, but the extra work
can be more than compensated for by the greater speed of updating the matrix
by blocks as is illustrated in Table
3.5
.
, where P is a
permutation matrix, and D is block diagonal with blocks of order 1
or 2. A block form of this algorithm has been derived,
and is implemented in the LAPACK routine SSYTRF
/DSYTRF
.
It has to duplicate a little of the computation in order
to ``look ahead''
to determine the necessary row and column interchanges, but the extra work
can be more than compensated for by the greater speed of updating the matrix
by blocks as is illustrated in Table
3.5
.
-------------------
Block Values of n
size 100 1000
-------------------
1 62 86
64 68 165
-------------------
Table 3.5: Speed in megaflops of DSYTRF for matrices of order n with UPLO = `U' on an IBM POWER2 model 590
LAPACK, like LINPACK, provides LU and Cholesky factorizations of
band matrices. The LINPACK algorithms can easily be restructured to use
Level 2 BLAS, though that has little effect on performance for
matrices of very narrow bandwidth. It is also possible to use Level 3 BLAS,
at the price of doing some extra work with zero elements outside the band
[39]. This becomes worthwhile for matrices of large order and
semi-bandwidth greater than 100 or so.





Next:
Factorization
Up:
Examples of Block
Previous:
Examples of Block
Tue Nov 29 14:03:33 EST 1994
<var>QR</var> Factorization





Next:
Eigenvalue Problems
Up:
Examples of Block
Previous:
Factorizations for Solving
The traditional algorithm for QR
factorization
is based on the use of
elementary Householder
matrices of the general form

where v is a column vector and

is a scalar.
This leads to an algorithm with very good vector performance, especially
if coded to use Level 2 BLAS.
The key to developing a block form of this algorithm is to represent a product
of b elementary Householder matrices of order n as a block
form of a Householder matrix
. This can be done in various ways.
LAPACK uses the following form
[68]:

where V is an n-by-n matrix whose columns are the individual vectors

associated with the Householder matrices

, and T is an upper triangular matrix of order b.
Extra work is required to compute the elements of T, but once again this
is compensated for by the greater speed of applying the block form.
Table
3.6
summarizes results obtained with the LAPACK routine SGEQRF
/DGEQRF
.
-------------------------------------------------
No. of Block Values of n
processors size 100 1000
-------------------------------------------------
CONVEX C-4640 1 64 81 521
CONVEX C-4640 4 64 94 1204
CRAY C90 1 128 384 859
CRAY C90 16 128 390 7641
DEC 3000-500X Alpha 1 32 50 86
IBM POWER2 model 590 1 32 108 208
IBM RISC Sys/6000-550 1 32 30 61
SGI POWER CHALLENGE 1 64 61 190
SGI POWER CHALLENGE 4 64 39 342
-------------------------------------------------
Table 3.6: Speed in megaflops of SGEQRF/DGEQRF for square matrices of order n
Tue Nov 29 14:03:33 EST 1994
Eigenvalue Problems





Next:
LAPACK Benchmark
Up:
Examples of Block
Previous:
Factorization
Eigenvalue
problems have until recently
provided a less fertile ground for the
development of block algorithms than the factorizations so far described.
Version 2.0 of LAPACK includes new block algorithms for the symmetric eigenvalue
problem, and future releases will include analogous algorithms for the singular
value decomposition.
The first step in solving many types of eigenvalue problems is to reduce
the original matrix to a ``condensed form'' by orthogonal transformations
.
In the reduction to condensed forms, the unblocked algorithms all use elementary
Householder matrices and have good vector performance.
Block forms of these algorithms have been developed
[34],
but all require additional operations, and a significant proportion of the work
must still be performed by Level 2 BLAS, so there is less possibility of
compensating for the extra operations.
The algorithms concerned are:
- reduction of a symmetric matrix to tridiagonal form
to solve a
symmetric eigenvalue problem: LAPACK routine SSYTRD
applies a symmetric block
update of the form

using the Level 3
BLAS routine SSYR2K; Level 3 BLAS account for at most half the work.
- reduction of a rectangular matrix to bidiagonal form
to compute
a singular value decomposition: LAPACK routine SGEBRD
applies a block update
of the form

using two calls to the
Level 3 BLAS routine SGEMM; Level 3 BLAS account for at most half the
work.
- reduction of a nonsymmetric matrix to Hessenberg form
to solve a
nonsymmetric eigenvalue problem: LAPACK routine SGEHRD
applies a block update
of the form

Level 3 BLAS
account for at most three-quarters of the work.
Note that only in the reduction to Hessenberg form
is it possible to
use the block Householder representation described in
subsection
3.4.2.
Extra work must be performed to compute the n-by-b matrices X and Y
that are required for the block updates (b is the block size)
- and extra workspace is needed to
store them.
Nevertheless, the performance gains can be worthwhile on some machines,
for example, on an IBM POWER2 model 590, as shown in Table
3.7.
(all matrices are square of order n)
----------------------------
Block Values of n
size 100 1000
----------------------------
DSYTRD 1 137 159
16 82 169
----------------------------
DGEBRD 1 90 110
16 90 136
----------------------------
DGEHRD 1 111 113
16 125 187
----------------------------
Table 3.7: Speed in megaflops of reductions to condensed forms on an IBM POWER2 model 590
Following the reduction of a dense (or band) symmetric matrix to tridiagonal form T,
we must compute the eigenvalues and (optionally) eigenvectors of T.
Computing the eigenvalues of T alone (using LAPACK routine SSTERF
) requires
 flops, whereas the reduction routine SSYTRD
does
flops, whereas the reduction routine SSYTRD
does  flops. So eventually the cost of finding eigenvalues
alone becomes small compared to the cost of reduction. However, SSTERF
does only scalar floating point operations, without scope for the BLAS,
so n may have to be large before SSYTRD is slower than SSTERF.
flops. So eventually the cost of finding eigenvalues
alone becomes small compared to the cost of reduction. However, SSTERF
does only scalar floating point operations, without scope for the BLAS,
so n may have to be large before SSYTRD is slower than SSTERF.
Version 2.0 of LAPACK includes a new algorithm, SSTEDC
, for finding all eigenvalues and
eigenvectors of n. The new algorithm can exploit Level 2 and 3 BLAS, whereas
the previous algorithm, SSTEQR
, could not. Furthermore, SSTEDC usually does
many
fewer flops than SSTEQR, so the speedup is compounded. Briefly, SSTEDC works as follows
(for details, see
[67]
[47]). The tridiagonal matrix T is written as

where  and
and  are tridiagonal, and H is a very simple rank-one matrix.
Then the eigenvalues and eigenvectors of
are tridiagonal, and H is a very simple rank-one matrix.
Then the eigenvalues and eigenvectors of  and
and  are found by applying
the algorithm recursively; this yields
are found by applying
the algorithm recursively; this yields  and
and
 , where
, where  is a diagonal matrix of eigenvalues,
and the columns of
is a diagonal matrix of eigenvalues,
and the columns of  are orthonormal eigenvectors. Thus
are orthonormal eigenvectors. Thus

where  is again a simple rank-one matrix. The eigenvalues and eigenvectors
of
is again a simple rank-one matrix. The eigenvalues and eigenvectors
of  may be found
using
may be found
using  scalar operations, yielding
scalar operations, yielding
 Substituting this into the last displayed expression yields
Substituting this into the last displayed expression yields

where the diagonals of  are the desired eigenvalues of T, and the columns
of
are the desired eigenvalues of T, and the columns
of  are the eigenvectors.
Almost all the work is done in the two matrix multiplies of
are the eigenvectors.
Almost all the work is done in the two matrix multiplies of  and
and  times
times
 , which is done using the Level 3 BLAS.
, which is done using the Level 3 BLAS.
The same recursive algorithm can be developed for the singular value decomposition
of the bidiagonal matrix resulting from reducing a dense matrix with SGEBRD.
This software will be completed for a future release of LAPACK.
The current LAPACK algorithm for the bidiagonal singular values
decomposition, SBDSQR
, does not use the Level 2 or Level 3 BLAS.
For computing the eigenvalues and eigenvectors of a Hessenberg
matrix-or rather for computing its Schur factorization- yet another
flavour of block algorithm has been developed: a multishift
QR iteration
[8]. Whereas the traditional EISPACK routine
HQR
uses a double shift (and the corresponding complex
routine COMQR
uses a single shift), the multishift algorithm uses block shifts of
higher order. It has been found that often the total number of operations
decreases as the order of shift is increased until a minimum
is reached typically between 4 and 8; for higher orders the number of
operations increases quite rapidly. On many machines
the speed of applying the shift
increases steadily with the order, and the optimum order of shift is
typically in the range 8-16. Note however that the performance can be
very sensitive to the choice of the order of shift; it also depends on
the numerical properties of the matrix. Dubrulle
[37] has
studied the practical performance of the algorithm, while Watkins and
Elsner
[77] discuss its theoretical asymptotic convergence
rate.
Finally, we note that research into block algorithms for symmetric and
nonsymmetric eigenproblems continues
[55]
[9],
and future versions of LAPACK will be updated to contain the best algorithms available.





Next:
LAPACK Benchmark
Up:
Examples of Block
Previous:
Factorization
Tue Nov 29 14:03:33 EST 1994
LAPACK





Next:
Problems that LAPACK
Up:
Essentials
Previous:
Essentials
LAPACK is a library of Fortran 77 subroutines for solving
the most commonly
occurring problems in numerical linear algebra.
It has been designed to be efficient on a wide range of modern
high-performance computers. The name LAPACK is an acronym for Linear
Algebra PACKage.
Tue Nov 29 14:03:33 EST 1994
LAPACK Benchmark





Next:
Accuracy and Stability
Up:
Performance of LAPACK
Previous:
Eigenvalue Problems
This section contains performance numbers for selected LAPACK driver routines.
These routines provide complete solutions for the most common problems of numerical
linear algebra, and are the routines users are most likely to call:
- Solve an n-by-n system of linear equations with 1 right hand side
using SGESV/DGESV.
- Solve an n-by-n linear least squares problem with 1 right hand side
using SGELS/DGELS.
- Find only the eigenvalues of an n-by-n nonsymmetric matrix using SGEEV/DGEEV.
- Find the eigenvalues and right eigenvectors of an n-by-n nonsymmetric matrix using
SGEEV/DGEEV.
- Find only the eigenvalues of an n-by-n symmetric matrix using
SSYEVD/DSYEVD.
- Find the eigenvalues and eigenvectors of an n-by-n symmetric matrix using
SSYEVD/DSYEVD.
- Find only the singular values of an n-by-n matrix using SGESVD/DGESVD.
- Find the singular values and right and left singular vectors of an
n-by-n matrix using
SGESVD/DGESVD.
Data is provided for a variety of vector computers, shared memory parallel
computers, and high performance workstations. All timings were obtained by
using the machine-specific optimized BLAS available on each machine. For
the IBM RISC Sys/6000-550 and IBM POWER2 model 590, the ESSL BLAS were used.
In all cases the data consisted
of 64-bit floating point numbers (single precision on the CRAY C90 and
double precision on the other machines).
For each machine and each driver, a small problem
(N = 100 with LDA = 101) and a large problem (N = 1000 with LDA = 1001) were
run. Block sizes NB = 1, 16, 32 and 64 were
tried, with data only for the fastest run reported in the tables below.
Similarly, UPLO = 'L' and UPLO = 'U' were timed for SSYEVD/DSYEVD, but only
times for UPLO = 'U' were reported. For SGEEV/DGEEV, ILO = 1 and
IHI = N. The test matrices were generated with randomly distributed entries.
All run times are reported in seconds, and block size is denoted by
nb. The value of nb was chosen to make N = 1000 optimal. It is not
necessarily the best choice for N = 100. See Section
6.2
for details.
The performance data is reported using three or four statistics. First, the
run-time in seconds is given. The second statistic measures
how well our performance compares to the speed of the BLAS, specifically
SGEMM/DGEMM. This ``equivalent matrix multiplies'' statistic is calculated as

and labeled as  in the tables.
The performance information for the BLAS routines
in the tables.
The performance information for the BLAS routines
SGEMV/DGEMV (TRANS='N')
and SGEMM/DGEMM (TRANSA='N', TRANSB='N') is provided in Table
3.8,
along with the clock speed for each machine in Table
3.2.
The third statistic is the true megaflop rating. For
the eigenvalue and singular value drivers, a fourth ``synthetic megaflop''
statistic is also presented. We provide this statistic because the number
of floating point operations needed to find eigenvalues and singular values
depends on the input data, unlike linear equation solving or linear least
squares solving with SGELS/DGELS. The synthetic megaflop rating is defined
to be the ``standard'' number of flops required to solve the problem, divided
by the run-time in microseconds. This ``standard'' number of flops is taken
to be the average for a standard algorithm over a variety of problems, as
given in Table
3.9
(we ignore terms of order  )
[45].
)
[45].

Table 3.8: Execution time and Megaflop rates for SGEMV/DGEMV and
SGEMM/DGEMM
Note that the synthetic megaflop rating is much higher than the true megaflop
rating for
SSYEVD/DSYEVD in Table
3.15; this is because SSYEVD/DSYEVD
performs many fewer floating point operations than the standard algorithm, SSYEV/DSYEV.

Table 3.9: ``Standard'' floating point operation counts for LAPACK drivers
for n-by-n matrices

Table 3.10: Performance of SGESV/DGESV for n-by-n matrices

Table 3.11: Performance of SGELS/DGELS for n-by-n matrices

Table 3.12: Performance of SGEEV/DGEEV, eigenvalues only

Table 3.13: Performance of SGEEV/DGEEV, eigenvalues and right eigenvectors

Table 3.14: Performance of SSYEVD/DSYEVD, eigenvalues only, UPLO='U'

Table 3.15: Performance of SSYEVD/DSYEVD, eigenvalues and eigenvectors, UPLO='U'

Table 3.16: Performance of SGESVD/DGESVD, singular values only

Table 3.17: Performance of SGESVD/DGESVD, singular values and left and right singular vectors





Next:
Accuracy and Stability
Up:
Performance of LAPACK
Previous:
Eigenvalue Problems
Tue Nov 29 14:03:33 EST 1994
Accuracy and Stability





Next:
Sources of Error
Up:
Guide
Previous:
LAPACK Benchmark
In addition to providing faster routines than previously available,
LAPACK provides more comprehensive and better
error
bounds
.
Our ultimate goal is to provide error bounds for all
quantities computed by LAPACK.
In this chapter we explain our overall approach to obtaining error bounds,
and provide enough information to use the software.
The comments at the beginning of the individual routines should be consulted
for more details.
It is beyond the scope of this chapter to justify all the bounds
we present. Instead, we give references to the literature.
For example, standard material on error analysis can be found
in
[45].
In order to make this chapter easy to read, we have labeled sections
not essential for a first reading as Further Details. The sections
not labeled as Further Details should provide all the information
needed to understand and use the main error bounds computed by
LAPACK. The Further Details sections provide mathematical background,
references, and tighter but more expensive error bounds, and may be read later.
In section
4.1
we discuss the sources of numerical error, in particular roundoff
error.
Section
4.2 discusses how to measure errors,
as well as some standard notation.
Section
4.3 discusses further details
of how error bounds are derived.
Sections
4.4 through
4.12 present error bounds
for linear equations, linear least squares problems,
generalized linear least squares problems,
the symmetric eigenproblem,
the nonsymmetric eigenproblem,
the singular value decomposition,
the generalized symmetric definite eigenproblem,
the generalized nonsymmetric eigenproblem
and the
generalized (or quotient) singular value decomposition respectively.
Section
4.13 discusses the impact of fast
Level 3 BLAS
on
the accuracy
of LAPACK routines.
The sections on
generalized linear least squares problems and
the generalized nonsymmetric eigenproblem are
``placeholders'' to be
completed in the next versions of the library and manual.
The next versions will also include
error bounds for new high accuracy
routines for the symmetric
eigenvalue problem and singular value decomposition.





Next:
Sources of Error
Up:
Guide
Previous:
LAPACK Benchmark
Tue Nov 29 14:03:33 EST 1994
Sources of Error in Numerical Calculations





Next:
Further Details: Floating
Up:
Accuracy and Stability
Previous:
Accuracy and Stability
There are two sources of error whose effects can be measured by the bounds in
this chapter: roundoff error and input error. Roundoff error
arises from rounding results of floating-point operations during
the algorithm.
Input error is error in the input to the algorithm from prior calculations or
measurements. We describe roundoff error first, and then input error.
Almost all the error bounds LAPACK provides are multiples of
machine epsilon,
which we abbreviate
by  . Machine epsilon bounds the roundoff in individual
floating-point operations.
It may be loosely defined as the largest relative error
in any floating-point operation that neither overflows nor underflows.
(Overflow means the result is too
large to represent accurately, and underflow means the result is too
small to represent accurately.) Machine epsilon is available either by
the function call
SLAMCH('Epsilon') (or simply SLAMCH('E')) in single precision, or
by the function call DLAMCH('Epsilon') (or DLAMCH('E')) in double precision.
See section
4.1.1 and
Table
4.1 for a discussion of common values of machine
epsilon.
. Machine epsilon bounds the roundoff in individual
floating-point operations.
It may be loosely defined as the largest relative error
in any floating-point operation that neither overflows nor underflows.
(Overflow means the result is too
large to represent accurately, and underflow means the result is too
small to represent accurately.) Machine epsilon is available either by
the function call
SLAMCH('Epsilon') (or simply SLAMCH('E')) in single precision, or
by the function call DLAMCH('Epsilon') (or DLAMCH('E')) in double precision.
See section
4.1.1 and
Table
4.1 for a discussion of common values of machine
epsilon.
Since overflow generally causes an error message, and
underflow is almost always less significant than roundoff, we will not
consider overflow and underflow further
(see section
4.1.1).
Bounds on input errors, or errors in the input parameters inherited
from prior computations or measurements, may be easily incorporated
into most LAPACK error bounds.
Suppose the input data is accurate to, say, 5 decimal digits
(we discuss exactly what
this means in section
4.2). Then one simply replaces
 by
by  in the error bounds.
in the error bounds.
Tue Nov 29 14:03:33 EST 1994
Further Details: Floating point arithmetic





Next:
How to Measure
Up:
Sources of Error
Previous:
Sources of Error
Roundoff error is bounded in terms of the machine precision
 ,
which is the smallest value satisfying
,
which is the smallest value satisfying

where  and
and  are floating-point numbers
,
are floating-point numbers
,
 is any one of the four operations +,
is any one of the four operations +,  ,
,  and
and  ,
and
,
and  is the floating-point result of
is the floating-point result of  .
Machine epsilon,
.
Machine epsilon,  , is the smallest value for which this inequality
is true for all
, is the smallest value for which this inequality
is true for all  , and for all
, and for all  and
and  such that
such that
 is neither too large (magnitude exceeds the overflow
threshold)
nor too small
(is nonzero with magnitude less than the underflow threshold)
to be represented accurately in the machine.
We also assume
is neither too large (magnitude exceeds the overflow
threshold)
nor too small
(is nonzero with magnitude less than the underflow threshold)
to be represented accurately in the machine.
We also assume  bounds the relative error in unary
operations like square root:
bounds the relative error in unary
operations like square root:

A precise characterization of  depends on the details of the
machine arithmetic and sometimes even of the compiler.
For example, if addition and
subtraction are implemented without a guard digit
depends on the details of the
machine arithmetic and sometimes even of the compiler.
For example, if addition and
subtraction are implemented without a guard digit
 we must redefine
we must redefine  to be the smallest number
such that
to be the smallest number
such that

In order to assure portability
,
machine parameters such as machine epsilon, the overflow threshold and
underflow threshold are computed at runtime by the auxiliary
routine xLAMCH
 . The alternative,
keeping a fixed table of machine parameter values, would degrade portability
because the table would have to be changed when moving from one machine,
or even one compiler, to another.
. The alternative,
keeping a fixed table of machine parameter values, would degrade portability
because the table would have to be changed when moving from one machine,
or even one compiler, to another.
Actually, most machines, but not yet all, do have the same machine
parameters because they implement IEEE Standard Floating Point Arithmetic
[5]
[4], which exactly specifies floating-point number
representations and operations. For
these machines, including all modern workstations and
PCs
 ,
the values of these parameters are given in
Table
4.1.
,
the values of these parameters are given in
Table
4.1.

Table 4.1: Values of Machine Parameters in IEEE Floating Point Arithmetic
As stated above, we will ignore overflow and underflow in discussing error
bounds. Reference
[18] discusses extending error bounds
to include
underflow, and shows that for many common computations, when underflow occurs it
is less significant than roundoff. Overflow generally causes an error
message and stops execution, so the error bounds do not
apply
 .
.
Therefore, most of our error bounds will simply be proportional to machine epsilon.
This means, for example, that if the
same problem in solved in double precision and single precision, the error bound
in double precision will be smaller than the error bound in single precision
by a factor
of  . In IEEE arithmetic, this
ratio is
. In IEEE arithmetic, this
ratio is  ,
meaning that one expects the double precision answer to have approximately nine
more decimal digits correct than the single precision answer.
,
meaning that one expects the double precision answer to have approximately nine
more decimal digits correct than the single precision answer.
LAPACK routines are generally insensitive to the details of rounding, like
their counterparts in LINPACK and EISPACK. One newer
algorithm (xLASV2) can return significantly more accurate results if
addition and subtraction have a guard digit
(see the end of section
4.9).





Next:
How to Measure
Up:
Sources of Error
Previous:
Sources of Error
Tue Nov 29 14:03:33 EST 1994
How to Measure Errors





Next:
Further Details: How
Up:
Accuracy and Stability
Previous:
Further Details: Floating
LAPACK routines return four types of floating-point output arguments:
- Scalar, such as an eigenvalue of a matrix,
- Vector, such as the solution x of a linear system Ax = b,
- Matrix, such as a matrix inverse
 , and
, and
- Subspace, such as the space spanned by one or more eigenvectors of a matrix.
This section provides measures for errors in these quantities, which we
need in order to express error bounds.
First consider scalars. Let the scalar  be an approximation of
the true answer
be an approximation of
the true answer  . We can measure the difference between
. We can measure the difference between  and
and  either by the absolute error
either by the absolute error
 , or, if
, or, if  is nonzero, by the relative error
is nonzero, by the relative error
 . Alternatively, it is sometimes more convenient
to use
. Alternatively, it is sometimes more convenient
to use  instead of the standard expression
for relative error (see section
4.2.1).
If the relative error of
instead of the standard expression
for relative error (see section
4.2.1).
If the relative error of  is, say
is, say  , then we say that
, then we say that
 is accurate to 5 decimal digits.
is accurate to 5 decimal digits.
In order to measure the error in vectors, we need to measure the size
or norm of a vector x
. A popular norm
is the magnitude of the largest component,  , which we denote
, which we denote
 . This is read the infinity norm of x.
See Table
4.2 for a summary of norms.
. This is read the infinity norm of x.
See Table
4.2 for a summary of norms.

Table 4.2: Vector and matrix norms
If  is an approximation to the
exact vector x, we will refer to
is an approximation to the
exact vector x, we will refer to  as the
absolute error in
as the
absolute error in  (where p is one of the values in Table
4.2),
and refer to
(where p is one of the values in Table
4.2),
and refer to  as the relative error
in
as the relative error
in  (assuming
(assuming  ). As with scalars,
we will sometimes use
). As with scalars,
we will sometimes use  for the relative error.
As above, if the relative error of
for the relative error.
As above, if the relative error of  is, say
is, say  , then we say
that
, then we say
that  is accurate to 5 decimal digits.
The following example illustrates these ideas:
is accurate to 5 decimal digits.
The following example illustrates these ideas:


Thus, we would say that  approximates x to 2
decimal digits.
approximates x to 2
decimal digits.
Errors in matrices may also be measured with norms
.
The most obvious
generalization of  to matrices would appear to be
to matrices would appear to be
 , but this does not have certain
important mathematical properties that make deriving error bounds
convenient (see section
4.2.1).
Instead, we will use
, but this does not have certain
important mathematical properties that make deriving error bounds
convenient (see section
4.2.1).
Instead, we will use
 ,
where A is an m-by-n matrix, or
,
where A is an m-by-n matrix, or
 ;
see Table
4.2 for other matrix norms.
As before
;
see Table
4.2 for other matrix norms.
As before  is the absolute
error
in
is the absolute
error
in  ,
,  is the relative error
in
is the relative error
in  , and a relative error in
, and a relative error in  of
of
 means
means  is accurate to 5 decimal digits.
The following example illustrates these ideas:
is accurate to 5 decimal digits.
The following example illustrates these ideas:


so  is accurate to 1 decimal digit.
is accurate to 1 decimal digit.
Here is some related notation we will use in our error bounds.
The condition number of a matrix A is defined as
 , where A
is square and invertible, and p is
, where A
is square and invertible, and p is  or one of the other
possibilities in Table
4.2. The condition number
measures how sensitive
or one of the other
possibilities in Table
4.2. The condition number
measures how sensitive  is to changes in A; the larger
the condition number, the more sensitive is
is to changes in A; the larger
the condition number, the more sensitive is  . For example,
for the same A as in the last example,
. For example,
for the same A as in the last example,

LAPACK
error estimation routines typically compute a variable called
RCOND
, which is the reciprocal of the condition number (or an
approximation of the reciprocal). The reciprocal of the condition
number is used instead of the condition number itself in order
to avoid the possibility of overflow when the condition number is very large.
Also, some of our error bounds will use the vector of absolute values
of x,  (
( ), or similarly
), or similarly  (
( ).
).
Now we consider errors in subspaces. Subspaces are the
outputs of routines that compute eigenvectors and invariant
subspaces of matrices. We need a careful definition
of error in these cases for the following reason. The nonzero vector x is called a
(right) eigenvector of the matrix A with eigenvalue
 if
if  . From this definition, we see that
-x, 2x, or any other nonzero multiple
. From this definition, we see that
-x, 2x, or any other nonzero multiple  of x is also an
eigenvector. In other words, eigenvectors are not unique. This
means we cannot measure the difference between two supposed eigenvectors
of x is also an
eigenvector. In other words, eigenvectors are not unique. This
means we cannot measure the difference between two supposed eigenvectors
 and x by computing
and x by computing  , because this may
be large while
, because this may
be large while  is small or even zero for
some
is small or even zero for
some  . This is true
even if we normalize n so that
. This is true
even if we normalize n so that  , since both
x and -x can be normalized simultaneously. So in order to define
error in a useful way, we need to instead consider the set S of
all scalar multiples
, since both
x and -x can be normalized simultaneously. So in order to define
error in a useful way, we need to instead consider the set S of
all scalar multiples  of
x. The set S is
called the subspace spanned by x, and is uniquely determined
by any nonzero member of S. We will measure the difference
between two such sets by the acute angle between them.
Suppose
of
x. The set S is
called the subspace spanned by x, and is uniquely determined
by any nonzero member of S. We will measure the difference
between two such sets by the acute angle between them.
Suppose  is spanned by
is spanned by  and
S is spanned by {x}. Then the acute angle between
and
S is spanned by {x}. Then the acute angle between
 and S is defined as
and S is defined as

One can show that  does not change when either
does not change when either
 or x is multiplied by any nonzero scalar. For example, if
or x is multiplied by any nonzero scalar. For example, if

as above, then  for any
nonzero scalars
for any
nonzero scalars  and
and  .
.
Here is another way to interpret the angle  between
between  and
S.
Suppose
and
S.
Suppose  is a unit vector (
is a unit vector ( ).
Then there is a scalar
).
Then there is a scalar  such that
such that

The approximation  holds when
holds when  is much less than 1
(less than .1 will do nicely). If
is much less than 1
(less than .1 will do nicely). If  is an approximate
eigenvector with error bound
is an approximate
eigenvector with error bound  ,
where x is a true eigenvector, there is another true eigenvector
,
where x is a true eigenvector, there is another true eigenvector
 satisfying
satisfying  .
For example, if
.
For example, if

then  for
for  .
.
Some LAPACK routines also return subspaces spanned by more than one
vector, such as the invariant subspaces of matrices returned by xGEESX.
The notion of angle between subspaces also applies here;
see section
4.2.1 for details.
Finally, many of our error bounds will contain a factor p(n) (or p(m , n)),
which grows as a function of matrix dimension n (or dimensions m and n).
It represents a potentially different function for each problem.
In practice, the true errors usually grow just linearly; using
p(n) = 10n in the error bound formulas will often give a reasonable bound.
Therefore, we will refer to p(n) as a ``modestly growing'' function of n.
However it can occasionally be much larger, see
section
4.2.1.
For simplicity, the error bounds computed by the code fragments
in the following sections will use p(n) = 1.
This means these computed error bounds may occasionally
slightly underestimate the true error. For this reason we refer
to these computed error bounds as ``approximate error bounds''.





Next:
Further Details: How
Up:
Accuracy and Stability
Previous:
Further Details: Floating
Tue Nov 29 14:03:33 EST 1994
Further Details: How to Measure Errors





Next:
Further Details: How
Up:
How to Measure
Previous:
How to Measure
The relative error  in the approximation
in the approximation
 of the true solution
of the true solution  has a drawback: it often cannot
be computed directly, because it depends on the unknown quantity
has a drawback: it often cannot
be computed directly, because it depends on the unknown quantity
 . However, we can often instead estimate
. However, we can often instead estimate
 , since
, since  is
known (it is the output of our algorithm). Fortunately, these two
quantities are necessarily close together, provided either one is small,
which is the only time they provide a useful bound anyway. For example,
is
known (it is the output of our algorithm). Fortunately, these two
quantities are necessarily close together, provided either one is small,
which is the only time they provide a useful bound anyway. For example,
 implies
implies

so they can be used interchangeably.
Table
4.2 contains a variety of norms we will use to
measure errors.
These norms have the properties that
 , and
, and
 , where p is one of
1, 2,
, where p is one of
1, 2,  , and F. These properties are useful for deriving
error bounds.
, and F. These properties are useful for deriving
error bounds.
An error bound that uses a given norm may be changed into an error bound
that uses another norm. This is accomplished by multiplying the first
error bound by an appropriate function of the problem dimension.
Table
4.3 gives the
factors  such that
such that  , where
n is the dimension of x.
, where
n is the dimension of x.

Table 4.3: Bounding One Vector Norm in Terms of Another
Table
4.4 gives the
factors  such that
such that  , where
A is m-by-n.
, where
A is m-by-n.

Table 4.4: Bounding One Matrix Norm in Terms of Another
The two-norm of A,  , is also called the spectral
norm of A, and is equal to the largest singular value
, is also called the spectral
norm of A, and is equal to the largest singular value
 of A.
We shall also need to refer to the smallest singular value
of A.
We shall also need to refer to the smallest singular value
 of A; its value can be defined in a similar way to
the definition of the two-norm in Table
4.2, namely as
of A; its value can be defined in a similar way to
the definition of the two-norm in Table
4.2, namely as
 when A
has at least as many rows as columns, and defined as
when A
has at least as many rows as columns, and defined as
 when A has more
columns than rows. The two-norm,
Frobenius norm
,
and singular values of a matrix do not change
if the matrix is multiplied by a real orthogonal (or complex unitary) matrix.
when A has more
columns than rows. The two-norm,
Frobenius norm
,
and singular values of a matrix do not change
if the matrix is multiplied by a real orthogonal (or complex unitary) matrix.
Now we define subspaces spanned by more than one vector,
and angles between subspaces.
Given a set of k
n-dimensional vectors  , they determine
a subspace S consisting of all their possible linear combinations
, they determine
a subspace S consisting of all their possible linear combinations
 ,
,  scalars
scalars  . We also
say that
. We also
say that  spans S.
The difficulty in measuring the difference between subspaces is that
the sets of vectors spanning them are not unique.
For example, {x}, {-x} and {2x} all determine the
same subspace.
This means we cannot simply compare the subspaces spanned by
spans S.
The difficulty in measuring the difference between subspaces is that
the sets of vectors spanning them are not unique.
For example, {x}, {-x} and {2x} all determine the
same subspace.
This means we cannot simply compare the subspaces spanned by
 and
and  by
comparing each
by
comparing each  to
to  . Instead, we will measure the angle
between the subspaces, which is independent of the spanning set
of vectors. Suppose subspace
. Instead, we will measure the angle
between the subspaces, which is independent of the spanning set
of vectors. Suppose subspace  is spanned by
is spanned by
 and that subspace S
is spanned by
and that subspace S
is spanned by  . If k = 1, we instead write more
simply
. If k = 1, we instead write more
simply  and {x}.
When k = 1, we defined
the angle
and {x}.
When k = 1, we defined
the angle  between
between
 and S as the acute angle
between
and S as the acute angle
between  and
and  .
When k > 1, we define the acute angle between
.
When k > 1, we define the acute angle between  and
S as the largest acute angle between any vector
and
S as the largest acute angle between any vector  in
in
 , and the closest vector x in S to
, and the closest vector x in S to  :
:

LAPACK routines which compute subspaces return
vectors  spanning a subspace
spanning a subspace
 which are orthonormal. This means the
n-by-k matrix
which are orthonormal. This means the
n-by-k matrix  satisfies
satisfies  . Suppose also that
the vectors
. Suppose also that
the vectors  spanning S
are orthonormal, so
spanning S
are orthonormal, so  also
satisfies
also
satisfies  .
Then there is a simple expression for the angle between
.
Then there is a simple expression for the angle between
 and S:
and S:

For example, if

then  .
.
As stated above, all our bounds will contain a factor
p(n) (or p(m,n)), which measure how roundoff errors can grow
as a function of matrix dimension n (or m and n).
In practice, the true error usually grows just linearly with n,
but we can generally only prove much weaker bounds of the form  .
This is because we can not rule out the extremely unlikely possibility of rounding
errors all adding together instead of canceling on average. Using
.
This is because we can not rule out the extremely unlikely possibility of rounding
errors all adding together instead of canceling on average. Using
 would give very pessimistic and unrealistic bounds, especially
for large n, so we content ourselves with describing p(n) as a
``modestly growing'' polynomial function of n. Using p(n) = 10n in
the error bound formulas will often give a reasonable bound.
For detailed derivations of various
p(n), see
[78]
[45].
would give very pessimistic and unrealistic bounds, especially
for large n, so we content ourselves with describing p(n) as a
``modestly growing'' polynomial function of n. Using p(n) = 10n in
the error bound formulas will often give a reasonable bound.
For detailed derivations of various
p(n), see
[78]
[45].
There is also one situation where p(n) can grow as large as  :
Gaussian elimination. This typically occurs only on specially constructed
matrices presented in numerical analysis courses [p. 212]wilkinson1.
However, the expert drivers for solving linear systems, xGESVX and xGBSVX,
provide error bounds incorporating p(n), and so this rare possibility
can be detected.
:
Gaussian elimination. This typically occurs only on specially constructed
matrices presented in numerical analysis courses [p. 212]wilkinson1.
However, the expert drivers for solving linear systems, xGESVX and xGBSVX,
provide error bounds incorporating p(n), and so this rare possibility
can be detected.





Next:
Further Details: How
Up:
How to Measure
Previous:
How to Measure
Tue Nov 29 14:03:33 EST 1994
Further Details: How Error Bounds Are Derived





Next:
Standard Error Analysis
Up:
Accuracy and Stability
Previous:
Further Details: How
Tue Nov 29 14:03:33 EST 1994
Standard Error Analysis





Next:
Improved Error Bounds
Up:
Further Details: How
Previous:
Further Details: How
We illustrate standard error analysis with the simple example of
evaluating the scalar function y = f(z). Let the output of the
subroutine which implements f(z) be denoted alg(z); this includes
the effects of roundoff. If  where
where  is small,
then we say alg is a backward stable
algorithm for f,
or that the backward error
is small,
then we say alg is a backward stable
algorithm for f,
or that the backward error  is small.
In other words, alg(z) is the
exact value of f at a slightly perturbed input
is small.
In other words, alg(z) is the
exact value of f at a slightly perturbed input  .
.

Suppose now that f is a smooth function, so that
we may approximate it near z by a straight line:
 .
Then we have the simple error estimate
.
Then we have the simple error estimate

Thus, if  is small, and the derivative
is small, and the derivative  is
moderate, the error alg(z) - f(z) will be small
is
moderate, the error alg(z) - f(z) will be small
 .
This is often written
in the similar form
.
This is often written
in the similar form

This approximately bounds the relative error
 by the product of
the condition number of
f at z,
by the product of
the condition number of
f at z,  , and the
relative backward error
, and the
relative backward error  .
Thus we get an error bound by multiplying a
condition
number and
a backward error (or bounds for these quantities). We call a problem
ill-conditioned
if its condition number is large,
and ill-posed
if its condition number is infinite (or does not exist)
.
Thus we get an error bound by multiplying a
condition
number and
a backward error (or bounds for these quantities). We call a problem
ill-conditioned
if its condition number is large,
and ill-posed
if its condition number is infinite (or does not exist)
 .
.
If f and z are vector quantities, then  is a matrix
(the Jacobian). So instead of using absolute values as before,
we now measure
is a matrix
(the Jacobian). So instead of using absolute values as before,
we now measure  by a vector norm
by a vector norm  and
and  by a matrix norm
by a matrix norm  . The conventional (and coarsest) error analysis
uses a norm such as the infinity norm. We therefore call
this normwise backward stability.
For example, a normwise stable
method for solving a system of linear equations Ax = b will
produce a solution
. The conventional (and coarsest) error analysis
uses a norm such as the infinity norm. We therefore call
this normwise backward stability.
For example, a normwise stable
method for solving a system of linear equations Ax = b will
produce a solution  satisfying
satisfying  where
where
 and
and
 are both small (close to machine epsilon).
In this case the condition number is
are both small (close to machine epsilon).
In this case the condition number is
 (see section
4.4 below).
(see section
4.4 below).
Almost all of the algorithms in LAPACK (as well as LINPACK and EISPACK)
are stable in the sense just described
 :
when applied to a matrix A
they produce the exact result for a slightly different matrix A + E,
where
:
when applied to a matrix A
they produce the exact result for a slightly different matrix A + E,
where  is of order
is of order  .
.
Condition numbers may be expensive to compute
exactly.
For example, it costs about  operations to solve Ax = b
for a general matrix A, and computing
operations to solve Ax = b
for a general matrix A, and computing  exactly costs
an additional
exactly costs
an additional  operations, or twice as much.
But
operations, or twice as much.
But  can be estimated in only
can be estimated in only  operations beyond those
operations beyond those  necessary for solution,
a tiny extra cost. Therefore, most of LAPACK's condition numbers
and error bounds are based on estimated condition
numbers
, using the method
of
[52]
[51]
[48].
The price one pays for using an estimated rather than an
exact condition number is occasional
(but very rare) underestimates of the true error; years of experience
attest to the reliability of our estimators, although examples
where they badly underestimate the error can be constructed
[53].
Note that once a condition estimate is large enough,
(usually
necessary for solution,
a tiny extra cost. Therefore, most of LAPACK's condition numbers
and error bounds are based on estimated condition
numbers
, using the method
of
[52]
[51]
[48].
The price one pays for using an estimated rather than an
exact condition number is occasional
(but very rare) underestimates of the true error; years of experience
attest to the reliability of our estimators, although examples
where they badly underestimate the error can be constructed
[53].
Note that once a condition estimate is large enough,
(usually  ), it confirms that the computed
answer may be completely inaccurate, and so the exact magnitude
of the condition estimate conveys little information.
), it confirms that the computed
answer may be completely inaccurate, and so the exact magnitude
of the condition estimate conveys little information.





Next:
Improved Error Bounds
Up:
Further Details: How
Previous:
Further Details: How
Tue Nov 29 14:03:33 EST 1994
Improved Error Bounds





Next:
Error Bounds for
Up:
Further Details: How
Previous:
Standard Error Analysis
The standard error analysis just outlined has a drawback: by using the
infinity norm  to measure the backward error,
entries of equal magnitude in
to measure the backward error,
entries of equal magnitude in  contribute equally to the final
error bound
contribute equally to the final
error bound  . This means that
if z is sparse or has some very tiny entries, a normwise backward
stable algorithm may make very large changes in these entries
compared to their original values. If these tiny values are known accurately
by the user, these errors may be unacceptable,
or the error bounds may be unacceptably large.
. This means that
if z is sparse or has some very tiny entries, a normwise backward
stable algorithm may make very large changes in these entries
compared to their original values. If these tiny values are known accurately
by the user, these errors may be unacceptable,
or the error bounds may be unacceptably large.
For example, consider solving a diagonal system of linear equations Ax = b.
Each component of the solution is computed accurately by
Gaussian elimination:  .
The usual error bound is approximately
.
The usual error bound is approximately
 ,
which can arbitrarily overestimate the true error,
,
which can arbitrarily overestimate the true error,  , if at least one
, if at least one
 is tiny and another one is large.
is tiny and another one is large.
LAPACK addresses this inadequacy by providing some algorithms
whose backward error  is a tiny relative change in
each component of z:
is a tiny relative change in
each component of z:  .
This backward error retains both the sparsity structure of z as
well as the information in tiny entries. These algorithms are therefore
called componentwise relatively backward stable.
Furthermore, computed error bounds reflect this stronger form of backward
error
.
This backward error retains both the sparsity structure of z as
well as the information in tiny entries. These algorithms are therefore
called componentwise relatively backward stable.
Furthermore, computed error bounds reflect this stronger form of backward
error
 .
.
If the input data has independent uncertainty in each component,
each component must have at least a small relative uncertainty,
since each is a floating-point number.
In this case, the extra uncertainty contributed by the algorithm is not much
worse than the uncertainty in the input data, so
one could say the answer provided by a componentwise
relatively backward stable algorithm is as accurate as the data
warrants
[1].
When solving Ax = b using expert driver xyySVX or computational routine xyyRFS,
for example, we almost always
compute  satisfying
satisfying  , where
, where
 is a small relative change in
is a small relative change in  and
and
 is a small relative change in
is a small relative change in  . In particular, if A is diagonal,
the corresponding error bound is always tiny, as one would
expect (see the next section).
. In particular, if A is diagonal,
the corresponding error bound is always tiny, as one would
expect (see the next section).
LAPACK can achieve this accuracy
for linear equation solving,
the bidiagonal singular value decomposition, and
the symmetric tridiagonal eigenproblem,
and provides facilities for achieving this accuracy for least squares problems.
Future versions of LAPACK will also achieve this
accuracy for other linear algebra problems, as discussed below.





Next:
Error Bounds for
Up:
Further Details: How
Previous:
Standard Error Analysis
Tue Nov 29 14:03:33 EST 1994
Error Bounds for Linear Equation Solving





Next:
Further Details: Error
Up:
Accuracy and Stability
Previous:
Improved Error Bounds
Let Ax = b be the system to be solved, and  the computed
solution. Let n be the dimension of A.
An approximate error bound
for
the computed
solution. Let n be the dimension of A.
An approximate error bound
for  may be obtained in one of the following two ways,
depending on whether the solution is computed by a simple driver or
an expert driver:
may be obtained in one of the following two ways,
depending on whether the solution is computed by a simple driver or
an expert driver:
- Suppose that Ax = b is solved using the simple driver SGESV
(subsection
2.2.1).
Then the approximate error bound


can be computed by the following code fragment.
EPSMCH = SLAMCH( 'E' )
* Get infinity-norm of A
ANORM = SLANGE( 'I', N, N, A, LDA, WORK )
* Solve system; The solution X overwrites B
CALL SGESV( N, 1, A, LDA, IPIV, B, LDB, INFO )
IF( INFO.GT.0 ) THEN
PRINT *,'Singular Matrix'
ELSE IF (N .GT. 0) THEN
* Get reciprocal condition number RCOND of A
CALL SGECON( 'I', N, A, LDA, ANORM, RCOND,
$ WORK, IWORK, INFO )
RCOND = MAX( RCOND, EPSMCH )
ERRBD = EPSMCH / RCOND
END IF
For example, suppose

 ,
,

Then (to 4 decimal places)

 ,
,
 ,
the true reciprocal condition number
,
the true reciprocal condition number  ,
,
 , and the true error
, and the true error
 .
.
- Suppose that Ax = b is solved using the expert driver SGESVX
(subsection
2.2.1).
This routine provides an explicit error bound FERR, measured
with the infinity-norm:

For example, the following code fragment solves
Ax = b and computes an approximate error bound FERR:
CALL SGESVX( 'E', 'N', N, 1, A, LDA, AF, LDAF, IPIV,
$ EQUED, R, C, B, LDB, X, LDX, RCOND, FERR, BERR,
$ WORK, IWORK, INFO )
IF( INFO.GT.0 ) PRINT *,'(Nearly) Singular Matrix'
For the same A and b as above,
 ,
,
 ,
and the actual error is
,
and the actual error is  .
.
This example illustrates
that the expert driver provides an error bound with less programming
effort than the simple driver, and also that it may produce a significantly
more accurate answer.
Similar code fragments, with obvious adaptations,
may be used with all the driver routines for linear
equations listed in Table
2.2.
For example, if a symmetric system is solved using the simple driver xSYSV,
then xLANSY must be used to compute ANORM, and xSYCON must be used
to compute RCOND.
Tue Nov 29 14:03:33 EST 1994
Problems that LAPACK can Solve





Next:
Computers for which
Up:
Essentials
Previous:
LAPACK
LAPACK can solve systems of linear equations, linear least squares
problems, eigenvalue problems and singular value problems.
LAPACK can also handle many
associated computations such as matrix factorizations
or estimating condition numbers.
LAPACK contains driver routines for solving standard types of
problems,
computational routines to perform a distinct
computational task, and auxiliary routines to perform a certain
subtask or common low-level computation. Each driver routine
typically calls a sequence of
computational routines. Taken as a whole, the computational routines
can perform a wider range of tasks than are covered by the driver
routines.
Many of the auxiliary routines may be of use to numerical analysts
or software developers, so we have documented the Fortran source for
these routines with the same level of detail used for the LAPACK
routines and driver routines.
Dense and band matrices are provided for,
but not general sparse matrices. In all areas, similar functionality
is provided for real and complex matrices.
See Chapter
2 for a complete summary of the
contents.
Tue Nov 29 14:03:33 EST 1994
Further Details: Error Bounds for Linear Equation Solving





Next:
Error Bounds for
Up:
Error Bounds for
Previous:
Error Bounds for
The conventional error analysis of linear
equation
solving goes as follows.
Let Ax = b be the system to be solved. Let  be the solution
computed by LAPACK (or LINPACK) using any of their linear equation solvers.
Let r be
the residual
be the solution
computed by LAPACK (or LINPACK) using any of their linear equation solvers.
Let r be
the residual  . In the absence of rounding error r
would be zero and
. In the absence of rounding error r
would be zero and  would equal x; with rounding error one can
only say the following:
would equal x; with rounding error one can
only say the following:
The normwise backward error of the computed solution  ,
with respect to the infinity norm,
is the pair E,f which minimizes
,
with respect to the infinity norm,
is the pair E,f which minimizes
subject to the constraint  .
The minimal value of
.
The minimal value of
 is given by
is given by

One can show that the computed solution  satisfies
satisfies  ,
where p(n) is a modestly growing function of n.
The corresponding condition number is
,
where p(n) is a modestly growing function of n.
The corresponding condition number is
 .
The error
.
The error  is bounded by
is bounded by

In the first code fragment in the last section,  ,
which is
,
which is  in the numerical example,
is approximated by
in the numerical example,
is approximated by  .
Approximations
of
.
Approximations
of  - or, strictly speaking, its reciprocal RCOND -
are returned by computational routines
xyyCON (subsection
2.3.1) or driver routines
xyySVX (subsection
2.2.1). The code fragment
makes sure RCOND is at least
- or, strictly speaking, its reciprocal RCOND -
are returned by computational routines
xyyCON (subsection
2.3.1) or driver routines
xyySVX (subsection
2.2.1). The code fragment
makes sure RCOND is at least  EPSMCH to
avoid overflow in computing
ERRBD.
This limits
ERRBD to a maximum of 1, which is no loss of generality since
a relative error of 1 or more indicates the same thing:
a complete loss of accuracy.
Note that the
value of RCOND returned by xyySVX may apply to a linear
system obtained from Ax = b by equilibration, i.e.
scaling the rows and columns of A in order to make the
condition number smaller. This is the case in the second
code fragment in the last section, where the program
chose to scale the rows by the factors returned in
EPSMCH to
avoid overflow in computing
ERRBD.
This limits
ERRBD to a maximum of 1, which is no loss of generality since
a relative error of 1 or more indicates the same thing:
a complete loss of accuracy.
Note that the
value of RCOND returned by xyySVX may apply to a linear
system obtained from Ax = b by equilibration, i.e.
scaling the rows and columns of A in order to make the
condition number smaller. This is the case in the second
code fragment in the last section, where the program
chose to scale the rows by the factors returned in
 and scale the columns by the factors returned in
and scale the columns by the factors returned in
 ,
resulting in
,
resulting in  .
.
As stated in section
4.3.2,
this approach does not respect the presence
of zero or tiny entries in A. In contrast,
the LAPACK computational routines
xyyRFS (subsection
2.3.1) or driver routines xyySVX
(subsection
2.2.1) will (except in rare cases)
compute a solution  with the following properties:
with the following properties:
The componentwise backward error
of the computed solution  is the pair E,f which minimizes
is the pair E,f which minimizes

(where we interpret 0 / 0 as 0)
subject to the constraint  .
The minimal value of
.
The minimal value of  is given by
is given by

One can show that for most problems the  computed by xyySVX
satisfies
computed by xyySVX
satisfies  ,
where p(n) is a modestly growing function of n.
In other words,
,
where p(n) is a modestly growing function of n.
In other words,  is the exact solution of the
perturbed problem
is the exact solution of the
perturbed problem  where E and f are small relative perturbations in each entry of A and
b, respectively.
The corresponding condition number is
where E and f are small relative perturbations in each entry of A and
b, respectively.
The corresponding condition number is
 .
The error
.
The error  is bounded by
is bounded by

The routines xyyRFS and xyySVX return
 , which is called BERR
(for Backward ERRor),
and a bound on the the actual error
, which is called BERR
(for Backward ERRor),
and a bound on the the actual error
 , called FERR
(for Forward ERRor), as
in the second code fragment in the last section.
FERR is actually calculated by the following formula, which can
be smaller than the bound
, called FERR
(for Forward ERRor), as
in the second code fragment in the last section.
FERR is actually calculated by the following formula, which can
be smaller than the bound  given above:
given above:

Here,  is the computed value of the residual
is the computed value of the residual  , and
the norm in the numerator is estimated using the same estimation
subroutine used for RCOND.
, and
the norm in the numerator is estimated using the same estimation
subroutine used for RCOND.
The value of
BERR for the example in the last section is  .
.
Even in the rare cases where xyyRFS fails to make
BERR close to its minimum  , the error bound FERR
may remain small. See
[6]
for details.
, the error bound FERR
may remain small. See
[6]
for details.





Next:
Error Bounds for
Up:
Error Bounds for
Previous:
Error Bounds for
Tue Nov 29 14:03:33 EST 1994
Error Bounds for Linear Least Squares Problems





Next:
Further Details: Error
Up:
Accuracy and Stability
Previous:
Further Details: Error
The linear least squares problem is to find x that minimizes
 .
We discuss error bounds for the most common case where A is m-by-n
with m > n, and A has full rank
;
this is called an overdetermined least squares problem
(the following code fragments deal with m = n as well).
.
We discuss error bounds for the most common case where A is m-by-n
with m > n, and A has full rank
;
this is called an overdetermined least squares problem
(the following code fragments deal with m = n as well).
Let  be the solution computed by one of the driver routines
xGELS, xGELSX or xGELSS (see section
2.2.2).
An approximate error
bound
be the solution computed by one of the driver routines
xGELS, xGELSX or xGELSS (see section
2.2.2).
An approximate error
bound

may be computed in one of the following ways, depending on which type
of driver routine is used:
- Suppose the simple driver SGELS is used:
EPSMCH = SLAMCH( 'E' )
* Get the 2-norm of the right hand side B
BNORM = SNRM2( M, B, 1 )
* Solve the least squares problem; the solution X
* overwrites B
CALL SGELS( 'N', M, N, 1, A, LDA, B, LDB, WORK,
$ LWORK, INFO )
IF ( MIN(M,N) .GT. 0 ) THEN
* Get the 2-norm of the residual A*X-B
RNORM = SNRM2( M-N, B( N+1 ), 1 )
* Get the reciprocal condition number RCOND of A
CALL STRCON('I', 'U', 'N', N, A, LDA, RCOND,
$ WORK, IWORK, INFO)
RCOND = MAX( RCOND, EPSMCH )
IF ( BNORM .GT. 0.0 ) THEN
SINT = RNORM / BNORM
ELSE
SINT = 0.0
ENDIF
COST = MAX( SQRT( (1.0E0 - SINT)*(1.0E0 + SINT) ),
$ EPSMCH )
TANT = SINT / COST
ERRBD = EPSMCH*( 2.0E0/(RCOND*COST) +
$ TANT / RCOND**2 )
ENDIF
For example,
if  ,
,

then, to 4 decimal places,

 ,
,
 ,
,
 ,
,
 , and the true error
is
, and the true error
is  .
.
- Suppose the expert driver SGELSX is used.
This routine has an input argument RCND,
which is used to determine the rank of the input matrix (briefly,
the matrix is considered not to have full rank if its condition
number exceeds 1/RCND).
The code fragment below only computes error bounds
if the matrix has been determined to have full rank.
When the matrix does not have full rank,
computing and interpreting error bounds is more complicated, and
the reader is referred to the next section.
EPSMCH = SLAMCH( 'E' )
* Get the 2-norm of the right hand side B
BNORM = SNRM2( M, B, 1 )
* Solve the least squares problem; the solution X
* overwrites B
RCND = 0
CALL SGELSX( M, N, 1, A, LDA, B, LDB, JPVT, RCND,
$ RANK, WORK, INFO )
IF ( RANK.LT.N ) THEN
PRINT *,'Matrix less than full rank'
ELSE IF ( MIN( M,N ) .GT. 0 ) THEN
* Get the 2-norm of the residual A*X-B
RNORM = SNRM2( M-N, B( N+1 ), 1 )
* Get the reciprocal condition number RCOND of A
CALL STRCON('I', 'U', 'N', N, A, LDA, RCOND,
$ WORK, IWORK, INFO)
RCOND = MAX( RCOND, EPSMCH )
IF ( BNORM .GT. 0.0 ) THEN
SINT = RNORM / BNORM
ELSE
SINT = 0.0
ENDIF
COST = MAX( SQRT( (1.0E0 - SINT)*(1.0E0 + SINT) ),
$ EPSMCH )
TANT = SINT / COST
ERRBD = EPSMCH*( 2.0E0/(RCOND*COST) +
$ TANT / RCOND**2 )
END IF
The numerical results of this code fragment on the above A and b are
the same as for the first code fragment.
- Suppose the other type of expert driver SGELSS is used
.
This routine also has an input argument RCND, which is used to
determine the rank of the matrix A. The same code fragment can be used
to compute error bounds as for SGELSX, except that the call to SGELSX must
be replaced by:
CALL SGELSS( M, N, 1, A, LDA, B, LDB, S, RCND, RANK,
$ WORK, LWORK, INFO )
and the call to STRCON must be replaced by:
RCOND = S( N ) / S( 1 )
Applied to the same A and b as above, the computed  is
nearly the same,
is
nearly the same,
 ,
,
 , and the true error is
, and the true error is
 .
.





Next:
Further Details: Error
Up:
Accuracy and Stability
Previous:
Further Details: Error
Tue Nov 29 14:03:33 EST 1994
Further Details: Error Bounds for Linear Least Squares
Problems





Next:
Error Bounds for
Up:
Error Bounds for
Previous:
Error Bounds for
The conventional error analysis of linear least squares problems goes
as follows
.
As above, let  be the solution to minimizing
be the solution to minimizing
 computed by
LAPACK using one of the least squares drivers xGELS, xGELSS or xGELSX
(see subsection
2.2.2).
We discuss the most common case, where A is
overdetermined
(i.e., has more rows than columns) and has full rank
[45]:
computed by
LAPACK using one of the least squares drivers xGELS, xGELSS or xGELSX
(see subsection
2.2.2).
We discuss the most common case, where A is
overdetermined
(i.e., has more rows than columns) and has full rank
[45]:
The computed solution  has a small normwise backward error.
In other words
has a small normwise backward error.
In other words  minimizes
minimizes  , where
E and f satisfy
, where
E and f satisfy

and p(n) is a modestly growing function of n. We take p(n) = 1 in
the code fragments above.
Let  (approximated by
1/RCOND in the above code fragments),
(approximated by
1/RCOND in the above code fragments),
 (= RNORM above), and
(= RNORM above), and  (SINT = RNORM / BNORM above). Here,
(SINT = RNORM / BNORM above). Here,  is the acute angle between
the vectors
is the acute angle between
the vectors  and
and  .
Then when
.
Then when  is small, the error
is small, the error  is bounded by
is bounded by

where  = COST and
= COST and  = TANT in the code fragments
above.
= TANT in the code fragments
above.
We avoid overflow by making sure RCOND and COST are both at least
 EPSMCH, and by handling the case of a zero B matrix
separately (BNORM = 0).
EPSMCH, and by handling the case of a zero B matrix
separately (BNORM = 0).
 may be computed directly
from the singular values of A returned by xGELSS (as in the code fragment) or
by xGESVD. It may also be approximated by using xTRCON following calls to
xGELS or xGELSX. xTRCON estimates
may be computed directly
from the singular values of A returned by xGELSS (as in the code fragment) or
by xGESVD. It may also be approximated by using xTRCON following calls to
xGELS or xGELSX. xTRCON estimates  or
or  instead
of
instead
of  , but these can differ from
, but these can differ from  by at most a factor of n.
by at most a factor of n.
If A is rank-deficient, xGELSS and xGELSX can be used to regularize the
problem
by treating all singular values
less than a user-specified threshold
( ) as
exactly zero. The number of singular values treated as nonzero is returned
in RANK. See
[45] for error bounds in this case, as well as
[45]
[19] for the
underdetermined
case.
) as
exactly zero. The number of singular values treated as nonzero is returned
in RANK. See
[45] for error bounds in this case, as well as
[45]
[19] for the
underdetermined
case.
The solution of the overdetermined,
full-rank problem may also be
characterized as the solution of the linear system of equations

By solving this linear system using xyyRFS or xyySVX (see section
4.4) componentwise error bounds can also be obtained
[7].





Next:
Error Bounds for
Up:
Error Bounds for
Previous:
Error Bounds for
Tue Nov 29 14:03:33 EST 1994
Error Bounds for Generalized Least Squares Problems





Next:
Error Bounds for
Up:
Accuracy and Stability
Previous:
Further Details: Error
There are two kinds of generalized least squares problems that are discussed in
section
2.2.3: the linear equality-constrained least squares
problem, and the general linear model problem. Error bounds for
these problems will be included in a future version of this manual.
Tue Nov 29 14:03:33 EST 1994
Error Bounds for the Symmetric Eigenproblem





Next:
Further Details: Error
Up:
Accuracy and Stability
Previous:
Error Bounds for
The eigendecomposition
of
an n-by-n real symmetric matrix is the
factorization  (
( in the complex Hermitian
case), where Z is orthogonal (unitary) and
in the complex Hermitian
case), where Z is orthogonal (unitary) and
 is real and diagonal,
with
is real and diagonal,
with  .
The
.
The  are the eigenvalues
of Aand the columns
are the eigenvalues
of Aand the columns  of
Z are the eigenvectors
. This is also often written
of
Z are the eigenvectors
. This is also often written
 . The eigendecomposition of a symmetric matrix is
computed
by the driver routines xSYEV, xSYEVX, xSYEVD, xSBEV, xSBEVX, xSBEVD,
xSPEV, xSPEVX, xSPEVD, xSTEV, xSTEVX and xSTEVD.
The complex counterparts of these routines, which compute the
eigendecomposition of complex Hermitian matrices, are
the driver routines xHEEV, xHEEVX, xHEEVD, xHBEV, xHBEVX, xHBEVD,
xHPEV, xHPEVX, and xHPEVD (see subsection
2.2.4).
. The eigendecomposition of a symmetric matrix is
computed
by the driver routines xSYEV, xSYEVX, xSYEVD, xSBEV, xSBEVX, xSBEVD,
xSPEV, xSPEVX, xSPEVD, xSTEV, xSTEVX and xSTEVD.
The complex counterparts of these routines, which compute the
eigendecomposition of complex Hermitian matrices, are
the driver routines xHEEV, xHEEVX, xHEEVD, xHBEV, xHBEVX, xHBEVD,
xHPEV, xHPEVX, and xHPEVD (see subsection
2.2.4).
The approximate error
bounds
for the computed eigenvalues
 are
are

The approximate error bounds for the computed eigenvectors
 , which bound the acute angles
between the computed eigenvectors and true
eigenvectors
, which bound the acute angles
between the computed eigenvectors and true
eigenvectors  , are:
, are:

These bounds can be computed by the following code fragment:
EPSMCH = SLAMCH( 'E' )
* Compute eigenvalues and eigenvectors of A
* The eigenvalues are returned in W
* The eigenvector matrix Z overwrites A
CALL SSYEV( 'V', UPLO, N, A, LDA, W, WORK, LWORK, INFO )
IF( INFO.GT.0 ) THEN
PRINT *,'SSYEV did not converge'
ELSE IF ( N.GT.0 ) THEN
* Compute the norm of A
ANORM = MAX( ABS( W(1) ), ABS( W(N) ) )
EERRBD = EPSMCH * ANORM
* Compute reciprocal condition numbers for eigenvectors
CALL SDISNA( 'Eigenvectors', N, N, W, RCONDZ, INFO )
DO 10 I = 1, N
ZERRBD( I ) = EPSMCH * ( ANORM / RCONDZ( I ) )
10 CONTINUE
ENDIF
For example,
if  and
and

then the eigenvalues, approximate error bounds, and true errors are

Tue Nov 29 14:03:33 EST 1994
Further Details: Error Bounds for the Symmetric Eigenproblem





Next:
Error Bounds for
Up:
Error Bounds for
Previous:
Error Bounds for
The usual error analysis of the
symmetric
eigenproblem (using any LAPACK
routine in subsection
2.2.4
or any EISPACK routine) is as follows
[64]:
The computed eigendecomposition  is nearly
the exact
eigendecomposition of A + E, i.e.,
is nearly
the exact
eigendecomposition of A + E, i.e.,
 is a true eigendecomposition so that
is a true eigendecomposition so that  is
orthogonal,
where
is
orthogonal,
where  and
and
 . Here p(n) is a modestly growing
function of n. We take p(n) = 1 in the above code fragment.
Each computed eigenvalue
. Here p(n) is a modestly growing
function of n. We take p(n) = 1 in the above code fragment.
Each computed eigenvalue  differs from a
true
differs from a
true  by at most
by at most
Thus large eigenvalues (those near  )
are computed to high relative accuracy
and small ones may not be.
)
are computed to high relative accuracy
and small ones may not be.
The angular difference between the computed unit eigenvector
 and a true unit eigenvector
and a true unit eigenvector  satisfies the approximate bound
satisfies the approximate bound

if  is small enough.
Here
is small enough.
Here  is the
absolute gap
between
is the
absolute gap
between  and the nearest other eigenvalue. Thus, if
and the nearest other eigenvalue. Thus, if  is close to other eigenvalues, its corresponding eigenvector
is close to other eigenvalues, its corresponding eigenvector  may be inaccurate.
The gaps may be easily computed from the array of computed eigenvalues
using subroutine SDISNA
.
The gaps computed by SDISNA are ensured not to be so small as
to cause overflow when used as divisors.
may be inaccurate.
The gaps may be easily computed from the array of computed eigenvalues
using subroutine SDISNA
.
The gaps computed by SDISNA are ensured not to be so small as
to cause overflow when used as divisors.
Let  be the invariant subspace spanned by a collection of eigenvectors
be the invariant subspace spanned by a collection of eigenvectors
 , where
, where  is a subset of the
integers from 1 to n. Let S be the corresponding true subspace. Then
is a subset of the
integers from 1 to n. Let S be the corresponding true subspace. Then

where

is the absolute gap between the eigenvalues in  and the nearest
other eigenvalue. Thus, a cluster
of
close eigenvalues which is
far away from any other eigenvalue may have a well determined
invariant subspace
and the nearest
other eigenvalue. Thus, a cluster
of
close eigenvalues which is
far away from any other eigenvalue may have a well determined
invariant subspace  even if its individual eigenvectors are
ill-conditioned
even if its individual eigenvectors are
ill-conditioned
 .
.
In the special case of a real symmetric tridiagonal matrix T, the eigenvalues
and eigenvectors can be computed much more accurately. xSYEV (and the other
symmetric eigenproblem drivers) computes the eigenvalues and eigenvectors of
a dense symmetric matrix by first reducing it to tridiagonal form
T, and then
finding the eigenvalues and eigenvectors of T.
Reduction of a dense matrix to tridiagonal form
T can introduce
additional errors, so the following bounds for the tridiagonal case do not
apply to the dense case.
The eigenvalues of T may be computed with small componentwise relative
backward error
( ) by using subroutine xSTEBZ (subsection
2.3.4)
or driver xSTEVX (subsection
2.2.4). If T is also positive definite,
they may also be computed at least as accurately by xPTEQR
(subsection
2.3.4).
To compute error bounds
for the computed eigenvalues
) by using subroutine xSTEBZ (subsection
2.3.4)
or driver xSTEVX (subsection
2.2.4). If T is also positive definite,
they may also be computed at least as accurately by xPTEQR
(subsection
2.3.4).
To compute error bounds
for the computed eigenvalues  we must make some assumptions
about T. The bounds discussed here are from
[13].
Suppose T is positive definite, and
write T = DHD where
we must make some assumptions
about T. The bounds discussed here are from
[13].
Suppose T is positive definite, and
write T = DHD where  and
and  .
Then the computed eigenvalues
.
Then the computed eigenvalues
 can differ from true eigenvalues
can differ from true eigenvalues  by
by
where p(n) is a modestly growing function of n.
Thus if  is moderate, each eigenvalue will be computed
to high relative accuracy,
no matter how tiny it is.
The eigenvectors
is moderate, each eigenvalue will be computed
to high relative accuracy,
no matter how tiny it is.
The eigenvectors  computed by xPTEQR
can differ from true eigenvectors
computed by xPTEQR
can differ from true eigenvectors  by
at most about
by
at most about

if  is small enough, where
is small enough, where
 is the relative gap between
is the relative gap between  and the nearest other eigenvalue.
Since the relative gap may be much larger than the absolute gap, this
error bound may be much smaller than the previous one.
and the nearest other eigenvalue.
Since the relative gap may be much larger than the absolute gap, this
error bound may be much smaller than the previous one.
 could be computed by applying
xPTCON (subsection
2.3.1) to H.
The relative gaps are easily computed from the
array of computed eigenvalues.
could be computed by applying
xPTCON (subsection
2.3.1) to H.
The relative gaps are easily computed from the
array of computed eigenvalues.
Jacobi's method
[69]
[76]
[24] is another
algorithm for finding eigenvalues and eigenvectors of symmetric matrices. It is
slower than the algorithms based on first tridiagonalizing the matrix, but is
capable of computing more accurate answers in several important cases. Routines
implementing Jacobi's method and corresponding error bounds will be available
in a future LAPACK release.





Next:
Error Bounds for
Up:
Error Bounds for
Previous:
Error Bounds for
Tue Nov 29 14:03:33 EST 1994
Error Bounds for the Nonsymmetric Eigenproblem





Next:
Further Details: Error
Up:
Accuracy and Stability
Previous:
Further Details: Error
The nonsymmetric eigenvalue
problem
is more
complicated than the
symmetric eigenvalue problem. In this subsection,
we state the simplest bounds and leave the more complicated ones to
subsequent subsections.
Let A be an n-by-n nonsymmetric matrix, with eigenvalues
 . Let
. Let  be a right eigenvector
corresponding to
be a right eigenvector
corresponding to  :
:  .
Let
.
Let  and
and  be the corresponding
computed eigenvalues and eigenvectors, computed by expert driver routine
xGEEVX (see subsection
2.2.4).
be the corresponding
computed eigenvalues and eigenvectors, computed by expert driver routine
xGEEVX (see subsection
2.2.4).
The approximate error bounds
for the computed eigenvalues are

The approximate error
bounds
for the computed eigenvectors  ,
which bound the acute angles between the computed eigenvectors and true
eigenvectors
,
which bound the acute angles between the computed eigenvectors and true
eigenvectors  , are
, are

These bounds can be computed by the following code fragment:
EPSMCH = SLAMCH( 'E' )
* Compute the eigenvalues and eigenvectors of A
* WR contains the real parts of the eigenvalues
* WI contains the real parts of the eigenvalues
* VL contains the left eigenvectors
* VR contains the right eigenvectors
CALL SGEEVX( 'P', 'V', 'V', 'B', N, A, LDA, WR, WI,
$ VL, LDVL, VR, LDVR, ILO, IHI, SCALE, ABNRM,
$ RCONDE, RCONDV, WORK, LWORK, IWORK, INFO )
IF( INFO.GT.0 ) THEN
PRINT *,'SGEEVX did not converge'
ELSE IF ( N.GT.0 ) THEN
DO 10 I = 1, N
EERRBD(I) = EPSMCH*ABNRM/RCONDE(I)
VERRBD(I) = EPSMCH*ABNRM/RCONDV(I)
10 CONTINUE
ENDIF
For example, if
 and
and

then true eigenvalues, approximate eigenvalues, approximate error bounds,
and true errors are

Tue Nov 29 14:03:33 EST 1994
Further Details: Error Bounds for the Nonsymmetric Eigenproblem





Next:
Overview
Up:
Error Bounds for
Previous:
Error Bounds for
Tue Nov 29 14:03:33 EST 1994
Overview





Next:
Balancing and Conditioning
Up:
Further Details: Error
Previous:
Further Details: Error
In this subsection, we will summarize all the available error bounds.
Later subsections will provide further details. The reader may also
refer to
[11].
Bounds for individual eigenvalues and eigenvectors are provided by
driver xGEEVX (subsection
2.2.4) or computational
routine xTRSNA (subsection
2.3.5).
Bounds for
clusters
of eigenvalues
and their associated invariant subspace are
provided by driver xGEESX (subsection
2.2.4) or
computational routine xTRSEN (subsection
2.3.5).
We let  be the i-th computed eigenvalue and
be the i-th computed eigenvalue and
 an i-th true eigenvalue.
an i-th true eigenvalue.
 Let
Let  be the
corresponding computed right eigenvector, and
be the
corresponding computed right eigenvector, and  a true right
eigenvector (so
a true right
eigenvector (so  ).
If
).
If  is a subset of the
integers from 1 to n, we let
is a subset of the
integers from 1 to n, we let  denote the average of
the selected eigenvalues:
denote the average of
the selected eigenvalues:
 ,
and similarly for
,
and similarly for  . We also let
. We also let  denote the subspace spanned by
denote the subspace spanned by  ; it is
called a right invariant subspace because if v is any vector in
; it is
called a right invariant subspace because if v is any vector in  then
Av is also in
then
Av is also in  .
.  is the corresponding computed subspace.
is the corresponding computed subspace.
The algorithms for the nonsymmetric eigenproblem are normwise backward stable:
they compute the exact eigenvalues, eigenvectors and invariant subspaces
of slightly perturbed matrices A + E, where  .
Some of the bounds are stated in terms of
.
Some of the bounds are stated in terms of  and others in
terms of
and others in
terms of  ; one may use
; one may use  to approximate
either quantity.
The code fragment in the previous subsection approximates
to approximate
either quantity.
The code fragment in the previous subsection approximates
 by
by  , where
, where  is returned by xGEEVX.
is returned by xGEEVX.
xGEEVX (or xTRSNA) returns two quantities for each
 ,
,  pair:
pair:  and
and  .
xGEESX (or xTRSEN) returns two quantities for a selected subset
.
xGEESX (or xTRSEN) returns two quantities for a selected subset
 of eigenvalues:
of eigenvalues:  and
and  .
.
 (or
(or  ) is a reciprocal condition number for the
computed eigenvalue
) is a reciprocal condition number for the
computed eigenvalue  (or
(or  ),
and is referred to as RCONDE by xGEEVX (or xGEESX).
),
and is referred to as RCONDE by xGEEVX (or xGEESX).
 (or
(or  ) is a reciprocal condition number for
the right eigenvector
) is a reciprocal condition number for
the right eigenvector  (or
(or  ), and
is referred to as RCONDV by xGEEVX (or xGEESX).
The approximate error bounds for eigenvalues, averages of eigenvalues,
eigenvectors, and invariant subspaces
provided in Table
4.5 are
true for sufficiently small ||E||, which is why they are called asymptotic.
), and
is referred to as RCONDV by xGEEVX (or xGEESX).
The approximate error bounds for eigenvalues, averages of eigenvalues,
eigenvectors, and invariant subspaces
provided in Table
4.5 are
true for sufficiently small ||E||, which is why they are called asymptotic.

Table 4.5: Asymptotic error bounds for the nonsymmetric eigenproblem
If the problem is ill-conditioned, the asymptotic bounds may only hold
for extremely small ||E||. Therefore, in Table
4.6
we also provide global bounds
which are guaranteed to hold for all  .
.

Table 4.6: Global error bounds for the nonsymmetric eigenproblem
assuming 
We also have the following bound, which is true for all E:
all the  lie in the union of n disks,
where the i-th disk is centered at
lie in the union of n disks,
where the i-th disk is centered at  and has
radius
and has
radius  . If k of these disks overlap,
so that any two points inside the k disks can be connected
by a continuous curve lying entirely inside the k disks,
and if no larger set of k + 1 disks has this property,
then exactly k of the
. If k of these disks overlap,
so that any two points inside the k disks can be connected
by a continuous curve lying entirely inside the k disks,
and if no larger set of k + 1 disks has this property,
then exactly k of the  lie inside the
union of these k disks. Figure
4.1 illustrates
this for a 10-by-10 matrix, with 4 such overlapping unions
of disks, two containing 1 eigenvalue each, one containing 2
eigenvalues, and one containing 6 eigenvalues.
lie inside the
union of these k disks. Figure
4.1 illustrates
this for a 10-by-10 matrix, with 4 such overlapping unions
of disks, two containing 1 eigenvalue each, one containing 2
eigenvalues, and one containing 6 eigenvalues.

Figure 4.1: Bounding eigenvalues inside overlapping disks
Finally, the quantities s and sep tell use how we can best
(block) diagonalize a matrix A by a similarity,
 , where each diagonal block
, where each diagonal block
 has a selected subset of the eigenvalues of A. Such a decomposition
may be useful in computing functions of matrices, for example.
The goal is to choose a V with a nearly minimum condition number
has a selected subset of the eigenvalues of A. Such a decomposition
may be useful in computing functions of matrices, for example.
The goal is to choose a V with a nearly minimum condition number
 which performs this decomposition, since this generally minimizes the error
in the decomposition.
This may be done as follows. Let
which performs this decomposition, since this generally minimizes the error
in the decomposition.
This may be done as follows. Let  be
be
 -by-
-by- . Then columns
. Then columns  through
through
 of V span the invariant
subspace
of A corresponding
to the eigenvalues of
of V span the invariant
subspace
of A corresponding
to the eigenvalues of  ; these columns should be chosen to be any
orthonormal basis of this space (as computed by xGEESX, for example).
Let
; these columns should be chosen to be any
orthonormal basis of this space (as computed by xGEESX, for example).
Let  be the value corresponding to the
cluster of
eigenvalues of
be the value corresponding to the
cluster of
eigenvalues of  , as computed by xGEESX or xTRSEN. Then
, as computed by xGEESX or xTRSEN. Then
 , and no other choice of V can make
its condition number smaller than
, and no other choice of V can make
its condition number smaller than  [17].
Thus choosing orthonormal
subblocks of V gets
[17].
Thus choosing orthonormal
subblocks of V gets  to within a factor b of its minimum
value.
to within a factor b of its minimum
value.
In the case of a real symmetric (or complex Hermitian) matrix,
s = 1 and sep is the absolute gap, as defined in subsection
4.7.
The bounds in Table
4.5 then reduce to the
bounds in subsection
4.7.





Next:
Balancing and Conditioning
Up:
Further Details: Error
Previous:
Further Details: Error
Tue Nov 29 14:03:33 EST 1994
Balancing and Conditioning





Next:
Computing and
Up:
Further Details: Error
Previous:
Overview
There are two preprocessing
steps
one may perform
on a matrix A in order
to make its eigenproblem easier. The first is permutation, or
reordering the rows and columns to make A more nearly upper triangular
(closer to Schur form):  , where P is a permutation matrix.
If
, where P is a permutation matrix.
If  is permutable to upper triangular form (or close to it), then
no floating-point operations (or very few) are needed to reduce it to
Schur form.
The second is scaling
by a diagonal matrix D to make the rows and
columns of
is permutable to upper triangular form (or close to it), then
no floating-point operations (or very few) are needed to reduce it to
Schur form.
The second is scaling
by a diagonal matrix D to make the rows and
columns of  more nearly equal in norm:
more nearly equal in norm:  . Scaling
can make the matrix norm smaller with respect to the eigenvalues, and so
possibly reduce the inaccuracy contributed by roundoff
[][Chap. II/11]wilkinson3. We refer to these two operations as
.
. Scaling
can make the matrix norm smaller with respect to the eigenvalues, and so
possibly reduce the inaccuracy contributed by roundoff
[][Chap. II/11]wilkinson3. We refer to these two operations as
.
Balancing is performed by driver xGEEVX, which calls
computational routine xGEBAL. The user may tell xGEEVX to optionally
permute, scale, do both, or do neither; this is specified by input
parameter BALANC. Permuting has no effect on
the condition numbers
or their interpretation as described in previous
subsections. Scaling, however, does change their interpretation,
as we now describe.
The output parameters of xGEEVX - SCALE (real array of length N),
ILO (integer), IHI (integer) and ABNRM (real) - describe
the result of
balancing a matrix A into  , where N is the dimension of A.
The matrix
, where N is the dimension of A.
The matrix  is block upper triangular, with at most three blocks:
from 1 to ILO - 1, from ILO to IHI, and from IHI + 1 to N.
The first and last blocks are upper triangular, and so already in Schur
form. These are not scaled; only the block from ILO to IHI is scaled.
Details of the scaling and permutation are described in SCALE (see the
specification of xGEEVX or xGEBAL for details)
. The one-norm of
is block upper triangular, with at most three blocks:
from 1 to ILO - 1, from ILO to IHI, and from IHI + 1 to N.
The first and last blocks are upper triangular, and so already in Schur
form. These are not scaled; only the block from ILO to IHI is scaled.
Details of the scaling and permutation are described in SCALE (see the
specification of xGEEVX or xGEBAL for details)
. The one-norm of
 is returned in ABNRM.
is returned in ABNRM.
The condition numbers
described in earlier subsections are computed for
the balanced matrix  , and so some interpretation is needed to
apply them to the eigenvalues and eigenvectors of the original matrix A.
To use the bounds for eigenvalues in Tables
4.5 and
4.6,
we must replace
, and so some interpretation is needed to
apply them to the eigenvalues and eigenvectors of the original matrix A.
To use the bounds for eigenvalues in Tables
4.5 and
4.6,
we must replace  and
and  by
by  . To use the
bounds for eigenvectors, we also need to take into account that bounds
on rotations of eigenvectors are for the eigenvectors
. To use the
bounds for eigenvectors, we also need to take into account that bounds
on rotations of eigenvectors are for the eigenvectors  of
of
 , which are related to the eigenvectors x of A by
, which are related to the eigenvectors x of A by
 , or
, or  . One coarse but simple way to do this is
as follows: let
. One coarse but simple way to do this is
as follows: let  be the bound on rotations of
be the bound on rotations of  from
Table
4.5 or Table
4.6
and let
from
Table
4.5 or Table
4.6
and let  be the desired bound on rotation of x. Let
be the desired bound on rotation of x. Let

be the condition number of D.
Then

The numerical example in subsection
4.8 does no scaling,
just permutation.





Next:
Computing and
Up:
Further Details: Error
Previous:
Overview
Tue Nov 29 14:03:33 EST 1994
Computers for which LAPACK is Suitable





Next:
LAPACK Compared with
Up:
Essentials
Previous:
Problems that LAPACK
LAPACK is designed to give high efficiency
on vector processors,
high-performance ``super-scalar'' workstations, and
shared memory multiprocessors.
LAPACK in its present form
is less likely to give good performance on other types of
parallel architectures (for example,
massively parallel SIMD machines, or distributed memory machines),
but work has begun to try to adapt LAPACK to these new
architectures.
LAPACK can also be used satisfactorily on all types of scalar machines
(PC's, workstations, mainframes).
See Chapter
3 for some examples of the
performance achieved by LAPACK routines.
Tue Nov 29 14:03:33 EST 1994
Computing <var>s</var> and <var>sep</var>





Next:
Error Bounds for
Up:
Further Details: Error
Previous:
Balancing and Conditioning
To explain s and sep
, we need to
introduce
the spectral projector P
[56]
[72], and the
separation of two matrices
A and B, sep(A , B)
[75]
[72].
We may assume the matrix A is in Schur form, because reducing it
to this form does not change the values of s and sep.
Consider a cluster of m > = 1 eigenvalues, counting multiplicities.
Further assume the n-by-n matrix A is

where the eigenvalues of the m-by-n matrix
 are exactly those in which we are
interested. In practice, if the eigenvalues on the diagonal of A
are in the wrong order, routine xTREXC
can be used to put the desired ones in the upper left corner
as shown.
are exactly those in which we are
interested. In practice, if the eigenvalues on the diagonal of A
are in the wrong order, routine xTREXC
can be used to put the desired ones in the upper left corner
as shown.
We define the spectral projector, or simply projector P belonging
to the eigenvalues of  as
as

where R satisfies the system of linear equations

Equation (
4.3) is called a Sylvester equation
.
Given the Schur form (
4.1), we solve equation
(
4.3) for R using the subroutine xTRSYL.
We can now define s for the eigenvalues of  :
:

In practice we do not use this expression since  is hard to
compute. Instead we use the more easily computed underestimate
is hard to
compute. Instead we use the more easily computed underestimate

which can underestimate the true value of s by no more than a factor
 .
This underestimation makes our error bounds more conservative.
This approximation of s is called RCONDE in xGEEVX and xGEESX.
.
This underestimation makes our error bounds more conservative.
This approximation of s is called RCONDE in xGEEVX and xGEESX.
The separation  of the matrices
of the matrices  and
and
 is defined as the smallest singular value of the linear
map in (
4.3) which takes X to
is defined as the smallest singular value of the linear
map in (
4.3) which takes X to  , i.e.,
, i.e.,

This formulation lets us estimate  using the condition estimator
xLACON
[52]
[51]
[48], which estimates the norm of
a linear operator
using the condition estimator
xLACON
[52]
[51]
[48], which estimates the norm of
a linear operator  given the ability to compute T and
given the ability to compute T and
 quickly for arbitrary x.
In our case, multiplying an
arbitrary vector by T
means solving the Sylvester equation (
4.3)
with an arbitrary right hand side using xTRSYL, and multiplying by
quickly for arbitrary x.
In our case, multiplying an
arbitrary vector by T
means solving the Sylvester equation (
4.3)
with an arbitrary right hand side using xTRSYL, and multiplying by
 means solving the same equation with
means solving the same equation with  replaced by
replaced by
 and
and  replaced by
replaced by  . Solving either equation
costs at most
. Solving either equation
costs at most  operations, or as few as
operations, or as few as  if m << n.
Since the true value of sep is
if m << n.
Since the true value of sep is  but we use
but we use  ,
our estimate of sep may differ from the true value by as much as
,
our estimate of sep may differ from the true value by as much as
 . This approximation to sep is called
RCONDV by xGEEVX and xGEESX.
. This approximation to sep is called
RCONDV by xGEEVX and xGEESX.
Another formulation which in principle permits an exact evaluation of
 is
is

where  is the Kronecker product of X and Y.
This method is
generally impractical, however, because the matrix whose smallest singular
value we need is m(n - m) dimensional, which can be as large as
is the Kronecker product of X and Y.
This method is
generally impractical, however, because the matrix whose smallest singular
value we need is m(n - m) dimensional, which can be as large as
 . Thus we would require as much as
. Thus we would require as much as  extra workspace and
extra workspace and
 operations, much more than the estimation method of the last
paragraph.
operations, much more than the estimation method of the last
paragraph.
The expression  measures the ``separation'' of
the spectra
of
measures the ``separation'' of
the spectra
of  and
and  in the following sense. It is zero if and only if
in the following sense. It is zero if and only if
 and
and  have a common eigenvalue, and small if there is a small
perturbation of either one that makes them have a common eigenvalue. If
have a common eigenvalue, and small if there is a small
perturbation of either one that makes them have a common eigenvalue. If
 and
and  are both Hermitian matrices, then
are both Hermitian matrices, then  is just the gap, or minimum distance between an eigenvalue of
is just the gap, or minimum distance between an eigenvalue of  and an
eigenvalue of
and an
eigenvalue of  . On the other hand, if
. On the other hand, if  and
and  are
non-Hermitian,
are
non-Hermitian,  may be much smaller than
this gap.
may be much smaller than
this gap.





Next:
Error Bounds for
Up:
Further Details: Error
Previous:
Balancing and Conditioning
Tue Nov 29 14:03:33 EST 1994
Error Bounds for the Singular Value Decomposition





Next:
Further Details: Error
Up:
Accuracy and Stability
Previous:
Computing and
The singular
value decomposition (SVD) of a
real m-by-n matrix A is defined as follows. Let r = min(m , n).
The the SVD of A is  (
( in the complex case),
where
U and V are orthogonal (unitary) matrices and
in the complex case),
where
U and V are orthogonal (unitary) matrices and
 is diagonal,
with
is diagonal,
with  .
The
.
The  are the singular values of A and the leading
r columns
are the singular values of A and the leading
r columns  of U and
of U and  of V the
left and right singular vectors, respectively.
The SVD of a general matrix is computed by xGESVD
(see subsection
2.2.4).
of V the
left and right singular vectors, respectively.
The SVD of a general matrix is computed by xGESVD
(see subsection
2.2.4).
The approximate error
bounds
for the computed singular values
 are
are

The approximate error bounds for the computed singular vectors
 and
and  ,
which bound the acute angles between the computed singular vectors and true
singular vectors
,
which bound the acute angles between the computed singular vectors and true
singular vectors  and
and  , are
, are

These bounds can be computing by the following code fragment.
EPSMCH = SLAMCH( 'E' )
* Compute singular value decomposition of A
* The singular values are returned in S
* The left singular vectors are returned in U
* The transposed right singular vectors are returned in VT
CALL SGESVD( 'S', 'S', M, N, A, LDA, S, U, LDU, VT, LDVT,
$ WORK, LWORK, INFO )
IF( INFO.GT.0 ) THEN
PRINT *,'SGESVD did not converge'
ELSE IF ( MIN(M,N) .GT. 0 ) THEN
SERRBD = EPSMCH * S(1)
* Compute reciprocal condition numbers for singular
* vectors
CALL SDISNA( 'Left', M, N, S, RCONDU, INFO )
CALL SDISNA( 'Right', M, N, S, RCONDV, INFO )
DO 10 I = 1, MIN(M,N)
VERRBD( I ) = EPSMCH*( S(1)/RCONDV( I ) )
UERRBD( I ) = EPSMCH*( S(1)/RCONDU( I ) )
10 CONTINUE
END IF
For example,
if
 and
and

then the singular values, approximate error bounds, and true errors are given below.

Tue Nov 29 14:03:33 EST 1994
Further Details: Error Bounds for the Singular Value Decomposition





Next:
Error Bounds for
Up:
Error Bounds for
Previous:
Error Bounds for
The usual error analysis of the SVD algorithm
xGESVD in LAPACK (see
subsection
2.2.4) or the
routines in LINPACK and EISPACK is as follows
[45]:
The SVD algorithm is backward stable.
This means that the computed SVD,  ,
is nearly the exact SVD of A + E where
,
is nearly the exact SVD of A + E where  ,
and p(m , n) is a modestly growing function of m and n. This means
,
and p(m , n) is a modestly growing function of m and n. This means
 is the true SVD, so that
is the true SVD, so that  and
and  are both orthogonal, where
are both orthogonal, where
 , and
, and
 .
Each computed singular value
.
Each computed singular value  differs from true
differs from true  by at most
by at most
(we take p(m , n) = 1 in the code fragment).
Thus large singular values (those near  ) are computed to
high relative accuracy
and small ones may not be.
) are computed to
high relative accuracy
and small ones may not be.
The angular difference between the computed left singular vector  and a true
and a true  satisfies the approximate bound
satisfies the approximate bound

where  is the
absolute gap
between
is the
absolute gap
between  and the nearest other singular value.
We take p(m , n) = 1 in the code fragment.
Thus, if
and the nearest other singular value.
We take p(m , n) = 1 in the code fragment.
Thus, if  is close to other singular values, its corresponding singular vector
is close to other singular values, its corresponding singular vector  may be inaccurate. When n > m, then
may be inaccurate. When n > m, then  must be redefined
as
must be redefined
as  .
The gaps may be easily computed from the array of computed singular values
using function
SDISNA.
The gaps computed by SDISNA are ensured not to be so small as
to cause overflow when used as divisors.
The same bound applies to the computed right singular
vector
.
The gaps may be easily computed from the array of computed singular values
using function
SDISNA.
The gaps computed by SDISNA are ensured not to be so small as
to cause overflow when used as divisors.
The same bound applies to the computed right singular
vector  and a true vector
and a true vector  .
.
Let  be the space spanned by a collection of computed left singular
vectors
be the space spanned by a collection of computed left singular
vectors  , where
, where  is a subset
of the integers from 1 to n. Let S be the corresponding true space.
Then
is a subset
of the integers from 1 to n. Let S be the corresponding true space.
Then

where

is the absolute gap between the singular values in  and the nearest
other singular value. Thus, a cluster
of close singular values which is
far away from any other singular value may have a well determined
space
and the nearest
other singular value. Thus, a cluster
of close singular values which is
far away from any other singular value may have a well determined
space  even if its individual singular vectors are ill-conditioned.
The same bound applies to a set of right singular vectors
even if its individual singular vectors are ill-conditioned.
The same bound applies to a set of right singular vectors

 .
.
In the special case of bidiagonal matrices, the singular values and
singular vectors may be computed much more accurately. A bidiagonal
matrix B has nonzero entries only on the main diagonal and the diagonal
immediately
above it (or immediately below it). xGESVD computes the SVD of a general
matrix by first reducing it to bidiagonal form B, and then calling xBDSQR
(subsection
2.3.6)
to compute the SVD of B.
Reduction of a dense matrix to bidiagonal form B can introduce
additional errors, so the following bounds for the bidiagonal case
do not apply to the dense case.
Each computed singular value of a bidiagonal matrix
is accurate to nearly full relative accuracy
,
no matter how tiny it is:
The computed left singular vector  has an angular error
at most about
has an angular error
at most about

where
 is the relative gap between
is the relative gap between  and the nearest other singular
value. The same bound applies to the right singular vector
and the nearest other singular
value. The same bound applies to the right singular vector  and
and  .
Since the relative gap
may be much larger than
the absolute gap
,
this error bound may be much smaller than the previous one. The relative gaps
may be easily computed from the array of computed singular values.
.
Since the relative gap
may be much larger than
the absolute gap
,
this error bound may be much smaller than the previous one. The relative gaps
may be easily computed from the array of computed singular values.
In the very special case of 2-by-2 bidiagonal matrices, xBDSQR
calls auxiliary routine xLASV2 to compute the SVD. xLASV2 will
actually compute nearly correctly rounded singular vectors independent of
the relative gap, but this requires accurate computer arithmetic:
if leading digits cancel during floating-point subtraction, the resulting
difference must be exact.
On machines without guard digits one has the slightly weaker result that the
algorithm is componentwise relatively backward stable, and therefore the
accuracy
of the singular vectors depends on the relative gap as described
above.
Jacobi's method
[69]
[76]
[24] is another
algorithm for finding singular values and singular vectors of matrices.
It is slower than the algorithms based on first tridiagonalizing the matrix,
but is capable of computing more accurate answers in several important cases.
Routines implementing Jacobi's method and corresponding error bounds will be
available in a future LAPACK release.





Next:
Error Bounds for
Up:
Error Bounds for
Previous:
Error Bounds for
Tue Nov 29 14:03:33 EST 1994
Error Bounds for the Generalized Symmetric Definite
Eigenproblem





Next:
Further Details: Error
Up:
Accuracy and Stability
Previous:
Further Details: Error
There are three types of problems to consider.
In all cases A and B
are real symmetric (or complex Hermitian) and B is positive definite.
These decompositions are computed for real symmetric matrices
by the driver routines
xSYGV, xSPGV and (for type 1 only) xSBGV (see subsection
2.2.5.1).
These decompositions are computed for complex Hermitian matrices
by the driver routines
xHEGV, xHPGV and (for type 1 only) xHBGV (see subsection
2.2.5.1).
In each of the following three decompositions,
 is real and diagonal with diagonal entries
is real and diagonal with diagonal entries
 , and
the columns
, and
the columns  of Z are linearly independent vectors.
The
of Z are linearly independent vectors.
The  are called
eigenvalues and the
are called
eigenvalues and the  are
eigenvectors.
are
eigenvectors.
-
 .
The eigendecomposition may be written
.
The eigendecomposition may be written  and
and
 (or
(or  and
and  if A and B are complex).
This may also be written
if A and B are complex).
This may also be written  .
.
-
 .
The eigendecomposition may be written
.
The eigendecomposition may be written  and
and
 (
( and
and  if A
and B are complex).
This may also be written
if A
and B are complex).
This may also be written  .
.
-
 .
The eigendecomposition may be written
.
The eigendecomposition may be written  and
and  (
( and
and  if A
and B are complex).
This may also be written
if A
and B are complex).
This may also be written  .
.
The approximate error bounds
for the computed eigenvalues  are
are

The approximate error
bounds
for the computed eigenvectors  ,
which bound the acute angles between the computed eigenvectors and true
eigenvectors
,
which bound the acute angles between the computed eigenvectors and true
eigenvectors  , are
, are

These bounds are computed differently, depending on which of the above three
problems are to be solved. The following code fragments show how.
-
First we consider error bounds for problem 1.
EPSMCH = SLAMCH( 'E' )
* Solve the eigenproblem A - lambda B (ITYPE = 1)
ITYPE = 1
* Compute the norms of A and B
ANORM = SLANSY( '1', UPLO, N, A, LDA, WORK )
BNORM = SLANSY( '1', UPLO, N, B, LDB, WORK )
* The eigenvalues are returned in W
* The eigenvectors are returned in A
CALL SSYGV( ITYPE, 'V', UPLO, N, A, LDA, B, LDB, W,
$ WORK, LWORK, INFO )
IF( INFO.GT.0 .AND. INFO.LE.N ) THEN
PRINT *,'SSYGV did not converge'
ELSE IF( INFO.GT.N ) THEN
PRINT *,'B not positive definite'
ELSE IF ( N.GT.0 ) THEN
* Get reciprocal condition number RCONDB of Cholesky
* factor of B
CALL STRCON( '1', UPLO, 'N', N, B, LDB, RCONDB,
$ WORK, IWORK, INFO )
RCONDB = MAX( RCONDB, EPSMCH )
CALL SDISNA( 'Eigenvectors', N, N, W, RCONDZ, INFO )
DO 10 I = 1, N
EERRBD( I ) = ( EPSMCH / RCONDB**2 ) *
$ ( ANORM / BNORM + ABS( W(I) ) )
ZERRBD( I ) = ( EPSMCH / RCONDB**3 ) *
$ ( ( ANORM / BNORM ) / RCONDZ(I) +
$ ( ABS( W(I) ) / RCONDZ(I) ) * RCONDB )
10 CONTINUE
END IF
For example, if
 ,
,

then ANORM = 120231,
BNORM = 120, and
RCOND = .8326, and
the approximate eigenvalues, approximate error bounds,
and true errors are

This code fragment cannot be adapted to use xSBGV (or xHBGV),
because xSBGV does not return a conventional Cholesky factor in B,
but rather a ``split'' Choleksy factorization (performed by xPBSTF).
A future LAPACK release will include error bounds for xSBGV.
-
Problem types 2 and 3 have the same error bounds. We illustrate
only type 2.
EPSMCH = SLAMCH( 'E' )
* Solve the eigenproblem A*B - lambda I (ITYPE = 2)
ITYPE = 2
* Compute the norms of A and B
ANORM = SLANSY( '1', UPLO, N, A, LDA, WORK )
BNORM = SLANSY( '1', UPLO, N, B, LDB, WORK )
* The eigenvalues are returned in W
* The eigenvectors are returned in A
CALL SSYGV( ITYPE, 'V', UPLO, N, A, LDA, B, LDB, W,
$ WORK, LWORK, INFO )
IF( INFO.GT.0 .AND. INFO.LE.N ) THEN
PRINT *,'SSYGV did not converge'
ELSE IF( INFO.GT.N ) THEN
PRINT *,'B not positive definite'
ELSE IF ( N.GT.0 ) THEN
* Get reciprocal condition number RCONDB of Cholesky
* factor of B
CALL STRCON( '1', UPLO, 'N', N, B, LDB, RCONDB,
$ WORK, IWORK, INFO )
RCONDB = MAX( RCONDB, EPSMCH )
CALL SDISNA( 'Eigenvectors', N, N, W, RCONDZ, INFO )
DO 10 I = 1, N
EERRBD(I) = ( ANORM * BNORM ) * EPSMCH +
$ ( EPSMCH / RCONDB**2 ) * ABS( W(I) )
ZERRBD(I) = ( EPSMCH / RCONDB ) * ( ( ANORM *
$ BNORM ) / RCONDZ(I) + 1.0 / RCONDB )
10 CONTINUE
END IF
For the same A and B as above, the approximate eigenvalues,
approximate error bounds, and true errors are






Next:
Further Details: Error
Up:
Accuracy and Stability
Previous:
Further Details: Error
Tue Nov 29 14:03:33 EST 1994
Further Details: Error Bounds for the Generalized Symmetric Definite
Eigenproblem





Next:
Error Bounds for
Up:
Error Bounds for
Previous:
Error Bounds for
The error analysis of the driver routine xSYGV, or xHEGV in the complex case
(see subsection
2.2.5.1),
goes as follows.
In all cases
 is
the absolute gap
between
is
the absolute gap
between  and the nearest other eigenvalue.
and the nearest other eigenvalue.
-
 .
The computed eigenvalues
.
The computed eigenvalues  can differ
from true eigenvalues
can differ
from true eigenvalues  by at most about
by at most about
The angular difference between the computed eigenvector
 and a true eigenvector
and a true eigenvector  is
is

-
 or
or  .
The computed eigenvalues
.
The computed eigenvalues  can differ
from true eigenvalues
can differ
from true eigenvalues  by at most about
by at most about
The angular difference between the computed eigenvector
 and a true eigenvector
and a true eigenvector  is
is

The code fragments above replace p(n) by 1, and makes sure
neither RCONDB nor RCONDZ is so small as to cause
overflow when used as divisors in the expressions for error bounds.
These error bounds are large when B is ill-conditioned with respect to
inversion ( is large). It is often the case that the eigenvalues
and eigenvectors are much better conditioned than indicated here.
We mention three ways to get tighter bounds.
The first way is effective when the diagonal entries of B differ
widely in magnitude
is large). It is often the case that the eigenvalues
and eigenvectors are much better conditioned than indicated here.
We mention three ways to get tighter bounds.
The first way is effective when the diagonal entries of B differ
widely in magnitude
 :
:
-
 . Let
. Let  be a diagonal matrix.
Then replace B by DBD and A by DAD in the above bounds.
be a diagonal matrix.
Then replace B by DBD and A by DAD in the above bounds.
-
 or
or  .
Let
.
Let  be a diagonal matrix.
Then replace B by DBD and A by
be a diagonal matrix.
Then replace B by DBD and A by  in the above bounds.
in the above bounds.
The second way to get tighter bounds does not actually supply guaranteed
bounds, but its estimates are often better in practice.
It is not guaranteed because it assumes the algorithm is backward stable,
which is not necessarily true when B is ill-conditioned.
It estimates the chordal distance between a
true eigenvalue  and a computed eigenvalue
and a computed eigenvalue  :
:

To interpret this measure we write  and
and  . Then
. Then
 .
In other words, if
.
In other words, if  represents the one-dimensional subspace
represents the one-dimensional subspace
 consisting of the line through the origin with slope
consisting of the line through the origin with slope  ,
and
,
and  represents the analogous subspace S, then
represents the analogous subspace S, then
 is the sine of the acute angle
is the sine of the acute angle  between these
subspaces.
Thus X is bounded by one, and is small when both arguments are
large
between these
subspaces.
Thus X is bounded by one, and is small when both arguments are
large
 .
It applies only to the first problem,
.
It applies only to the first problem,  :
:
Suppose a computed eigenvalue  of
of  is
the exact eigenvalue of a perturbed problem
is
the exact eigenvalue of a perturbed problem  .
Let
.
Let  be the unit eigenvector (
be the unit eigenvector ( ) for the exact
eigenvalue
) for the exact
eigenvalue  .
Then if ||E|| is small compared to
|A|, and if ||F|| is small compared to ||B||, we have
.
Then if ||E|| is small compared to
|A|, and if ||F|| is small compared to ||B||, we have
Thus  is a condition number for
eigenvalue
is a condition number for
eigenvalue  .
.
The third way applies only to the first problem  , and only
when A is positive definite. We use a different algorithm:
, and only
when A is positive definite. We use a different algorithm:
- Compute the Cholesky factorization of
 , using xPOTRF.
, using xPOTRF.
- Compute the Cholesky factorization of
 , using xPOTRF.
, using xPOTRF.
- Compute the generalized singular value decomposition of the pair
 ,
,  using xTGSJA. The squares of the generalized singular
values are the desired eigenvalues.
using xTGSJA. The squares of the generalized singular
values are the desired eigenvalues.
See sections
2.2.5.3 and
2.3.9
for a discussion of the generalized singular
value decomposition, and section
4.12 for a discussion of
the relevant error bound. This approach can give a tighter error bound
than the above bounds when B is ill conditioned but A + B is
well-conditioned.
Other yet more refined algorithms and error bounds are discussed in
[78]
[73]
[13], and will be available in
future releases.





Next:
Error Bounds for
Up:
Error Bounds for
Previous:
Error Bounds for
Tue Nov 29 14:03:33 EST 1994
Error Bounds for the Generalized Nonsymmetric Eigenproblem





Next:
Error Bounds for
Up:
Accuracy and Stability
Previous:
Further Details: Error
The generalized nonsymmetric eigenproblem is discussed in
section
2.2.5.2,
and has error bounds which are analogous to those
for the nonsymmetric eigenvalue problem presented in section
4.8. These
bounds will be computed by future LAPACK routines xGGEVX and xGGESX, and discussed in
a future version of this manual.
Tue Nov 29 14:03:33 EST 1994
Error Bounds for the Generalized Singular Value Decomposition





Next:
Further Details: Error
Up:
Accuracy and Stability
Previous:
Error Bounds for
The generalized (or quotient) singular value decomposition
of an m-by-n matrix
A and a p-by-n matrix B is the pair of factorizations

where V, V, Q, R,  and
and  are defined
as follows.
are defined
as follows.
- U is m-by-m, V is p-by-p, Q is n-by-n,
and all three matrices are orthogonal. If A and
B are complex, these matrices are unitary instead
of orthogonal, and
 should be
replaced by
should be
replaced by  in the pair of factorizations.
in the pair of factorizations.
- R is r-by-r, upper triangular and nonsingular.
[0 , R] is r-by-n. The integer r is the rank of
 , and satisfies r > = n.
, and satisfies r > = n.
-
 is m-by-r,
is m-by-r,
 is p-by-r, both are real, nonnegative and diagonal,
and
is p-by-r, both are real, nonnegative and diagonal,
and  .
Write
.
Write
 and
and
 ,
where
,
where  and
and  lie in the interval from 0 to 1.
The ratios
lie in the interval from 0 to 1.
The ratios
 are called the generalized singular values of the pair A , B.
If
are called the generalized singular values of the pair A , B.
If  , then the generalized singular value
, then the generalized singular value
 is infinite.
For details on the structure of
is infinite.
For details on the structure of  ,
,  and R, see
section
2.2.5.3.
and R, see
section
2.2.5.3.
The generalized singular value decomposition is
computed by driver routine xGGSVD (see section
2.2.5.3).
We will give error bounds for the generalized
singular values in the
common case where  has full
rank r = n.
Let
has full
rank r = n.
Let  and
and  be the values of
be the values of  and
and  , respectively,
computed by xGGSVD.
The approximate error
bound
for these values is
, respectively,
computed by xGGSVD.
The approximate error
bound
for these values is

Note that if  is close to zero, then a true
generalized singular value
is close to zero, then a true
generalized singular value
 can differ greatly in magnitude from
the computed generalized singular value
can differ greatly in magnitude from
the computed generalized singular value
 , even if SERRBD is
close to its minimum
, even if SERRBD is
close to its minimum  .
.
Here is another way to interpret SERRBD:
if we think of  and
and  as representing the subspace S
consisting of the straight line through the origin with slope
as representing the subspace S
consisting of the straight line through the origin with slope
 , and similarly
, and similarly  and
and  representing the subspace
representing the subspace  ,
then SERRBD bounds the acute angle between
S and
,
then SERRBD bounds the acute angle between
S and  .
Note that any two
lines through the origin with nearly vertical slopes
(very large
.
Note that any two
lines through the origin with nearly vertical slopes
(very large  ) are close together in angle.
(This is related to the chordal distance in
section
4.10.1.)
) are close together in angle.
(This is related to the chordal distance in
section
4.10.1.)
SERRBD can be computed by the following code fragment,
which for simplicity assumes m > = n.
(The assumption r = n implies only that p + m > = n.
Error bounds can also be computed when p + m > = n > m,
with slightly more complicated code.)
EPSMCH = SLAMCH( 'E' )
* Compute generalized singular values of A and B
CALL SGGSVD( 'N', 'N', 'N', M, N, P, K, L, A, LDA, B,
$ LDB, ALPHA, BETA, U, LDU, V, LDV, Q, LDQ,
$ WORK, IWORK, INFO )
* Compute rank of [A',B']'
RANK = K+L
IF( INFO.GT.0 ) THEN
PRINT *,'SGGSVD did not converge'
ELSE IF( RANK.LT.N ) THEN
PRINT *,'[A**T,B**T]**T not full rank'
ELSE IF ( M .GE. N .AND. N .GT. 0 ) THEN
* Compute reciprocal condition number RCOND of R
CALL STRCON( 'I', 'U', 'N', N, A, LDA, RCOND, WORK,
$ IWORK, INFO )
RCOND = MAX( RCOND, EPSMCH )
SERRBD = EPSMCH / RCOND
END IF
For example, if
 ,
,

then, to 4 decimal places,

 , and the true errors
are
, and the true errors
are  ,
,  and
and  .
.





Next:
Further Details: Error
Up:
Accuracy and Stability
Previous:
Error Bounds for
Tue Nov 29 14:03:33 EST 1994
Further Details: Error Bounds for the Generalized Singular Value Decomposition





Next:
Error Bounds for
Up:
Error Bounds for
Previous:
Error Bounds for
The GSVD algorithm used in LAPACK (
[12]
[10]
[62])
is backward stable:
Let the computed GSVD of A and B be  and
and
 .
This is nearly the exact GSVD of
A + E and B + F in the following sense. E and F are small:
.
This is nearly the exact GSVD of
A + E and B + F in the following sense. E and F are small:
there exist small
 ,
,  , and
, and  such that
such that
 ,
,
 , and
, and
 are exactly orthogonal (or unitary):
are exactly orthogonal (or unitary):

and

is the exact GSVD of A + E and B + F. Here p(n) is a modestly growing function of n, and
we take p(n) = 1 in the above code fragment.
Let  and
and  be the square roots of the diagonal entries of the exact
be the square roots of the diagonal entries of the exact
 and
and  ,
and let
,
and let  and
and  the square roots of the diagonal entries
of the computed
the square roots of the diagonal entries
of the computed  and
and  .
Let
.
Let

Then provided G and  have full rank n, one can show
[61]
[74] that
have full rank n, one can show
[61]
[74] that

In the code fragment we approximate the numerator of the last expression by
 and approximate the denominator by
and approximate the denominator by
 in order to compute SERRBD;
STRCON returns an approximation RCOND to
in order to compute SERRBD;
STRCON returns an approximation RCOND to
 .
.
We assume that the rank r of G equals n, because otherwise the
 s and
s and  s are not well determined. For example, if
s are not well determined. For example, if

then A and B have
 and
and  , whereas
, whereas
 and
and  have
have
 and
and  , which
are completely different, even though
, which
are completely different, even though  and
and
 . In this case,
. In this case,  ,
so G is nearly rank-deficient.
,
so G is nearly rank-deficient.
The reason the code fragment assumes m > = n is that in this case  is
stored overwritten on A, and can be passed to STRCON in order to compute
RCOND. If m < = n, then the
first m rows of
is
stored overwritten on A, and can be passed to STRCON in order to compute
RCOND. If m < = n, then the
first m rows of  are
stored in A, and the last m - n rows of
are
stored in A, and the last m - n rows of  are stored in B. This
complicates the computation of RCOND: either
are stored in B. This
complicates the computation of RCOND: either  must be copied to
a single array before calling STRCON, or else the lower level subroutine SLACON
must be used with code capable of solving linear equations with
must be copied to
a single array before calling STRCON, or else the lower level subroutine SLACON
must be used with code capable of solving linear equations with  and
and  as coefficient matrices.
as coefficient matrices.





Next:
Error Bounds for
Up:
Error Bounds for
Previous:
Error Bounds for
Tue Nov 29 14:03:33 EST 1994
Error Bounds for Fast Level 3 BLAS





Next:
Documentation and Software
Up:
Accuracy and Stability
Previous:
Further Details: Error
The Level 3 BLAS specifications
[28] specify the input, output
and calling sequence for each routine, but allow freedom of
implementation, subject to the requirement that the routines be
numerically stable
.
Level 3 BLAS implementations can therefore be
built using matrix multiplication algorithms that achieve a more
favorable operation count (for suitable dimensions) than the standard
multiplication technique, provided that these ``fast'' algorithms are
numerically stable. The simplest fast matrix multiplication
technique is Strassen's
method
, which can
multiply two n-by-n
matrices in fewer than  operations, where
operations, where
 .
.
The effect on the results in this chapter of using a fast Level 3 BLAS
implementation can be explained as follows. In general, reasonably
implemented fast Level 3 BLAS preserve all the bounds presented here
(except those at the end of subsection
4.10), but the constant
p(n) may increase somewhat. Also, the iterative refinement
routine
xyyRFS may take more steps to converge.
This is what we mean by reasonably implemented fast Level 3 BLAS.
Here,  denotes a constant depending on the specified matrix dimensions.
denotes a constant depending on the specified matrix dimensions.
(1) If A is m-by-n, B is n-by-p and  is the computed
approximation to C = AB, then
is the computed
approximation to C = AB, then

(2)
The computed solution

to the triangular systems TX = B,
where T is m-by-m and B is m-by-p, satisfies

For conventional Level 3 BLAS implementations these conditions
hold with

and

.
Strassen's method
satisfies these
bounds for slightly larger

and

.
For further details, and references to fast multiplication techniques,
see
[20].
Tue Nov 29 14:03:33 EST 1994
Documentation and Software Conventions





Next:
Design and Documentation
Up:
Guide
Previous:
Error Bounds for
Tue Nov 29 14:03:33 EST 1994
Contents




Next:
List of
Up:
LAPACK Users' Guide
Release 2.0
Previous:
LAPACK Users' Guide
Release 2.0
Tue Nov 29 14:03:33 EST 1994
Contents




Next:
List of
Up:
LAPACK Users' Guide
Release 2.0
Previous:
LAPACK Users' Guide
Release 2.0
Tue Nov 29 14:03:33 EST 1994
LAPACK Users' Guide <BR>Release 2.0





Next:
Contents
LAPACK Users' Guide
Release 2.0
E. Anderson,
Z. Bai,
C. Bischof,
J. Demmel,
J. Dongarra,
J. Du Croz,
A. Greenbaum,
S. Hammarling,
A. McKenney,
S. Ostrouchov,
D. Sorensen
30 September 1994
This work is dedicated to Jim Wilkinson whose ideas and
spirit have given us inspiration and influenced the project
at every turn.
Tue Nov 29 14:03:33 EST 1994
Band Storage





Next:
Tridiagonal and Bidiagonal
Up:
Matrix Storage Schemes
Previous:
Packed Storage
An  -by-
-by- band matrix
with
band matrix
with  subdiagonals
and
subdiagonals
and  superdiagonals may be
stored compactly in a two-dimensional array with
superdiagonals may be
stored compactly in a two-dimensional array with  rows and
rows and  columns.
Columns of the matrix are stored in corresponding columns of the
array, and diagonals of the matrix are stored in rows of the array.
This storage scheme should be used in practice only if
columns.
Columns of the matrix are stored in corresponding columns of the
array, and diagonals of the matrix are stored in rows of the array.
This storage scheme should be used in practice only if  ,
although LAPACK routines work correctly for all values of
,
although LAPACK routines work correctly for all values of  and
and  .
In LAPACK, arrays that hold matrices in band storage have names
ending in `B'.
.
In LAPACK, arrays that hold matrices in band storage have names
ending in `B'.
To be precise,  is stored in AB(
is stored in AB( ) for
) for
 .
For example, when
.
For example, when  ,
,  and
and  :
:

The elements marked  in the upper left and lower right
corners of the array AB need not be set, and are not referenced by
LAPACK routines.
in the upper left and lower right
corners of the array AB need not be set, and are not referenced by
LAPACK routines.
Note: when a band matrix is supplied for  factorization,
space
must be allowed to store an
additional
factorization,
space
must be allowed to store an
additional  superdiagonals,
generated by fill-in as a result of row interchanges.
This means that the matrix is stored according to the above scheme,
but with
superdiagonals,
generated by fill-in as a result of row interchanges.
This means that the matrix is stored according to the above scheme,
but with  superdiagonals.
superdiagonals.
Triangular band matrices are stored in the same format, with either
 if upper triangular, or
if upper triangular, or  if
lower triangular.
if
lower triangular.
For symmetric or Hermitian band matrices with  subdiagonals or
superdiagonals, only the upper or lower triangle (as specified by
UPLO) need be stored:
subdiagonals or
superdiagonals, only the upper or lower triangle (as specified by
UPLO) need be stored:
For example, when  and
and  :
:

EISPACK
routines use a different storage scheme for band matrices,
in which rows of the matrix are stored in corresponding rows of the
array, and diagonals of the matrix are stored in columns of the array
(see Appendix
D).
Tue Nov 29 14:03:33 EST 1994
Tridiagonal and Bidiagonal Matrices





Next:
Unit Triangular Matrices
Up:
Matrix Storage Schemes
Previous:
Band Storage
An unsymmetric
tridiagonal matrix of order  is stored in
three one-dimensional arrays, one of length
is stored in
three one-dimensional arrays, one of length  containing the
diagonal elements, and two of length
containing the
diagonal elements, and two of length  containing the
subdiagonal and superdiagonal elements in elements
containing the
subdiagonal and superdiagonal elements in elements  .
.
A symmetric
tridiagonal or
bidiagonal
matrix is stored in
two one-dimensional arrays, one of length  containing the
diagonal elements, and one of length
containing the
diagonal elements, and one of length  containing the
off-diagonal elements. (EISPACK routines store the off-diagonal
elements in elements
containing the
off-diagonal elements. (EISPACK routines store the off-diagonal
elements in elements  of a vector of length
of a vector of length  .)
.)
Tue Nov 29 14:03:33 EST 1994
Generalized <IMG ALIGN=BOTTOM SRC="http://www.netlib.org/lapack/lug/_18064_tex2html_wrap12882.gif">
factorization





Next:
Symmetric Eigenproblems
Up:
Generalized Orthogonal Factorizations
Previous:
Generalized Factorization
The generalized  (GRQ) factorization of an
(GRQ) factorization of an  -by-
-by- matrix
matrix  and
a
and
a  -by-
-by- matrix
matrix  is given by the pair of factorizations
is given by the pair of factorizations

where  and
and  are respectively
are respectively  -by-
-by- and
and  -by-
-by- orthogonal
matrices (or unitary matrices if
orthogonal
matrices (or unitary matrices if  and
and  are complex).
are complex).
 has the form
has the form

or

where  or
or  is upper triangular.
is upper triangular.  has the form
has the form

or

where  is upper triangular.
is upper triangular.
Note that if  is square and nonsingular, the GRQ factorization of
is square and nonsingular, the GRQ factorization of
 and
and  implicitly gives the
implicitly gives the  factorization of the matrix
factorization of the matrix  :
:

without explicitly computing the matrix inverse  or the product
or the product
 .
.
The routine xGGRQF computes the GRQ factorization
by first computing the  factorization of
factorization of  and then
the
and then
the  factorization of
factorization of  .
The orthogonal (or unitary) matrices
.
The orthogonal (or unitary) matrices  and
and  can either be formed explicitly or
just used to multiply another given matrix in the same way as the
orthogonal (or unitary) matrix
in the
can either be formed explicitly or
just used to multiply another given matrix in the same way as the
orthogonal (or unitary) matrix
in the  factorization
(see section
2.3.2).
factorization
(see section
2.3.2).
The GRQ factorization can be used to solve the linear
equality-constrained least squares problem (LSE) (see (
2.2) and
[page 567]GVL2).
We use the GRQ factorization of  and
and  (note that
(note that  and
and  have
swapped roles), written as
have
swapped roles), written as

We write the linear equality constraints  as:
as:

which we partition as:

Therefore  is the solution of the upper triangular system
is the solution of the upper triangular system

Furthermore,

We partition this expression as:

where  , which
can be computed by xORMQR (or xUNMQR).
, which
can be computed by xORMQR (or xUNMQR).
To solve the LSE problem, we set

which gives  as the solution of the upper triangular system
as the solution of the upper triangular system

Finally, the desired solution is given by

which can be computed
by xORMRQ (or xUNMRQ).
Tue Nov 29 14:03:33 EST 1994
 diagonal entries
of
diagonal entries
of  and
and  , we would get 0/0. For a detailed
mathematical discussion of this decomposition, see the discussion of
the Kronecker Canonical Form in
[43].
, we would get 0/0. For a detailed
mathematical discussion of this decomposition, see the discussion of
the Kronecker Canonical Form in
[43]. , we may add some zero rows to
, we may add some zero rows to  to make
it upper triangular.
to make
it upper triangular. where both
where both
 and
and  are small. This does not significantly change the following
analysis.
are small. This does not significantly change the following
analysis. , and may use the Lipschitz
constant in place of
, and may use the Lipschitz
constant in place of  in deriving error bounds.
in deriving error bounds. to be continuous,
whereas we require Lipschitz continuity.
to be continuous,
whereas we require Lipschitz continuity. is small taking the
columns of the computed inverse one at
a time, with a different
is small taking the
columns of the computed inverse one at
a time, with a different  for each column
[38].
The same is true when computing
the eigenvectors of a nonsymmetric matrix.
When computing the eigenvalues and eigenvectors
of
for each column
[38].
The same is true when computing
the eigenvectors of a nonsymmetric matrix.
When computing the eigenvalues and eigenvectors
of  ,
,  or
or  ,
with
,
with  symmetric and
symmetric and  symmetric and positive definite
(using xSYGV or xHEGV) then the method may not be backward normwise stable if
symmetric and positive definite
(using xSYGV or xHEGV) then the method may not be backward normwise stable if
 has a large condition number
has a large condition number  ,
although it has useful error bounds in this case too
(see section
4.10). Solving the Sylvester equation
,
although it has useful error bounds in this case too
(see section
4.10). Solving the Sylvester equation
 for the matrix
for the matrix  may not be backward stable, although
there are again useful error bounds for
may not be backward stable, although
there are again useful error bounds for  [54].
[54]. which is a modestly growing function of the problem dimension
which is a modestly growing function of the problem dimension  .
Often
.
Often  .
. and
and  . With nonsymmetric matrices
. With nonsymmetric matrices
 is usually just the computed eigenvalue closest to
is usually just the computed eigenvalue closest to
 , but in very ill-conditioned problems this is not always true.
In the most general case, the one-to-one correspondence may be described
in the following nonconstructive way: Let
, but in very ill-conditioned problems this is not always true.
In the most general case, the one-to-one correspondence may be described
in the following nonconstructive way: Let  be the eigenvalues
of
be the eigenvalues
of  and
and  be the eigenvalues of
be the eigenvalues of  . Let
. Let
 be the eigenvalues of
be the eigenvalues of  , where
, where  is a parameter,
which is initially zero, so that we may set
is a parameter,
which is initially zero, so that we may set  .
As
.
As  increase from 0 to 1,
increase from 0 to 1,  traces out a curve from
traces out a curve from
 to
to  , providing the correspondence.
Care must be taken when the curves intersect, and the correspondence
may not be unique.
, providing the correspondence.
Care must be taken when the curves intersect, and the correspondence
may not be unique. are simply related to the eigenvalues and eigenvectors of
the Hermitian matrix
are simply related to the eigenvalues and eigenvectors of
the Hermitian matrix  [p. 427]GVL2.
[p. 427]GVL2. and
and
 on the Riemann sphere, i.e., half the length of the chord
connecting the projections.
on the Riemann sphere, i.e., half the length of the chord
connecting the projections. max(1,N)''
rather than simply
``LDA
max(1,N)''
rather than simply
``LDA  N'' because LDA must always be at least 1, even if N = 0,
to satisfy the
requirements of standard Fortran; on some systems,
a zero or negative value of LDA would cause a run-time fault.
N'' because LDA must always be at least 1, even if N = 0,
to satisfy the
requirements of standard Fortran; on some systems,
a zero or negative value of LDA would cause a run-time fault.
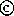 1994 by the
Society for Industrial and Applied Mathematics. Certain derivative work
portions have been copyrighted by the Numerical Algorithms Group Ltd.
1994 by the
Society for Industrial and Applied Mathematics. Certain derivative work
portions have been copyrighted by the Numerical Algorithms Group Ltd.
 , then X(i) holds
, then X(i) holds  for
for
 for i = 1,..., m and
j = 1,..., n (LDA must be at least m).
See Section
for i = 1,..., m and
j = 1,..., n (LDA must be at least m).
See Section  indicates an array element that need not be set
and is not referenced by LAPACK routines. Elements that ``need not be
set'' are never read, written to, or otherwise accessed by the LAPACK
routines. The examples illustrate only the
relevant part of the arrays; array arguments may of course have additional
rows or columns, according to the usual rules for passing array arguments
in Fortran 77.
indicates an array element that need not be set
and is not referenced by LAPACK routines. Elements that ``need not be
set'' are never read, written to, or otherwise accessed by the LAPACK
routines. The examples illustrate only the
relevant part of the arrays; array arguments may of course have additional
rows or columns, according to the usual rules for passing array arguments
in Fortran 77.





 ). For example,
). For example,
 without forming Q explicitly.
without forming Q explicitly.

 is a scalar, and v is an n-vector, with
is a scalar, and v is an n-vector, with
 ); v is often referred to
as the Householder vector
); v is often referred to
as the Householder vector ; hence
; hence  need not
be stored. In real arithmetic,
need not
be stored. In real arithmetic,  , except that
, except that
 implies H = I.
implies H = I.
 and
and  .
Thus a complex H is
not Hermitian (as it is in other representations), but it is unitary,
which is the important property. The advantage of allowing
.
Thus a complex H is
not Hermitian (as it is in other representations), but it is unitary,
which is the important property. The advantage of allowing 
 . This is useful, for example,
when reducing a complex Hermitian matrix to real symmetric tridiagonal form
. This is useful, for example,
when reducing a complex Hermitian matrix to real symmetric tridiagonal form

 is equivalent
to
is equivalent
to  .
(The same convention is used in Part
.
(The same convention is used in Part 



















 . For example, the EISPACK routine ELMHES uses non-orthogonal
transformations, whereas the nearest equivalent LAPACK routine, SGEHRD, uses
orthogonal transformations.
. For example, the EISPACK routine ELMHES uses non-orthogonal
transformations, whereas the nearest equivalent LAPACK routine, SGEHRD, uses
orthogonal transformations.

 .
.




 Factorization with Efficient
Pipelining and Overlap on a Multiprocessor,
UT, CS-93-218, December, 1993.
Factorization with Efficient
Pipelining and Overlap on a Multiprocessor,
UT, CS-93-218, December, 1993.
 , SIAM J. Num. Anal., 9 (1972), pp. 669-686.
, SIAM J. Num. Anal., 9 (1972), pp. 669-686.
 Writing index file .idxK
Writing index file .idxK 
 Writing index file .idxR
Writing index file .idxR 
 factorization
factorization N double-words of memory,
stored in column-major order: elements in a column are
contiguous, and elements within a row are separated by a stride of LDA
double-words.
N double-words of memory,
stored in column-major order: elements in a column are
contiguous, and elements within a row are separated by a stride of LDA
double-words.
 has the value
has the value 
 or
or  (unless A is symmetric or Hermitian);
(unless A is symmetric or Hermitian);

 ,
and the problem
is referred to as finding a minimum norm solution
,
and the problem
is referred to as finding a minimum norm solution .
.
 .
.

 has full column rank n.
Under these assumptions, the problem LSE
has full column rank n.
Under these assumptions, the problem LSE

 , and corresponding eigenvectors
, and corresponding eigenvectors , such that
, such that


 is a diagonal matrix whose diagonal elements are the
eigenvalues
is a diagonal matrix whose diagonal elements are the
eigenvalues , such that
, such that
 satisfying
satisfying



 is an m-by-n diagonal matrix with real
diagonal elements,
is an m-by-n diagonal matrix with real
diagonal elements,  , such that
, such that

 and
and  are the i-th columns of U and V respectively.
are the i-th columns of U and V respectively.



 (problem types 1 and 3) or
(problem types 1 and 3) or  (problem type 2), where
(problem type 2), where  (problem types 1 and 2) or
(problem types 1 and 2) or  (problem type 3).
(problem type 3).
 such that
such that
 and corresponding eigenvectors
and corresponding eigenvectors
 such that
such that
 and
and  if neither
if neither  and
and  and
and  .
.
 are called right eigenvectors. Vectors
are called right eigenvectors. Vectors
 satisfying
satisfying
 (in the presence of roundoff,
(in the presence of roundoff,  and
and  and
and 


 should be
replaced by
should be
replaced by  , and satisfies r < = n.
, and satisfies r < = n.
 is m-by-r,
is m-by-r,
 is p-by-r, both are real, nonnegative and diagonal, and
is p-by-r, both are real, nonnegative and diagonal, and
 .
Write
.
Write
 and
and
 ,
where
,
where  and
and  lie in the interval from 0 to 1.
The ratios
lie in the interval from 0 to 1.
The ratios
 are called the generalized singular values of the pair A,B,
are called the generalized singular values of the pair A,B,  , then the generalized singular value
, then the generalized singular value
 is infinite.
is infinite.

 , and S is nonsingular.
We may also identify
, and S is nonsingular.
We may also identify
 ,
,
 for
for  ,
,
 , and
, and
 for
for  are infinite, and the remaining l generalized singular values
are finite.
are infinite, and the remaining l generalized singular values
are finite.


 ,
,
 for
for  ,
,
 ,
,
 .
Thus, the first
.
Thus, the first  generalized singular values
generalized singular values
 are infinite, and the remaining
are infinite, and the remaining  generalized singular values
are finite.
generalized singular values
are finite.
 , where the singular
values of
, where the singular
values of 
 are orthonormal, then r = n, R = I and the
generalized
singular value decomposition of A and B is equivalent to the CS
(Cosine-Sine) decomposition of
are orthonormal, then r = n, R = I and the
generalized
singular value decomposition of A and B is equivalent to the CS
(Cosine-Sine) decomposition of 
 can be expressed in terms of the generalized singular value decomposition:
Let
can be expressed in terms of the generalized singular value decomposition:
Let

 and
and  .
.


 factorization):
factorization):



 ;
Higham's modification
;
Higham's modification  ,
except for symmetric positive definite tridiagonal matrices for which it
is computed directly with comparable efficiency
,
except for symmetric positive definite tridiagonal matrices for which it
is computed directly with comparable efficiency  (not provided for band matrices, because the inverse
does not in general preserve bandedness);
(not provided for band matrices, because the inverse
does not in general preserve bandedness);

 ;
a complex matrix Q is unitary if
;
a complex matrix Q is unitary if  .
Orthogonal or unitary matrices have the important property that they leave the
two-norm of a vector invariant:
.
Orthogonal or unitary matrices have the important property that they leave the
two-norm of a vector invariant:



 consists of the first n columns of Q, and
consists of the first n columns of Q, and  the
remaining m - n columns.
the
remaining m - n columns.

 is upper triangular and
is upper triangular and  is rectangular.
is rectangular.

 consists of its first
n elements. Then
x is the solution of the upper triangular system
consists of its first
n elements. Then
x is the solution of the upper triangular system

 may be computed without forming r
explicitly, since
may be computed without forming r
explicitly, since






 in rows and columns k + 1 to n
would be zero. In numerical computation, the aim must be to
determine an index k, such that the leading submatrix
in rows and columns k + 1 to n
would be zero. In numerical computation, the aim must be to
determine an index k, such that the leading submatrix  in the first
k rows and columns is well-conditioned, and
in the first
k rows and columns is well-conditioned, and 

 consists of just the first k elements of
consists of just the first k elements of  .
.
 . However,
by applying further orthogonal (or unitary) transformations
. However,
by applying further orthogonal (or unitary) transformations ,
using the routine xTZRQF,
,
using the routine xTZRQF,  can be eliminated:
can be eliminated:









 or
or  is upper triangular.
is upper triangular.
 :
:
 or the product
or the product  .
The orthogonal (or unitary) matrices Q and Z
can either be formed explicitly or just used to multiply another given matrix
in the same way as the
orthogonal (or unitary) matrix in the QR factorization
(see section
.
The orthogonal (or unitary) matrices Q and Z
can either be formed explicitly or just used to multiply another given matrix
in the same way as the
orthogonal (or unitary) matrix in the QR factorization
(see section 


 can be computed by xORMQR (or xUNMQR).
can be computed by xORMQR (or xUNMQR).



 is upper triangular. T has the form
is upper triangular. T has the form

 is upper triangular.
is upper triangular.

 .
The orthogonal (or unitary) matrices Q and Z
can either be formed explicitly or
just used to multiply another given matrix in the same way as the
orthogonal (or unitary) matrix
in the RQ factorization
(see section
.
The orthogonal (or unitary) matrices Q and Z
can either be formed explicitly or
just used to multiply another given matrix in the same way as the
orthogonal (or unitary) matrix
in the RQ factorization
(see section 
 is the solution of the upper triangular system
is the solution of the upper triangular system 


 , which
can be computed by xORMQR (or xUNMQR).
, which
can be computed by xORMQR (or xUNMQR).
 as the solution of the upper triangular system
as the solution of the upper triangular system

 .
.  with Q orthogonal
and T symmetric tridiagonal.
If A is complex Hermitian, the
decomposition is
with Q orthogonal
and T symmetric tridiagonal.
If A is complex Hermitian, the
decomposition is  with Q unitary and T, as before,
real symmetric tridiagonal
with Q unitary and T, as before,
real symmetric tridiagonal , where S is orthogonal and
, where S is orthogonal and  (
( when
A is complex Hermitian).
when
A is complex Hermitian).
 or
or  ).
See
).
See  . A nonzero column vector u
satisfying
. A nonzero column vector u
satisfying  is called the left eigenvector
is called the left eigenvector , where
Z is unitary and T is upper triangular. If A is real, its
Schur factorization is
, where
Z is unitary and T is upper triangular. If A is real, its
Schur factorization is  , where Z is orthogonal.
and T is upper quasi-triangular (1-by-1 and 2-by-2 blocks on
its diagonal).
The columns of Z are called the Schur vectors of A.
, where Z is orthogonal.
and T is upper quasi-triangular (1-by-1 and 2-by-2 blocks on
its diagonal).
The columns of Z are called the Schur vectors of A.
 with Q orthogonal if A is real, or
with Q orthogonal if A is real, or
 with Q unitary if A is complex.
The reduction is performed by subroutine xGEHRD, which
represents
with Q unitary if A is complex.
The reduction is performed by subroutine xGEHRD, which
represents
 (for H real) or
(for H real) or  (for H complex). The matrix A (the Schur vectors
of H) may
optionally be computed as well. Alternatively S may be postmultiplied
into the matrix Q determined in stage 1, to give the matrix Z = QS, the
Schur vectors of A. The eigenvalues
(for H complex). The matrix A (the Schur vectors
of H) may
optionally be computed as well. Alternatively S may be postmultiplied
into the matrix Q determined in stage 1, to give the matrix Z = QS, the
Schur vectors of A. The eigenvalues
 and
and  are
upper triangular.
Thus the matrix is already in Schur form
are
upper triangular.
Thus the matrix is already in Schur form in rows and columns ILO to IHI.
in rows and columns ILO to IHI.
 to make the rows and columns of
to make the rows and columns of 
 ;
xGEBAK
;
xGEBAK ,
,  for A, given
matrices A, B and C, with A and B (quasi) triangular.
It is used in the routines xTRSNA and xTRSEN, but it is also of independent
interest.
for A, given
matrices A, B and C, with A and B (quasi) triangular.
It is used in the routines xTRSNA and xTRSEN, but it is also of independent
interest.
 , where
U and V are orthogonal, and
, where
U and V are orthogonal, and
 , r = min(m , n),
with
, r = min(m , n),
with  . If A is complex, then
its SVD is
. If A is complex, then
its SVD is  where U and V are unitary,
and
where U and V are unitary,
and  if
A is real (
if
A is real ( if A is complex), where
if A is complex), where  and
and  are orthogonal (unitary if A is complex), and B is real and
upper-bidiagonal when m > = n and lower bidiagonal when m < n, so
that B is nonzero only on the main diagonal and either on the first
superdiagonal (if m > = n) or the first subdiagonal (if m < n).
are orthogonal (unitary if A is complex), and B is real and
upper-bidiagonal when m > = n and lower bidiagonal when m < n, so
that B is nonzero only on the main diagonal and either on the first
superdiagonal (if m > = n) or the first subdiagonal (if m < n).
 ,
where
,
where  and
and  are orthogonal and
are orthogonal and  and
and
 .
.
 , then the SVD of A is given by
, then the SVD of A is given by
 .
Similarly, if m << n, it may be more efficient to first perform an
LQ factorization of A, using xGELQF. These preliminary QR and LQ
.
Similarly, if m << n, it may be more efficient to first perform an
LQ factorization of A, using xGELQF. These preliminary QR and LQ
 be the leading k-by-k submatrix of
be the leading k-by-k submatrix of  be the matrix consisting of the first k columns of V.
Then the solution is given by:
be the matrix consisting of the first k columns of V.
Then the solution is given by:
 .
.  can be computed using xORMBR, and
can be computed using xORMBR, and
 .
.
 or
or  (
( or
or  in the Hermitian case).
In the case
in the Hermitian case).
In the case  , if A and B are banded then this may also
be exploited to get a faster algorithm.
, if A and B are banded then this may also
be exploited to get a faster algorithm.

 ,
where C is the symmetric matrix
,
where C is the symmetric matrix  and
and  .
In the complex case C is Hermitian with
.
In the complex case C is Hermitian with  and
and  .
.


 or
or  ,
we use a ``split Cholesky'' factorization
,
we use a ``split Cholesky'' factorization 
 if B is complex), where:
if B is complex), where:
 upper triangular and
upper triangular and  lower triangular of
order approximately n / 2;
S has the same bandwidth as B. After B has been factorized in this way
by the routine
xPBSTF
lower triangular of
order approximately n / 2;
S has the same bandwidth as B. After B has been factorized in this way
by the routine
xPBSTF (where the superscript H denotes conjugate-transpose)
is called
the left generalized eigenvector
(where the superscript H denotes conjugate-transpose)
is called
the left generalized eigenvector , by which we mean
Bx = 0.
Note that if A is non-singular, then the equivalent problem
, by which we mean
Bx = 0.
Note that if A is non-singular, then the equivalent problem
 is perfectly well-behaved, and the infinite eigenvalue
corresponds to
is perfectly well-behaved, and the infinite eigenvalue
corresponds to  .
To deal with infinite eigenvalues,
the LAPACK routines return two values,
.
To deal with infinite eigenvalues,
the LAPACK routines return two values,
 and
and  .
The first basic task of these routines is to compute the
all n pairs
.
The first basic task of these routines is to compute the
all n pairs  and x and/or y for a given
pair of matrices A,B.
and x and/or y for a given
pair of matrices A,B.
 (in the presence of roundoff,
(in the presence of roundoff,  and
and  and
and  , where Q and Z are unitary and
S and P are upper triangular.
The LAPACK routines normalize P
, where Q and Z are unitary and
S and P are upper triangular.
The LAPACK routines normalize P ,
and so the LAPACK routines return
,
and so the LAPACK routines return
 and
and  . The generalized Schur
form depends on the order on which the eigenvalues appear on the
diagonal. In a future version of LAPACK, we will supply routines
to allow the user to choose this order.
. The generalized Schur
form depends on the order on which the eigenvalues appear on the
diagonal. In a future version of LAPACK, we will supply routines
to allow the user to choose this order.
 ,
,  ,
where Q and Z are orthogonal,
P is upper triangular,
and S is quasi-upper triangular
with 1-by-1 and 2-by-2 blocks on the diagonal.
The 1-by-1 blocks correspond to real generalized eigenvalues,
while the 2-by-2 blocks correspond to complex conjugate
pairs of generalized eigenvalues.
In this case, P
,
where Q and Z are orthogonal,
P is upper triangular,
and S is quasi-upper triangular
with 1-by-1 and 2-by-2 blocks on the diagonal.
The 1-by-1 blocks correspond to real generalized eigenvalues,
while the 2-by-2 blocks correspond to complex conjugate
pairs of generalized eigenvalues.
In this case, P and
and  and
and  and
and  .
.
 ,
,  where H is upper Hessenberg (zero below the first subdiagonal), T is
upper triangular and U and V are orthogonal. If A and B are complex,
the decomposition is
where H is upper Hessenberg (zero below the first subdiagonal), T is
upper triangular and U and V are orthogonal. If A and B are complex,
the decomposition is  ,
,  with U and V unitary and
H and T as before.
This decomposition is performed by the subroutine xGGHRD,
with U and V unitary and
H and T as before.
This decomposition is performed by the subroutine xGGHRD,
 ,
,  (for H and T real) or
(for H and T real) or
 ,
,  (for H and T complex) by subroutine xHGEQZ.
(for H and T complex) by subroutine xHGEQZ.
 and
and 
 and
and  are nonsingular upper triangular, and
are nonsingular upper triangular, and
 does not appear,
and
does not appear,
and 



 and
and
 floating-point operations on
floating-point operations on  data, whereas the Level 2 BLAS
perform only
data, whereas the Level 2 BLAS
perform only 
 . Writing these equations as:
. Writing these equations as:













 , where P is a
permutation matrix, and D is block diagonal with blocks of order 1
or 2. A block form of this algorithm has been derived,
and is implemented in the LAPACK routine SSYTRF
, where P is a
permutation matrix, and D is block diagonal with blocks of order 1
or 2. A block form of this algorithm has been derived,
and is implemented in the LAPACK routine SSYTRF







 flops. So eventually the cost of finding eigenvalues
alone becomes small compared to the cost of reduction. However, SSTERF
does only scalar floating point operations, without scope for the BLAS,
so n may have to be large before SSYTRD is slower than SSTERF.
flops. So eventually the cost of finding eigenvalues
alone becomes small compared to the cost of reduction. However, SSTERF
does only scalar floating point operations, without scope for the BLAS,
so n may have to be large before SSYTRD is slower than SSTERF.

 and
and  are tridiagonal, and H is a very simple rank-one matrix.
Then the eigenvalues and eigenvectors of
are tridiagonal, and H is a very simple rank-one matrix.
Then the eigenvalues and eigenvectors of  and
and
 , where
, where  is a diagonal matrix of eigenvalues,
and the columns of
is a diagonal matrix of eigenvalues,
and the columns of  are orthonormal eigenvectors. Thus
are orthonormal eigenvectors. Thus
 is again a simple rank-one matrix. The eigenvalues and eigenvectors
of
is again a simple rank-one matrix. The eigenvalues and eigenvectors
of  may be found
using
may be found
using  Substituting this into the last displayed expression yields
Substituting this into the last displayed expression yields
 are the eigenvectors.
Almost all the work is done in the two matrix multiplies of
are the eigenvectors.
Almost all the work is done in the two matrix multiplies of  , which is done using the Level 3 BLAS.
, which is done using the Level 3 BLAS.

 in the tables.
The performance information for the BLAS routines
in the tables.
The performance information for the BLAS routines  )
) 









 . Machine epsilon bounds the roundoff in individual
floating-point operations.
It may be loosely defined as the largest relative error
. Machine epsilon bounds the roundoff in individual
floating-point operations.
It may be loosely defined as the largest relative error
 in the error bounds.
in the error bounds.

 and
and  are floating-point numbers
are floating-point numbers is any one of the four operations +,
is any one of the four operations +,  ,
,  ,
and
,
and  is the floating-point result of
is the floating-point result of  .
Machine epsilon,
.
Machine epsilon, 


 . In IEEE arithmetic, this
ratio is
. In IEEE arithmetic, this
ratio is  ,
meaning that one expects the double precision answer to have approximately nine
more decimal digits correct than the single precision answer.
,
meaning that one expects the double precision answer to have approximately nine
more decimal digits correct than the single precision answer.
 be an approximation of
the true answer
be an approximation of
the true answer  . We can measure the difference between
. We can measure the difference between  and
and  either by the absolute error
either by the absolute error
 , or, if
, or, if  is nonzero, by the relative error
is nonzero, by the relative error
 . Alternatively, it is sometimes more convenient
to use
. Alternatively, it is sometimes more convenient
to use  instead of the standard expression
for relative error (see section
instead of the standard expression
for relative error (see section  is, say
is, say  , then we say that
, then we say that
 is accurate to 5 decimal digits.
is accurate to 5 decimal digits.
 , which we denote
, which we denote
 . This is read the infinity norm of x.
See Table
. This is read the infinity norm of x.
See Table 
 is an approximation to the
exact vector x, we will refer to
is an approximation to the
exact vector x, we will refer to  as the
absolute error in
as the
absolute error in  as the relative error
in
as the relative error
in  ). As with scalars,
we will sometimes use
). As with scalars,
we will sometimes use  for the relative error.
As above, if the relative error of
for the relative error.
As above, if the relative error of 

 , but this does not have certain
important mathematical properties that make deriving error bounds
convenient (see section
, but this does not have certain
important mathematical properties that make deriving error bounds
convenient (see section  ,
where A is an m-by-n matrix, or
,
where A is an m-by-n matrix, or
 ;
see Table
;
see Table  is the absolute
error
is the absolute
error ,
,  is the relative error
is the relative error

 , where A
is square and invertible, and p is
, where A
is square and invertible, and p is  or one of the other
possibilities in Table
or one of the other
possibilities in Table 
 (
( ), or similarly
), or similarly  (
( ).
).
 . From this definition, we see that
-x, 2x, or any other nonzero multiple
. From this definition, we see that
-x, 2x, or any other nonzero multiple  of x is also an
eigenvector. In other words, eigenvectors are not unique. This
means we cannot measure the difference between two supposed eigenvectors
of x is also an
eigenvector. In other words, eigenvectors are not unique. This
means we cannot measure the difference between two supposed eigenvectors
 , because this may
be large while
, because this may
be large while  is small or even zero for
some
is small or even zero for
some  . This is true
even if we normalize n so that
. This is true
even if we normalize n so that  , since both
x and -x can be normalized simultaneously. So in order to define
error in a useful way, we need to instead consider the set S of
all scalar multiples
, since both
x and -x can be normalized simultaneously. So in order to define
error in a useful way, we need to instead consider the set S of
all scalar multiples  of
x. The set S is
called the subspace spanned by x, and is uniquely determined
by any nonzero member of S. We will measure the difference
between two such sets by the acute angle between them.
Suppose
of
x. The set S is
called the subspace spanned by x, and is uniquely determined
by any nonzero member of S. We will measure the difference
between two such sets by the acute angle between them.
Suppose  is spanned by
is spanned by  and
S is spanned by {x}. Then the acute angle between
and
S is spanned by {x}. Then the acute angle between

 does not change when either
does not change when either

 for any
nonzero scalars
for any
nonzero scalars  .
.
 between
between  ).
Then there is a scalar
).
Then there is a scalar 
 holds when
holds when  is much less than 1
(less than .1 will do nicely). If
is much less than 1
(less than .1 will do nicely). If  ,
where x is a true eigenvector, there is another true eigenvector
,
where x is a true eigenvector, there is another true eigenvector
 .
For example, if
.
For example, if
 for
for  .
.
 in the approximation
in the approximation
 of the true solution
of the true solution  has a drawback: it often cannot
be computed directly, because it depends on the unknown quantity
has a drawback: it often cannot
be computed directly, because it depends on the unknown quantity
 . However, we can often instead estimate
. However, we can often instead estimate
 , since
, since  is
known (it is the output of our algorithm). Fortunately, these two
quantities are necessarily close together, provided either one is small,
which is the only time they provide a useful bound anyway. For example,
is
known (it is the output of our algorithm). Fortunately, these two
quantities are necessarily close together, provided either one is small,
which is the only time they provide a useful bound anyway. For example,
 implies
implies
 , and
, and
 , where p is one of
1, 2,
, where p is one of
1, 2,  such that
such that  , where
n is the dimension of x.
, where
n is the dimension of x.

 such that
such that  , where
A is m-by-n.
, where
A is m-by-n.

 , is also called the spectral
norm of A, and is equal to the largest singular value
, is also called the spectral
norm of A, and is equal to the largest singular value
 of A.
We shall also need to refer to the smallest singular value
of A.
We shall also need to refer to the smallest singular value
 of A; its value can be defined in a similar way to
the definition of the two-norm in Table
of A; its value can be defined in a similar way to
the definition of the two-norm in Table  when A
has at least as many rows as columns, and defined as
when A
has at least as many rows as columns, and defined as
 when A has more
columns than rows. The two-norm,
Frobenius norm
when A has more
columns than rows. The two-norm,
Frobenius norm , they determine
a subspace S consisting of all their possible linear combinations
, they determine
a subspace S consisting of all their possible linear combinations
 ,
,  . We also
say that
. We also
say that  and
and  to
to  between
between

 satisfies
satisfies  . Suppose also that
the vectors
. Suppose also that
the vectors  also
satisfies
also
satisfies  .
Then there is a simple expression for the angle between
.
Then there is a simple expression for the angle between


 .
.
 .
This is because we can not rule out the extremely unlikely possibility of rounding
errors all adding together instead of canceling on average. Using
.
This is because we can not rule out the extremely unlikely possibility of rounding
errors all adding together instead of canceling on average. Using
 :
Gaussian elimination. This typically occurs only on specially constructed
matrices presented in numerical analysis courses [p. 212]wilkinson1.
However, the expert drivers for solving linear systems, xGESVX and xGBSVX,
:
Gaussian elimination. This typically occurs only on specially constructed
matrices presented in numerical analysis courses [p. 212]wilkinson1.
However, the expert drivers for solving linear systems, xGESVX and xGBSVX, where
where  .
. .
Then we have the simple error estimate
.
Then we have the simple error estimate
 is
moderate, the error alg(z) - f(z) will be small
is
moderate, the error alg(z) - f(z) will be small
 by the product of
the condition number of
f at z,
by the product of
the condition number of
f at z,  , and the
relative backward error
, and the
relative backward error  .
.
 and
and  . The conventional (and coarsest) error analysis
uses a norm such as the infinity norm. We therefore call
this normwise backward stability.
. The conventional (and coarsest) error analysis
uses a norm such as the infinity norm. We therefore call
this normwise backward stability.
 satisfying
satisfying  where
where
 and
and
 are both small (close to machine epsilon).
In this case the condition number is
are both small (close to machine epsilon).
In this case the condition number is
 (see section
(see section  operations to solve Ax = b
for a general matrix A, and computing
operations to solve Ax = b
for a general matrix A, and computing  exactly costs
an additional
exactly costs
an additional  operations, or twice as much.
But
operations, or twice as much.
But  ), it confirms that the computed
answer may be completely inaccurate, and so the exact magnitude
of the condition estimate conveys little information.
), it confirms that the computed
answer may be completely inaccurate, and so the exact magnitude
of the condition estimate conveys little information.
 to measure the backward error,
entries of equal magnitude in
to measure the backward error,
entries of equal magnitude in  . This means that
if z is sparse or has some very tiny entries, a normwise backward
stable algorithm may make very large changes in these entries
compared to their original values. If these tiny values are known accurately
by the user, these errors may be unacceptable,
or the error bounds may be unacceptably large.
. This means that
if z is sparse or has some very tiny entries, a normwise backward
stable algorithm may make very large changes in these entries
compared to their original values. If these tiny values are known accurately
by the user, these errors may be unacceptable,
or the error bounds may be unacceptably large.
 .
The usual error bound is approximately
.
The usual error bound is approximately
 ,
which can arbitrarily overestimate the true error,
,
which can arbitrarily overestimate the true error,  is tiny and another one is large.
is tiny and another one is large.
 .
This backward error retains both the sparsity structure of z as
well as the information in tiny entries. These algorithms are therefore
called componentwise relatively backward stable.
Furthermore, computed error bounds reflect this stronger form of backward
error
.
This backward error retains both the sparsity structure of z as
well as the information in tiny entries. These algorithms are therefore
called componentwise relatively backward stable.
Furthermore, computed error bounds reflect this stronger form of backward
error is a small relative change in
is a small relative change in  is a small relative change in
is a small relative change in  . In particular, if A is diagonal,
the corresponding error bound is always tiny, as one would
expect (see the next section).
. In particular, if A is diagonal,
the corresponding error bound is always tiny, as one would
expect (see the next section).

 ,
,

 ,
,
 ,
the true reciprocal condition number
,
the true reciprocal condition number  ,
,
 , and the true error
, and the true error
 .
.

 ,
,
 ,
and the actual error is
,
and the actual error is  .
.
 . In the absence of rounding error r
would be zero and
. In the absence of rounding error r
would be zero and 
 is given by
is given by
 ,
where p(n) is a modestly growing function of n.
The corresponding condition number is
,
where p(n) is a modestly growing function of n.
The corresponding condition number is
 .
.
 is bounded by
is bounded by
 ,
which is
,
which is  in the numerical example,
is approximated by
in the numerical example,
is approximated by  .
Approximations
.
Approximations EPSMCH to
avoid overflow in computing
ERRBD.
EPSMCH to
avoid overflow in computing
ERRBD. and scale the columns by the factors returned in
and scale the columns by the factors returned in
 ,
resulting in
,
resulting in  .
.

 is given by
is given by
 ,
where p(n) is a modestly growing function of n.
In other words,
,
where p(n) is a modestly growing function of n.
In other words,  .
.

 , which is called BERR
, which is called BERR , called FERR
, called FERR
 given above:
given above:
 is the computed value of the residual
is the computed value of the residual  , and
the norm in the numerator is estimated using the same estimation
subroutine used for RCOND.
, and
the norm in the numerator is estimated using the same estimation
subroutine used for RCOND.
 .
.
 .
We discuss error bounds for the most common case where A is m-by-n
with m > n, and A has full rank
.
We discuss error bounds for the most common case where A is m-by-n
with m > n, and A has full rank


 ,
,
 ,
,
 ,
,
 , and the true error
is
, and the true error
is  .
.
 ,
,
 , and the true error is
, and the true error is
 .
.
 , where
E and f satisfy
, where
E and f satisfy

 (approximated by
1/RCOND in the above code fragments),
(approximated by
1/RCOND in the above code fragments),
 (= RNORM above), and
(= RNORM above), and  (SINT = RNORM / BNORM above). Here,
(SINT = RNORM / BNORM above). Here,  is the acute angle between
the vectors
is the acute angle between
the vectors  and
and  is small, the error
is small, the error  is bounded by
is bounded by 
 = COST and
= COST and  = TANT in the code fragments
above.
= TANT in the code fragments
above.
 or
or  instead
of
instead
of  , but these can differ from
, but these can differ from  ) as
exactly zero. The number of singular values treated as nonzero is returned
in RANK. See
) as
exactly zero. The number of singular values treated as nonzero is returned
in RANK. See 
 in the complex Hermitian
case), where Z is orthogonal (unitary) and
in the complex Hermitian
case), where Z is orthogonal (unitary) and
 is real and diagonal,
with
is real and diagonal,
with  .
The
.
The  of
Z are the eigenvectors
of
Z are the eigenvectors . The eigendecomposition of a symmetric matrix is
computed
by the driver routines xSYEV, xSYEVX, xSYEVD, xSBEV, xSBEVX, xSBEVD,
xSPEV, xSPEVX, xSPEVD, xSTEV, xSTEVX and xSTEVD.
The complex counterparts of these routines, which compute the
eigendecomposition of complex Hermitian matrices, are
the driver routines xHEEV, xHEEVX, xHEEVD, xHBEV, xHBEVX, xHBEVD,
xHPEV, xHPEVX, and xHPEVD (see subsection
. The eigendecomposition of a symmetric matrix is
computed
by the driver routines xSYEV, xSYEVX, xSYEVD, xSBEV, xSBEVX, xSBEVD,
xSPEV, xSPEVX, xSPEVD, xSTEV, xSTEVX and xSTEVD.
The complex counterparts of these routines, which compute the
eigendecomposition of complex Hermitian matrices, are
the driver routines xHEEV, xHEEVX, xHEEVD, xHBEV, xHBEVX, xHBEVD,
xHPEV, xHPEVX, and xHPEVD (see subsection 
 , which bound the acute angles
between the computed eigenvectors and true
eigenvectors
, which bound the acute angles
between the computed eigenvectors and true
eigenvectors 


 is nearly
the exact
eigendecomposition of A + E, i.e.,
is nearly
the exact
eigendecomposition of A + E, i.e.,
 is a true eigendecomposition so that
is a true eigendecomposition so that  is
orthogonal,
where
is
orthogonal,
where  and
and
 . Here p(n) is a modestly growing
function of n. We take p(n) = 1 in the above code fragment.
Each computed eigenvalue
. Here p(n) is a modestly growing
function of n. We take p(n) = 1 in the above code fragment.
Each computed eigenvalue  differs from a
true
differs from a
true 
 )
are computed to high relative accuracy
)
are computed to high relative accuracy  and a true unit eigenvector
and a true unit eigenvector 
 is the
absolute gap
is the
absolute gap , where
, where  is a subset of the
integers from 1 to n. Let S be the corresponding true subspace. Then
is a subset of the
integers from 1 to n. Let S be the corresponding true subspace. Then

 ) by using subroutine xSTEBZ (subsection
) by using subroutine xSTEBZ (subsection
 and
and  .
Then the computed eigenvalues
.
Then the computed eigenvalues

 is moderate, each eigenvalue will be computed
to high relative accuracy,
is moderate, each eigenvalue will be computed
to high relative accuracy, 
 is the relative gap between
is the relative gap between  . Let
. Let  .
Let
.
Let  be the corresponding
computed eigenvalues and eigenvectors, computed by expert driver routine
xGEEVX (see subsection
be the corresponding
computed eigenvalues and eigenvectors, computed by expert driver routine
xGEEVX (see subsection 



 denote the average of
the selected eigenvalues:
denote the average of
the selected eigenvalues:
 ,
and similarly for
,
and similarly for  . We also let
. We also let  denote the subspace spanned by
denote the subspace spanned by  ; it is
called a right invariant subspace because if v is any vector in
; it is
called a right invariant subspace because if v is any vector in  is the corresponding computed subspace.
is the corresponding computed subspace.
 .
Some of the bounds are stated in terms of
.
Some of the bounds are stated in terms of  and others in
terms of
and others in
terms of  ; one may use
; one may use  to approximate
either quantity.
The code fragment in the previous subsection approximates
to approximate
either quantity.
The code fragment in the previous subsection approximates
 by
by  , where
, where  is returned by xGEEVX.
is returned by xGEEVX.
 and
and  .
xGEESX (or xTRSEN) returns two quantities for a selected subset
.
xGEESX (or xTRSEN) returns two quantities for a selected subset
 and
and  .
.
 ), and
is referred to as RCONDV by xGEEVX (or xGEESX).
), and
is referred to as RCONDV by xGEEVX (or xGEESX).

 .
.

 . If k of these disks overlap,
so that any two points inside the k disks can be connected
by a continuous curve lying entirely inside the k disks,
and if no larger set of k + 1 disks has this property,
then exactly k of the
. If k of these disks overlap,
so that any two points inside the k disks can be connected
by a continuous curve lying entirely inside the k disks,
and if no larger set of k + 1 disks has this property,
then exactly k of the 
 , where each diagonal block
, where each diagonal block
 has a selected subset of the eigenvalues of A. Such a decomposition
may be useful in computing functions of matrices, for example.
The goal is to choose a V with a nearly minimum condition number
has a selected subset of the eigenvalues of A. Such a decomposition
may be useful in computing functions of matrices, for example.
The goal is to choose a V with a nearly minimum condition number

 -by-
-by- through
through
 of V span the invariant
subspace
of V span the invariant
subspace , and no other choice of V can make
its condition number smaller than
, and no other choice of V can make
its condition number smaller than 
 , where P is a permutation matrix.
If
, where P is a permutation matrix.
If  . Scaling
can make the matrix norm smaller with respect to the eigenvalues, and so
possibly reduce the inaccuracy contributed by roundoff
. Scaling
can make the matrix norm smaller with respect to the eigenvalues, and so
possibly reduce the inaccuracy contributed by roundoff
 . To use the
bounds for eigenvectors, we also need to take into account that bounds
on rotations of eigenvectors are for the eigenvectors
. To use the
bounds for eigenvectors, we also need to take into account that bounds
on rotations of eigenvectors are for the eigenvectors  of
of
 , or
, or  . One coarse but simple way to do this is
as follows: let
. One coarse but simple way to do this is
as follows: let  be the bound on rotations of
be the bound on rotations of  be the desired bound on rotation of x. Let
be the desired bound on rotation of x. Let 


 are exactly those in which we are
interested. In practice, if the eigenvalues on the diagonal of A
are in the wrong order, routine xTREXC
are exactly those in which we are
interested. In practice, if the eigenvalues on the diagonal of A
are in the wrong order, routine xTREXC



 is hard to
compute. Instead we use the more easily computed underestimate
is hard to
compute. Instead we use the more easily computed underestimate

 .
This underestimation makes our error bounds more conservative.
This approximation of s is called RCONDE in xGEEVX and xGEESX.
.
This underestimation makes our error bounds more conservative.
This approximation of s is called RCONDE in xGEEVX and xGEESX.
 of the matrices
of the matrices  is defined as the smallest singular value of the linear
map in (
is defined as the smallest singular value of the linear
map in ( , i.e.,
, i.e.,

 given the ability to compute T and
given the ability to compute T and
 quickly for arbitrary x.
In our case, multiplying an
arbitrary vector by T
means solving the Sylvester equation (
quickly for arbitrary x.
In our case, multiplying an
arbitrary vector by T
means solving the Sylvester equation ( means solving the same equation with
means solving the same equation with  and
and  . Solving either equation
costs at most
. Solving either equation
costs at most  but we use
but we use  . This approximation to sep is called
RCONDV by xGEEVX and xGEESX.
. This approximation to sep is called
RCONDV by xGEEVX and xGEESX.

 is the Kronecker product of X and Y.
This method is
generally impractical, however, because the matrix whose smallest singular
value we need is m(n - m) dimensional, which can be as large as
is the Kronecker product of X and Y.
This method is
generally impractical, however, because the matrix whose smallest singular
value we need is m(n - m) dimensional, which can be as large as
 . Thus we would require as much as
. Thus we would require as much as  extra workspace and
extra workspace and
 operations, much more than the estimation method of the last
paragraph.
operations, much more than the estimation method of the last
paragraph.
 is diagonal,
with
is diagonal,
with  .
The
.
The  are
are
 ,
which bound the acute angles between the computed singular vectors and true
singular vectors
,
which bound the acute angles between the computed singular vectors and true
singular vectors 


 ,
is nearly the exact SVD of A + E where
,
is nearly the exact SVD of A + E where  ,
and p(m , n) is a modestly growing function of m and n. This means
,
and p(m , n) is a modestly growing function of m and n. This means
 is the true SVD, so that
is the true SVD, so that  and
and  are both orthogonal, where
are both orthogonal, where
 , and
, and
 .
Each computed singular value
.
Each computed singular value  differs from true
differs from true 
 ) are computed to
high relative accuracy
) are computed to
high relative accuracy  and a true
and a true 
 is the
absolute gap
is the
absolute gap must be redefined
as
must be redefined
as  .
The gaps may be easily computed from the array of computed singular values
using function
.
The gaps may be easily computed from the array of computed singular values
using function  and a true vector
and a true vector  , where
, where 




 is the relative gap between
is the relative gap between  and
and  if A and B are complex).
This may also be written
if A and B are complex).
This may also be written  .
.
 and
and
 and
and  .
.
 if A
and B are complex).
This may also be written
if A
and B are complex).
This may also be written  .
.









 is large). It is often the case that the eigenvalues
and eigenvectors are much better conditioned than indicated here.
We mention three ways to get tighter bounds.
The first way is effective when the diagonal entries of B differ
widely in magnitude
is large). It is often the case that the eigenvalues
and eigenvectors are much better conditioned than indicated here.
We mention three ways to get tighter bounds.
The first way is effective when the diagonal entries of B differ
widely in magnitude be a diagonal matrix.
Then replace B by DBD and A by DAD in the above bounds.
be a diagonal matrix.
Then replace B by DBD and A by DAD in the above bounds.
 in the above bounds.
in the above bounds.

 and
and  . Then
. Then
 .
In other words, if
.
In other words, if  is the sine of the acute angle
is the sine of the acute angle  between these
subspaces.
between these
subspaces.
 .
Let
.
Let  ) for the exact
eigenvalue
) for the exact
eigenvalue 
 is a condition number for
eigenvalue
is a condition number for
eigenvalue  , using xPOTRF.
, using xPOTRF.
 , using xPOTRF.
, using xPOTRF.
 ,
,  using xTGSJA. The squares of the generalized singular
using xTGSJA. The squares of the generalized singular

 and
and
 and
and  are called the generalized singular values of the pair A , B.
If
are called the generalized singular values of the pair A , B.
If  is infinite.
For details on the structure of
is infinite.
For details on the structure of  and
and  be the values of
be the values of  and
and 
 can differ greatly in magnitude from
the computed generalized singular value
can differ greatly in magnitude from
the computed generalized singular value
 , even if SERRBD is
close to its minimum
, even if SERRBD is
close to its minimum  and
and  , and similarly
, and similarly  and
and  ) are close together in angle.
(This is related to the chordal distance in
section
) are close together in angle.
(This is related to the chordal distance in
section 

 , and the true errors
are
, and the true errors
are  ,
,  .
.
 and
and
 .
This is nearly the exact GSVD of
A + E and B + F in the following sense. E and F are small:
.
This is nearly the exact GSVD of
A + E and B + F in the following sense. E and F are small:
 ,
,  , and
, and  such that
such that
 ,
,


 and
and  and
and  ,
and let
,
and let  and
and  and
and  .
Let
.
Let
 have full rank n, one can show
have full rank n, one can show 
 and approximate the denominator by
and approximate the denominator by
 in order to compute SERRBD;
STRCON returns an approximation RCOND to
in order to compute SERRBD;
STRCON returns an approximation RCOND to
 .
.
 s and
s and 
 and
and  , whereas
, whereas
 have
have
 and
and  , which
are completely different, even though
, which
are completely different, even though  and
and
 . In this case,
. In this case,  ,
so G is nearly rank-deficient.
,
so G is nearly rank-deficient.
 is
stored overwritten on A, and can be passed to STRCON in order to compute
RCOND. If m < = n, then the
first m rows of
is
stored overwritten on A, and can be passed to STRCON in order to compute
RCOND. If m < = n, then the
first m rows of  as coefficient matrices.
as coefficient matrices.
 operations, where
operations, where
 .
.
 denotes a constant depending on the specified matrix dimensions.
denotes a constant depending on the specified matrix dimensions.
 is the computed
approximation to C = AB, then
is the computed
approximation to C = AB, then







 Factorization
Factorization -by-
-by- subdiagonals
and
subdiagonals
and  superdiagonals may be
stored compactly in a two-dimensional array with
superdiagonals may be
stored compactly in a two-dimensional array with  rows and
rows and  ,
although LAPACK routines work correctly for all values of
,
although LAPACK routines work correctly for all values of  ) for
) for
 .
For example, when
.
For example, when  ,
,  and
and  :
:
 superdiagonals.
superdiagonals.
 if upper triangular, or
if upper triangular, or  if
lower triangular.
if
lower triangular.
 subdiagonals or
superdiagonals, only the upper or lower triangle (as specified by
UPLO) need be stored:
subdiagonals or
superdiagonals, only the upper or lower triangle (as specified by
UPLO) need be stored:
 ) for
) for
 ;
;
 ) for
) for
 .
.
 and
and  :
:
 containing the
subdiagonal and superdiagonal elements in elements
containing the
subdiagonal and superdiagonal elements in elements  .
.
 of a vector of length
of a vector of length  factorization
factorization -by-
-by-
 and
and  are respectively
are respectively  has the form
has the form has the form
has the form
 as:
as: