




Next: Standard Eigenvalue and Singular
Up: Driver Routines
Previous: Linear Least Squares (LLS)
Contents
Index
Generalized Linear Least Squares (LSE and GLM) Problems
Driver routines are provided for two types of generalized linear least squares
problems.
The first is
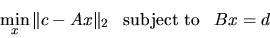 |
(2.2) |
where A is an m-by-n matrix and B is a p-by-n matrix,
c is a given m-vector, and d is a given p-vector,
with
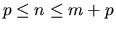 .
This is
called a linear equality-constrained least squares problem (LSE).
The routine xGGLSE
solves this problem using the generalized RQ
(GRQ) factorization, on the
assumptions that B has full row rank p and
the matrix
.
This is
called a linear equality-constrained least squares problem (LSE).
The routine xGGLSE
solves this problem using the generalized RQ
(GRQ) factorization, on the
assumptions that B has full row rank p and
the matrix
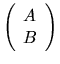 has full column rank n.
Under these assumptions, the problem LSE has a unique solution.
has full column rank n.
Under these assumptions, the problem LSE has a unique solution.
The second generalized linear least squares problem is
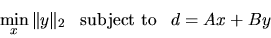 |
(2.3) |
where A is an n-by-m matrix, B is an n-by-p matrix,
and d is a given n-vector,
with
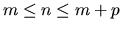 .
This is sometimes called a general (Gauss-Markov) linear model problem (GLM).
When B = I, the problem reduces to an ordinary linear least squares problem.
When B is square and nonsingular, the GLM problem is equivalent to the
weighted linear least squares problem:
.
This is sometimes called a general (Gauss-Markov) linear model problem (GLM).
When B = I, the problem reduces to an ordinary linear least squares problem.
When B is square and nonsingular, the GLM problem is equivalent to the
weighted linear least squares problem:
The routine xGGGLM
solves this problem using the generalized QR (GQR)
factorization, on the
assumptions that A has full column rank m, and the
matrix ( A, B ) has full row rank n. Under these assumptions, the
problem is always consistent, and there are unique solutions x and y.
The driver routines for generalized linear least squares problems are listed
in Table 2.4.
Table 2.4:
Driver routines for generalized linear least squares problems
| Operation |
Single precision |
Double precision |
| |
real |
complex |
real |
complex |
| solve LSE problem using GRQ |
SGGLSE |
CGGLSE |
DGGLSE |
ZGGLSE |
| solve GLM problem using GQR |
SGGGLM |
CGGGLM |
DGGGLM |
ZGGGLM |





Next: Standard Eigenvalue and Singular
Up: Driver Routines
Previous: Linear Least Squares (LLS)
Contents
Index
Susan Blackford
1999-10-01
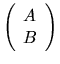 has full column rank n.
Under these assumptions, the problem LSE has a unique solution.
has full column rank n.
Under these assumptions, the problem LSE has a unique solution.