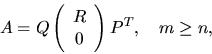
To solve a linear least squares problem (2.1) when A is not of full rank, or the rank of A is in doubt, we can perform either a QR factorization with column pivoting or a singular value decomposition (see subsection 2.4.6).
The QR factorization with column pivoting is given by
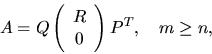
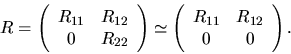
The so-called basic solution to the linear least squares
problem (2.1) can be obtained from this factorization as
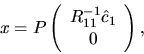
The QR factorization with column pivoting can be computed either by subroutine xGEQPF or by subroutine xGEQP3. Both subroutines compute the factorization but do not attempt to determine the rank of A. xGEQP3 is a Level 3 BLAS version of QR with column pivoting and is considerably faster than xGEQPF, while maintaining the same numerical behavior. The difference between the two routines can best be described as follows. For each column, the subroutine xGEQPF selects one column, permutes it, computes the reflector that zeroes some of its components, and applies it to the rest of the matrix via Level 2 BLAS operations. The subroutine xGEQP3, however, only updates one column and one row of the rest of the matrix (information necessary for the next pivoting phase) and delays the update of the rest of the matrix until a block of columns has been processed. This resulting block of reflectors is then applied to the rest of the matrix as a Level 3 BLAS operation. xGEQPF has been retained for compatibility with Release 2.0 of LAPACK, but we omit references to this routine in the remainder of this users' guide.
For both subroutines, the matrix Q is represented in exactly the same way as after a call of xGEQRF, and so the routines xORGQR and xORMQR can be used to work with Q (xUNGQR and xUNMQR if Q is complex).