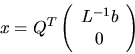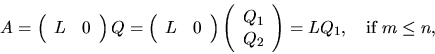
The LQ factorization
is given by
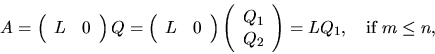
This factorization is computed by the routine xGELQF, and again Q is represented as a product of elementary reflectors; xORGLQ (or xUNGLQ in the complex case) can generate all or part of Q, and xORMLQ (or xUNMLQ ) can pre- or post-multiply a given matrix by Q or QT (QH if Q is complex).
The LQ factorization of A is essentially the same as the QR factorization
of AT (AH if A is complex), since

The LQ factorization may be used to find a minimum norm solution of
an underdetermined system of linear equations A x = b where A is
m-by-n with m < n and has rank m. The solution is given by