The error analysis of the driver routines for the generalized symmetric definite
eigenproblem goes as follows.
In all cases
![]() is
the absolute gap
between
is
the absolute gap
between ![]() and the nearest other eigenvalue.
and the nearest other eigenvalue.
The angular difference between the computed eigenvector
![]() and a true eigenvector zi is
and a true eigenvector zi is
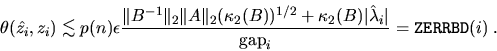
The angular difference between the computed eigenvector
![]() and a true eigenvector zi is
and a true eigenvector zi is
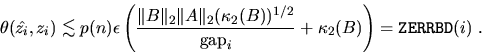
The code fragments above replace p(n) by 1, and makes sure neither RCONDB nor RCONDZ is so small as to cause overflow when used as divisors in the expressions for error bounds.
These error bounds are large when B is ill-conditioned with respect to
inversion (![]() is large). It is often the case that the eigenvalues
and eigenvectors are much better conditioned than indicated here.
We mention three ways to get tighter bounds.
The first way is effective when the diagonal entries of B differ
widely in magnitude4.1:
is large). It is often the case that the eigenvalues
and eigenvectors are much better conditioned than indicated here.
We mention three ways to get tighter bounds.
The first way is effective when the diagonal entries of B differ
widely in magnitude4.1:
The second way to get tighter bounds does not actually supply guaranteed
bounds, but its estimates are often better in practice.
It is not guaranteed because it assumes the algorithm is backward stable,
which is not necessarily true when B is ill-conditioned.
It estimates the chordal distance between a
true eigenvalue ![]() and a computed eigenvalue
and a computed eigenvalue
![]() :
:
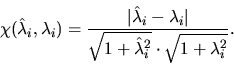
Suppose a computed eigenvalueof
is the exact eigenvalue of a perturbed problem
. Let xi be the unit eigenvector (|xi|2=1) for the exact eigenvalue
. Then if |E| is small compared to |A|, and if |F| is small compared to |B|, we have
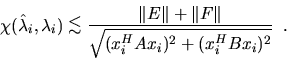
Thusis a condition number for eigenvalue
.
The third way applies only to the first problem ![]() ,
and only
when A is positive definite. We use a different algorithm:
,
and only
when A is positive definite. We use a different algorithm:
Other yet more refined algorithms and error bounds are discussed in [14,95,103].