Error Bounds for the Generalized Nonsymmetric Eigenproblem

We start by stating the simplest error bounds for individual eigenvalues and eigenvectors and leave the more complicated ones to subsequent subsections.

As discussed in section 2.4.8 , from a computational point of view it is more natural to define the generalized nonsymmetric eigenvalue problem in the form $\beta A x = \alpha B x$ with $\lambda = \alpha/\beta$ instead of $Ax = \lambda Bx$. The eigenvalue $\lambda$ is represented as a pair $(\alpha,\beta)$, where a finite eigenvalue has $\beta \neq 0$ and an infinite eigenvalue has $\beta = 0$. As in the standard nonsymmetric eigenvalue problem we have both right and left eigenvectors $x \neq 0$ and $y \neq 0$, respectively, defined as

$$\beta A x = \alpha B x, \quad \beta y^H A = \alpha y^H B .$$ (4.8)

Error bounds for eigenvalues are stated in terms of the distance between pairs $(\alpha,\beta)$ and $(\alpha',\beta')$. Let $\lambda = \alpha/\beta$ and $\lambda' = \alpha'/\beta'$. Then the chordal distance between $\lambda$ and $\lambda'$ (see section 4.10.1) can equivalently be expressed as the chordal distance between two pairs:

$${\cal X}( \lambda,\lambda') = {\cal X}((\alpha, \beta), (\al... ...beta\vert^2} \sqrt{\vert\alpha'\vert^2 + \vert\beta'\vert^2}}.$$ (4.9)

Now we state our error bounds. Let $({\alpha}_i, {\beta}_i), i = 1, \ldots, n$ be the eigenvalues of (A, B), let x_i be a right eigenvector corresponding to $({\alpha}_i, {\beta}_i)$: ${\beta}_i A x_i = {\alpha}_i B x_i$ and let $({\hat{\alpha}}_i, {\hat{\beta}}_i)$ and $\hat{x}_i$ be the corresponding eigenvalues and eigenvectors computed by the expert driver routine xGGEVX (see subsection 2.3.5.2).

The approximate error bounds^4.10for the computed eigenvalues are

$${\cal X}(({\hat{\alpha}}_i, {\hat{\beta}}_i), ({\alpha}_i, {\beta}_i)) \leq {\tt EERRBD}(i) .$$

The approximate error bounds for the computed eigenvectors $\hat{x}_i$, which bound the acute angles between the computed eigenvectors and the true eigenvectors x_i are

$$\theta(\hat{x}_i, x_i) \leq {\tt VERRBD}(i) .$$

The same bounds also hold for the computed left eigenvectors.

These bounds can be computed by the following code fragment:

      EPSMCH = SLAMCH( 'E' )
*     Compute the generalized eigenvalues and eigenvectors of (A,B)
*     ALPHAR/BETA contains the real parts of the eigenvalues
*     ALPHAI/BETA contains the imaginary parts of the eigenvalues
*     VL contains the left eigenvectors
*     VR contains the right eigenvectors
      CALL SGGEVX( 'P', 'V', 'V', 'B', N, A, LDA, B, LDB, ALPHAR,
     $             ALPHAI, BETA, VL, LDVL, VR, LDVR, ILO, IHI, LSCALE,
     $             RSCALE, ABNRM, BBNRM, RCONDE, RCONDV, WORK, LWORK,
     $             IWORK, BWORK, INFO )
      IF( INFO.GT.0 ) THEN
         PRINT *,'INFO =', info, ' from SGGEVX.'
      ELSE IF( N.GT.0 ) THEN
         ABNORM = SLAPY2( ABNRM, BBNRM )
         DO 10 I = 1,N
            EERRBD(I) = EPSMCH*ABNORM/RCONDE(I)
            VERRBD(I) = EPSMCH*ABNORM/RCONDV(I)
   10    CONTINUE
      END IF

For example, suppose^4.1SLAMCH('E') $= 2^{-24} = 5.960 \cdot 10^{-8}$ and

$$A = \left( \begin{array}{cccc} -132~~ & -88~~ & 84 & 104 \\... ...100.8 \\ 160 & 84 & -80~~ & -132~~ \\ \end{array} \right )$$

and

$$B = \left( \begin{array}{cccc} -60~~ & -50~~ & 40 & 50 \\ ... ... -48~~ \\ 70 & 50 & -40~~ & -60~~ \\ \end{array} \right ).$$

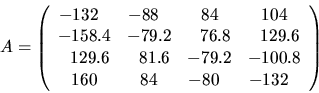
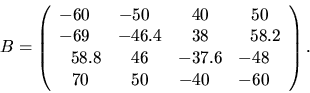
For this problem, the exact eigenvalues, eigenvectors, and eigenvalue condition numbers are known. Then the true eigenvalues, computed eigenvalues, approximate error bounds, and true error bounds are given in the following table.

i	1	2	3	4
$\lambda_i$	1	2	3	4
$\hat{\lambda}_i$	$1.0000529 \cdot 10^0~~$	$1.9999847 \cdot 10^0~~$	$2.9999785 \cdot 10^0~~$	$4.0002117 \cdot 10^0~~$
EERRBD(i)	$9.4562565 \cdot 10^{-5}$	$5.3651773 \cdot 10^{-5}$	$5.6895351 \cdot 10^{-5}$	$1.2976544 \cdot 10^{-4}$
${\cal X}(\hat{\lambda}_i, \lambda_i )$	$3.6398560 \cdot 10^{-5}$	$2.3351108 \cdot 10^{-5}$	$2.2801253 \cdot 10^{-6}$	$1.0059956 \cdot 10^{-5}$
VERRBD(i)	$1.4116328 \cdot 10^{-4}$	$1.4498082 \cdot 10^{-4}$	$6.8483077 \cdot 10^{-4}$	$5.5552053 \cdot 10^{-4}$
$\theta(\hat{l}_i,l_i)$	$1.0050300 \cdot 10^{-5}$	$6.9755580 \cdot 10^{-6}$	$1.3587955 \cdot 10^{-5}$	$4.2988235 \cdot 10^{-6}$
$\theta(\hat{r}_i,r_i)$	$5.2165419 \cdot 10^{-5}$	$1.4475762 \cdot 10^{-5}$	$5.1648690 \cdot 10^{-5}$	$7.9673846 \cdot 10^{-5}$