using the Level 3 BLAS routine xSYR2K; Level 3 BLAS account for at most half the work.
using two calls to the Level 3 BLAS routine xGEMM; Level 3 BLAS account for at most half the work.
Level 3 BLAS account for at most three-quarters of the work.
Eigenvalue problems have also provided a fertile ground for the development of higher performance algorithms. These algorithms generally all consist of three phases: (1) reduction of the original dense matrix to a condensed form by orthogonal transformations, (2) solution of condensed form, and (3) optional backtransformation of the solution of the condensed form to the solution of the original matrix. In addition to block versions of algorithms for phases 1 and 3, a number of entirely new algorithms for phase 2 have recently been discovered. In particular, Version 3.0 of LAPACK includes new block algorithms for the singular value decomposition (SVD) and SVD-based least squares solver, as well as a prototype of a new algorithm xSTEGR[35,87,86,36], which may be the ultimate solution for the symmetric eigenproblem and SVD on both parallel and serial machines.
The first step in solving many types of eigenvalue problems is to reduce the original matrix to a condensed form by orthogonal transformations. In the reduction to condensed forms, the unblocked algorithms all use elementary Householder matrices and have good vector performance. Block forms of these algorithms have been developed [46], but all require additional operations, and a significant proportion of the work must still be performed by Level 2 BLAS, so there is less possibility of compensating for the extra operations.
The algorithms concerned are:
Note that only in the reduction to Hessenberg form is it possible to use the block Householder representation described in subsection 3.4.2. Extra work must be performed to compute the n-by-b matrices X and Y that are required for the block updates (b is the block size) -- and extra workspace is needed to store them.
Nevertheless, the performance gains can be worthwhile on some machines for large enough matrices, for example, on an IBM Power 3, as shown in Table 3.11.
Following the reduction of a dense (or band) symmetric matrix to tridiagonal
form T,
we must compute the eigenvalues and (optionally) eigenvectors of T.
Computing the eigenvalues of T alone (using LAPACK routine
xSTERF) requires
O(n2) flops, whereas the reduction routine
xSYTRD does
![]() flops. So eventually the cost of finding eigenvalues
alone becomes small compared to the cost of reduction. However, xSTERF
does only scalar floating point operations, without scope for the BLAS,
so n may have to be large before xSYTRD is slower than xSTERF.
flops. So eventually the cost of finding eigenvalues
alone becomes small compared to the cost of reduction. However, xSTERF
does only scalar floating point operations, without scope for the BLAS,
so n may have to be large before xSYTRD is slower than xSTERF.
Version 2.0 of LAPACK introduced a new algorithm,
xSTEDC,
for finding all eigenvalues and
eigenvectors of T. The new algorithm can exploit Level 2 and 3 BLAS,
whereas
the previous algorithm,
xSTEQR,
could not. Furthermore, xSTEDC usually does
many
fewer flops than xSTEQR, so the speedup is compounded. Briefly, xSTEDC works
as follows
(for details, see [57,89]). The tridiagonal matrix T is
written as
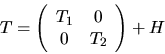
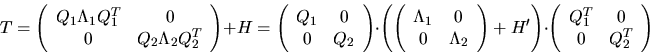
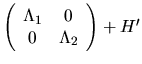 may be found
using O(n2) scalar operations, yielding
may be found
using O(n2) scalar operations, yielding
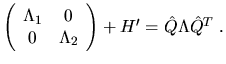 Substituting this into the last displayed expression yields
Substituting this into the last displayed expression yields
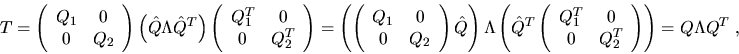
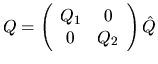 are the eigenvectors.
Almost all the work is done in the two matrix multiplies of Q1 and Q2
times
are the eigenvectors.
Almost all the work is done in the two matrix multiplies of Q1 and Q2
times
The same recursive algorithm has been developed for the singular value decomposition of the bidiagonal matrix resulting from reducing a dense matrix with xGEBRD. The SVD driver using this algorithm is called xGESDD. This recursive algorithm is also used for the SVD-based linear least squares solver xGELSD; see Figure 3.3 to see how much faster DGELSD is than its older routine DGELSS. SBDSQR, Comparison timings of DGESVD and DGESDD can be found in Tables 3.18 and 3.19.
Version 3.0 of LAPACK introduced another new algorithm, xSTEGR, for finding all the eigenvalues and eigenvectors of a symmetric tridiagonal matrix. It is usually even faster than xSTEDC above, and we expect it to ultimately replace all other LAPACK algorithm for the symmetric eigenvalue problem and SVD. Here is a rough description of how it works; for details see [35,87,86,36].
It is easiest to think of xSTEGR as a variation on xSTEIN, inverse iteration. If all the eigenvalues were well separated, xSTEIN would run in O(n2) time. But it is difficult for xSTEIN to compute accurate eigenvectors belonging to close eigenvalues, those that have four or more decimals in common with their neighbors. Indeed, xSTEIN slows down because it reorthogonalizes the corresponding eigenvectors. xSTEGR escapes this difficulty by exploiting the invariance of eigenvectors under translation.
For each cluster ![]() of close eigenvalues the algorithm chooses
a shift s at one end of
of close eigenvalues the algorithm chooses
a shift s at one end of ![]() ,
or just outside, with the property
that T - sI permits triangular factorization
LDLT = T - sI
such that the small shifted eigenvalues
(
,
or just outside, with the property
that T - sI permits triangular factorization
LDLT = T - sI
such that the small shifted eigenvalues
(![]() for
for
![]() )
are determined to high relative accuracy by the
entries in L and D. Note that the small shifted eigenvalues
will have fewer digits in common than those in
)
are determined to high relative accuracy by the
entries in L and D. Note that the small shifted eigenvalues
will have fewer digits in common than those in ![]() .
The algorithm
computes these small shifted eigenvalues to high relative
accuracy, either by xLASQ2
or by refining earlier approximations
using bisection. This means that each computed
.
The algorithm
computes these small shifted eigenvalues to high relative
accuracy, either by xLASQ2
or by refining earlier approximations
using bisection. This means that each computed ![]() approximating a
approximating a ![]() has error bounded by
has error bounded by
![]() .
.
The next task is to compute an eigenvector for ![]() .
For each
.
For each
![]() the algorithm computes, with care, an optimal
twisted factorization
the algorithm computes, with care, an optimal
twisted factorization
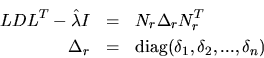
The procedure described above is repeated for any eigenvalues that
remain without eigenvectors. It can be shown that all the computed
z's are very close to eigenvectors of small relative perturbations of
one global Cholesky factorization GGT of a translate ![]() of T. A key
component of the algorithm is the use of recently discovered
differential qd algorithms to ensure that the twisted factorizations
described above are computed without ever forming the indicated
matrix products such as LDLT [51].
of T. A key
component of the algorithm is the use of recently discovered
differential qd algorithms to ensure that the twisted factorizations
described above are computed without ever forming the indicated
matrix products such as LDLT [51].
For computing the eigenvalues and eigenvectors of a Hessenberg matrix--or rather for computing its Schur factorization-- yet another flavor of block algorithm has been developed: a multishift QR iteration [9]. Whereas the traditional EISPACK routine HQR uses a double shift (and the corresponding complex routine COMQR uses a single shift), the multishift algorithm uses block shifts of higher order. It has been found that often the total number of operations decreases as the order of shift is increased until a minimum is reached typically between 4 and 8; for higher orders the number of operations increases quite rapidly. On many machines the speed of applying the shift increases steadily with the order, and the optimum order of shift is typically in the range 8-16. Note however that the performance can be very sensitive to the choice of the order of shift; it also depends on the numerical properties of the matrix. Dubrulle [49] has studied the practical performance of the algorithm, while Watkins and Elsner [101] discuss its theoretical asymptotic convergence rate.
Finally, we note that research into block algorithms for symmetric and nonsymmetric eigenproblems continues [11,68], and future versions of LAPACK will be updated to contain the best algorithms available.