The GSVD algorithm used in LAPACK ([83,10,8]) is backward stable:
Let the computed GSVD of A and B beand
. This is nearly the exact GSVD of A+E and B+F in the following sense. E and F are small:
there exist small,
, and
such that
,
, and
are exactly orthogonal (or unitary):
and
is the exact GSVD of A+E and B+F. Here p(n) is a modestly growing function of n, and we take p(n)=1 in the above code fragment.
Letand
be the square roots of the diagonal entries of the exact
and
, and let
and
the square roots of the diagonal entries of the computed
and
. Let
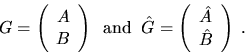
Then provided G andhave full rank n, one can show [96,82] that
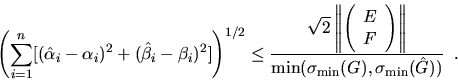
In the code fragment we approximate the numerator of the last expression byand approximate the denominator by
in order to compute SERRBD; STRCON returns an approximation RCOND to
.
We assume that the rank r of G equals n, because otherwise the
![]() s and
s and ![]() s are not well determined. For example, if
s are not well determined. For example, if
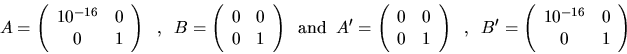
The reason the code fragment assumes ![]() is that in this case
is that in this case ![]() is
stored overwritten on A, and can be passed to STRCON in order to compute
RCOND. If
is
stored overwritten on A, and can be passed to STRCON in order to compute
RCOND. If ![]() ,
then the
first m rows of
,
then the
first m rows of ![]() are
stored in A, and the last n-m rows of
are
stored in A, and the last n-m rows of ![]() are stored in B. This
complicates the computation of RCOND: either
are stored in B. This
complicates the computation of RCOND: either ![]() must be copied to
a single array before calling STRCON, or else the lower level subroutine SLACON
must be used with code capable of solving linear equations with
must be copied to
a single array before calling STRCON, or else the lower level subroutine SLACON
must be used with code capable of solving linear equations with ![]() and
and ![]() as coefficient matrices.
as coefficient matrices.