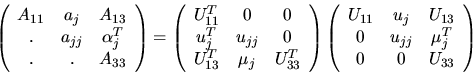
It is comparatively straightforward to recode many of the algorithms in LINPACK and EISPACK so that they call Level 2 BLAS. Indeed, in the simplest cases the same floating-point operations are performed, possibly even in the same order: it is just a matter of reorganizing the software. To illustrate this point we derive the Cholesky factorization algorithm that is used in the LINPACK routine SPOFA, which factorizes a symmetric positive definite matrix as A = UT U. Writing these equations as:
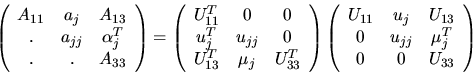
and equating coefficients of the jth column, we obtain:
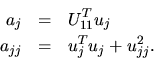
Hence, if U11 has already been computed, we can compute uj and
ujj
from the equations:
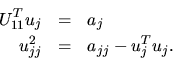
Here is the body of the code of the LINPACK routine SPOFA, which implements the above method:
DO 30 J = 1, N
INFO = J
S = 0.0E0
JM1 = J - 1
IF (JM1 .LT. 1) GO TO 20
DO 10 K = 1, JM1
T = A(K,J) - SDOT(K-1,A(1,K),1,A(1,J),1)
T = T/A(K,K)
A(K,J) = T
S = S + T*T
10 CONTINUE
20 CONTINUE
S = A(J,J) - S
C ......EXIT
IF (S .LE. 0.0E0) GO TO 40
A(J,J) = SQRT(S)
30 CONTINUE
And here is the same computation recoded in ``LAPACK-style'' to use the Level 2 BLAS routine STRSV (which solves a triangular system of equations). The call to STRSV has replaced the loop over K which made several calls to the Level 1 BLAS routine SDOT. (For reasons given below, this is not the actual code used in LAPACK -- hence the term ``LAPACK-style''.)
DO 10 J = 1, N
CALL STRSV( 'Upper', 'Transpose', 'Non-unit', J-1, A, LDA,
$ A(1,J), 1 )
S = A(J,J) - SDOT( J-1, A(1,J), 1, A(1,J), 1 )
IF( S.LE.ZERO ) GO TO 20
A(J,J) = SQRT( S )
10 CONTINUE
This change by itself is sufficient to make big gains in performance on machines like the CRAY C-90.
But on many machines such as an IBM RISC Sys/6000-550 (using double precision) there is virtually no difference in performance between the LINPACK-style and the LAPACK Level 2 BLAS style code. Both styles run at a megaflop rate far below its peak performance for matrix-matrix multiplication. To exploit the faster speed of Level 3 BLAS, the algorithms must undergo a deeper level of restructuring, and be re-cast as a block algorithm -- that is, an algorithm that operates on blocks or submatrices of the original matrix.
To derive a block form of Cholesky
factorization, we write the
defining equation in partitioned form thus:
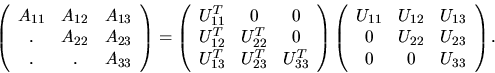
Equating submatrices in the second block of columns, we obtain:
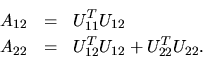
Hence, if U11 has already been computed, we can compute U12 as
the solution to the equation
U11T U12 = A12
DO 10 J = 1, N, NB
JB = MIN( NB, N-J+1 )
CALL STRSM( 'Left', 'Upper', 'Transpose', 'Non-unit', J-1, JB,
$ ONE, A, LDA, A( 1, J ), LDA )
CALL SSYRK( 'Upper', 'Transpose', JB, J-1, -ONE, A( 1, J ), LDA,
$ ONE, A( J, J ), LDA )
CALL SPOTF2( 'Upper', JB, A( J, J ), LDA, INFO )
IF( INFO.NE.0 ) GO TO 20
10 CONTINUE
But that is not the end of the story, and the code given above is not the code that is actually used in the LAPACK routine SPOTRF. We mentioned in subsection 3.1.1 that for many linear algebra computations there are several vectorizable variants, often referred to as i-, j- and k-variants, according to a convention introduced in [45] and used in [55]. The same is true of the corresponding block algorithms.
It turns out that the j-variant that was chosen for LINPACK, and used in the above examples, is not the fastest on many machines, because it is based on solving triangular systems of equations, which can be significantly slower than matrix-matrix multiplication. The variant actually used in LAPACK is the i-variant, which does rely on matrix-matrix multiplication.