




Next: Algorithm
Up: Hermitian Eigenvalue Problems
Previous: Software Availability
Contents
Index
Lanczos Method
A. Ruhe
The Lanczos algorithm is closely related to the iterative
algorithms discussed in the previous section in that it
needs to access the matrix only in the form of matrix-vector
operations. It is different in that it makes much
better use of the information obtained by remembering all
the directions computed and always lets the matrix operate on a vector
orthogonal to all those previously tried.
In this section we describe the Hermitian Lanczos algorithm
applicable to the eigenvalue
problem,
 |
(20) |
where  is a Hermitian, or in the real case symmetric, matrix
operator.
is a Hermitian, or in the real case symmetric, matrix
operator.
The algorithm starts with a properly chosen starting vector 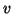 and builds up an
orthogonal basis
and builds up an
orthogonal basis 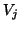 of the Krylov subspace,
of the Krylov subspace,
 |
(21) |
one column at a time. In each step just one matrix-vector
multiplication
 |
(22) |
is needed. In the new orthogonal basis 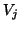 the operator
the operator  is
represented by a real symmetric tridiagonal matrix,
is
represented by a real symmetric tridiagonal matrix,
![\begin{displaymath}
T_{j}=\left[
\begin{array}{cccc}\alpha_1 & \beta_1 &&\\
\be...
...beta_{j-1}\\
&&\beta_{j-1}&\alpha_j\\
\end{array} \right]\;,
\end{displaymath}](img859.png) |
(23) |
which is also built up one row and column at a time, using the basic
recursion,
 |
(24) |
At any step  , we may
compute an eigensolution of
, we may
compute an eigensolution of 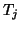 ,
,
 |
(25) |
where the superscript 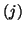 is used to indicate that these quantities change
for each iteration
is used to indicate that these quantities change
for each iteration  . The Ritz value
. The Ritz value
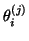 and its Ritz
vector,
and its Ritz
vector,
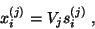 |
(26) |
will be a good approximation to an eigenpair of  if the residual
has small norm; see §4.8.
if the residual
has small norm; see §4.8.
Let us compute the residual for this Ritz pair,
We see that its norm satisfies
 |
(27) |
so we need to monitor only the subdiagonal elements 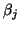 of
of 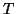 and the last elements
and the last elements 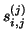 of its eigenvectors to get an
estimate of the norm of the residual. As soon as this estimate is
small, we may flag the Ritz value
of its eigenvectors to get an
estimate of the norm of the residual. As soon as this estimate is
small, we may flag the Ritz value
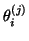 as
converged to the eigenvalue
as
converged to the eigenvalue 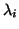 . Note that
the computation of the Ritz values does not need
the matrix-vector
multiplication (4.12). We can save this time-consuming
operation until the step
. Note that
the computation of the Ritz values does not need
the matrix-vector
multiplication (4.12). We can save this time-consuming
operation until the step  , when the estimate (
, when the estimate (![[*]](http://www.netlib.org/utk/icons/crossref.png) ) indicates convergence.
) indicates convergence.
Subsections





Next: Algorithm
Up: Hermitian Eigenvalue Problems
Previous: Software Availability
Contents
Index
Susan Blackford
2000-11-20
![]() and builds up an
orthogonal basis
and builds up an
orthogonal basis ![]() of the Krylov subspace,
of the Krylov subspace,