




Next: 11.1.1 Load Balancing a
Up: 11 Load Balancing and
Previous: 11 Load Balancing and
We have seen many times that parallel computing involves breaking
problems into parts which execute concurrently. In the simple regular
problems seen in the early chapters, especially Chapters 4
and 6, it was usually reasonably obvious how to
perform this breakup to optimize performance of the program on a
parallel machine. However, in Chapter 9 and even more so in
Chapter 12, we will find that the nature of the parallelism is
as clear as before, but that it is nontrivial to implement
efficiently.
Irregular loosely synchronous problems consist of a collection of
heterogeneous tasks communicating with each other at the
macrosynchronization points characteristic of this problem class. Both
the execution time per task and amount and pattern of communication can
differ from task to task. In this section, we describe and compare
several approaches to this problem. We note that formally this is a
very hard-so-called NP-complete-optimization problem. With
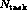 tasks running on
tasks running on 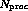 processors we
cannot afford to examine every one of the
processors we
cannot afford to examine every one of the 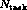
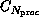 assignments of tasks to processors.
Experience has shown that this problem is easier than one would have
thought-partly at least because one does not require the exactly
optimal assignment. Rather, a solution whose execution time is, say,
within 10% of the optimal value is quite acceptable. Remember, one
has probably chosen to ``throw away'' a larger fraction than this of
the possible MPP performance by using a high-level language such as
Fortran or C on the node (independent of any parallelism issues). The
physical optimization
methods described in Section 11.3 and more problem-specific
heuristics have shown themselves very suitable for
this class of approximate optimization [Fox:91j;92i].
In 1985, at a DOE contract renewal review at Caltech,
we thought that this load balancing issue would be a major and perhaps
the key stumbling block for parallel computing. However, this is not
the case-it is a hard and important problem, but for loosely
synchronous problems it can be solved straightforwardly
[Barnard:93a], [Fox:92c;92h;92i],
[Fox:92h] [Mansour:92d]. Our approach to
this uses physical analogies and stems in fact from dinner
conversations between Fox and David Jefferson, a collaborator from
UCLA, at this meeting
[Fox:85k;86a;88e;88mm]. An
interesting computer science challenge is to understand why the
NP-complete load-balancing problem appears ``easier
in practice'' than the Travelling Salesman Problem, which is the
generic NP-complete optimization problem. We will return to this
briefly in Section 11.3, but note that the ``shape of the
objection function'' (in physics language, the ``energy landscape'')
illustrated in Figure 11.1 appears critical. Load-balancing
problems appear to fall into the ``easy class'' of NP-complete
optimization problems with the landscape of Figure 11.1(a).
The methods discussed in the following are only a sample of the many
effective approaches developed recently: [Barhen:88a],
[Berger:87a], [Chen:88a], [Chrisochoides:91a],
[Ercal:88a], [Ercal:88b],
[Farhat:88a;89b], [Fox:88nn],
[Hammond:92b], [Houstis:90a], [Livingston:88a],
[Miller:92a], [Nolting:91a], [Teng:91a],
[Walker:90b]. The work of Simon [Barnard:93a],
[Pothen:90a], [Simon:91b], [Venkatakrishnan:92a] on
recursive spectral bisection-a method with similarities to the eigenvector recursive bisection (ERB) method mentioned later-has
been particularly successful.
assignments of tasks to processors.
Experience has shown that this problem is easier than one would have
thought-partly at least because one does not require the exactly
optimal assignment. Rather, a solution whose execution time is, say,
within 10% of the optimal value is quite acceptable. Remember, one
has probably chosen to ``throw away'' a larger fraction than this of
the possible MPP performance by using a high-level language such as
Fortran or C on the node (independent of any parallelism issues). The
physical optimization
methods described in Section 11.3 and more problem-specific
heuristics have shown themselves very suitable for
this class of approximate optimization [Fox:91j;92i].
In 1985, at a DOE contract renewal review at Caltech,
we thought that this load balancing issue would be a major and perhaps
the key stumbling block for parallel computing. However, this is not
the case-it is a hard and important problem, but for loosely
synchronous problems it can be solved straightforwardly
[Barnard:93a], [Fox:92c;92h;92i],
[Fox:92h] [Mansour:92d]. Our approach to
this uses physical analogies and stems in fact from dinner
conversations between Fox and David Jefferson, a collaborator from
UCLA, at this meeting
[Fox:85k;86a;88e;88mm]. An
interesting computer science challenge is to understand why the
NP-complete load-balancing problem appears ``easier
in practice'' than the Travelling Salesman Problem, which is the
generic NP-complete optimization problem. We will return to this
briefly in Section 11.3, but note that the ``shape of the
objection function'' (in physics language, the ``energy landscape'')
illustrated in Figure 11.1 appears critical. Load-balancing
problems appear to fall into the ``easy class'' of NP-complete
optimization problems with the landscape of Figure 11.1(a).
The methods discussed in the following are only a sample of the many
effective approaches developed recently: [Barhen:88a],
[Berger:87a], [Chen:88a], [Chrisochoides:91a],
[Ercal:88a], [Ercal:88b],
[Farhat:88a;89b], [Fox:88nn],
[Hammond:92b], [Houstis:90a], [Livingston:88a],
[Miller:92a], [Nolting:91a], [Teng:91a],
[Walker:90b]. The work of Simon [Barnard:93a],
[Pothen:90a], [Simon:91b], [Venkatakrishnan:92a] on
recursive spectral bisection-a method with similarities to the eigenvector recursive bisection (ERB) method mentioned later-has
been particularly successful.
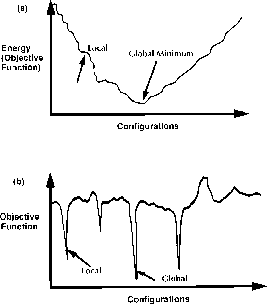
Figure 11.1: Two Possible ``Energy Landscapes'' for an Optimization
Problem
A few general remarks are necessary; we use the phrases ``load
balancing'' and ``data decomposition'' interchangeably. One needs
both ab initio and dynamic distribution and redistribution of data on
the parallel machine. We also can examine load balancing at the level
of data or of tasks that encapsulate the data and
algorithm. In elegant (but currently inefficient) software models
with one datum per task, these formulations are equivalent. Our
examples will do load balancing at the level of data values, but the
task and data distribution problems are essentially equivalent.
Our methods are applicable to general loosely synchronous problems and
indeed can be applied to arbitrary problem classes. However, we will
choose a particular finite-element problem to illustrate the issues
where one needs to distribute a mesh, such as that illustrated in
Figure 11.2. Each triangle or element represents a task
which communicates with its neighboring three triangles. In doing, for
example, a simulation of fluid flow on the mesh, each element of the
mesh communicates regularly with its neighbors, and this pattern may be
repeated thousands of times.

Figure 11.2: An Unstructured Triangular Mesh Surrounding a Four-Element
Airfoil. The mesh is distributed among 16 processors, with divisions
shown by heavy lines.
We may classify load-balancing strategies into four broad types, depending on
when the optimization is made and whether the cost of the optimization is
included in the optimization itself:\
- By Inspection: The load-balancing strategy may be determined
by inspection, such as with a rectangular lattice of grid points split into
smaller rectangles, so that the load-balancing problem is solved before the
program is written. This is illustrated by the QCD decomposition of
Figure 4.3.
- Static: The optimization is nontrivial, but may be done by
a sequential machine before starting the parallel program, so that the
load-balancing problem is solved before the parallel program begins.
- Quasi-Dynamic: The circumstances determining the optimal balance
change during program execution, but discretely and infrequently. Because
the change is discrete, the load-balance problem,
and hence its solution, remain the same until the next change. If
these changes are infrequent enough, any savings made in the subsequent
computation make up for the time spent solving the load-balancing
problem. The difference between this and the static case is that the
load balancing must be carried out in parallel to prevent a sequential
bottleneck.
Koller calls these problems adiabatic [Fox:90nn], using a physical
analogy where the load balancer can be viewed as a heatbath keeping
the problem in equilibrium. In adiabatic systems, changes are
sufficiently slow that the heatbath can ``keep up'' and the system
evolves from equilibrium state to equilibrium state.
- Dynamic: The circumstances determining the optimal
balance change frequently or continuously during execution, so that the
cost of the load balancing calculation after each change should be
minimized in addition to optimizing the splitting of the actual
calculation. This means that there must be a decision made every so
often to decide if load balancing is necessary, and how much time to
spend on it. The chess program in Section 14.3 shows very
irregular dynamic behavior so that statistical load-balancing methods
similar to the scattered decomposition of Section 11.2
must be used.
If the mesh is solution-adaptive, that is, if the mesh, and hence the
load-balancing problem, change discretely during execution of the code,
then it is most efficient to decide the optimal mesh distribution in
parallel. In this section, three parallel algorithms, orthogonal
recursive bisection (ORB), eigenvector
recursive bisection (ERB) and a
simple parallelization of simulated annealing (SA) are discussed for load-balancing a dynamic
unstructured triangular mesh on 16 processors of an nCUBE
machine.
The test problem is a solution-adaptive Laplace
solver, with an initial mesh of 280 elements, refined in seven stages
to 5772 elements. We present execution times for the solver resulting
from the mesh distributions using the three algorithms, as well as
results on imbalance, communication traffic, and element migration.
In this section, we shall consider the quasi-dynamic case with observations
on the time taken to do the load balancing that bear on the dynamic case.
The testbed is an unstructured-mesh finite-element code, where the elements
are the atoms of the problem, which are to be assigned to processors. The
mesh is solution-adaptive, meaning that it becomes finer in places where the
solution of the problem dictates refinement.
We shall show that a class of finite-element applications share common
load-balancing requirements, and formulate load balancing as a graph-coloring
problem. We shall discuss three methods for solving this graph-coloring
problem: one based on statistical physics, one derived from a computational
neural net, and one cheap and simple method.
We present results from running these three load-balancing methods, both in
terms of the quality of the graph-coloring solution (machine-independent
results), and in terms of the particular machine (16 processors of an nCUBE)
on which the test was run.





Next: 11.1.1 Load Balancing a
Up: 11 Load Balancing and
Previous: 11 Load Balancing and
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
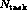 tasks running on
tasks running on 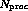 processors we
cannot afford to examine every one of the
processors we
cannot afford to examine every one of the 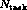
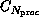 assignments of tasks to processors.
Experience has shown that this problem is easier than one would have
thought-partly at least because one does not require the exactly
optimal assignment. Rather, a solution whose execution time is, say,
within 10% of the optimal value is quite acceptable. Remember, one
has probably chosen to ``throw away'' a larger fraction than this of
the possible MPP performance by using a high-level language such as
Fortran or C on the node (independent of any parallelism issues). The
physical optimization
methods described in Section 11.3 and more problem-specific
heuristics have shown themselves very suitable for
this class of approximate optimization [Fox:91j;92i].
In 1985, at a DOE contract renewal review at Caltech,
we thought that this load balancing issue would be a major and perhaps
the key stumbling block for parallel computing. However, this is not
the case-it is a hard and important problem, but for loosely
synchronous problems it can be solved straightforwardly
[Barnard:93a], [Fox:92c;92h;92i],
[Fox:92h] [Mansour:92d]. Our approach to
this uses physical analogies and stems in fact from dinner
conversations between Fox and David Jefferson, a collaborator from
UCLA, at this meeting
[Fox:85k;86a;88e;88mm]. An
interesting computer science challenge is to understand why the
NP-complete load-balancing problem appears ``easier
in practice'' than the Travelling Salesman Problem, which is the
generic NP-complete optimization problem. We will return to this
briefly in Section 11.3, but note that the ``shape of the
objection function'' (in physics language, the ``energy landscape'')
illustrated in Figure 11.1 appears critical. Load-balancing
problems appear to fall into the ``easy class'' of NP-complete
optimization problems with the landscape of Figure 11.1(a).
The methods discussed in the following are only a sample of the many
effective approaches developed recently: [Barhen:88a],
[Berger:87a], [Chen:88a], [Chrisochoides:91a],
[Ercal:88a], [Ercal:88b],
[Farhat:88a;89b], [Fox:88nn],
[Hammond:92b], [Houstis:90a], [Livingston:88a],
[Miller:92a], [Nolting:91a], [Teng:91a],
[Walker:90b]. The work of Simon [Barnard:93a],
[Pothen:90a], [Simon:91b], [Venkatakrishnan:92a] on
recursive spectral bisection-a method with similarities to the eigenvector recursive bisection (ERB) method mentioned later-has
been particularly successful.
assignments of tasks to processors.
Experience has shown that this problem is easier than one would have
thought-partly at least because one does not require the exactly
optimal assignment. Rather, a solution whose execution time is, say,
within 10% of the optimal value is quite acceptable. Remember, one
has probably chosen to ``throw away'' a larger fraction than this of
the possible MPP performance by using a high-level language such as
Fortran or C on the node (independent of any parallelism issues). The
physical optimization
methods described in Section 11.3 and more problem-specific
heuristics have shown themselves very suitable for
this class of approximate optimization [Fox:91j;92i].
In 1985, at a DOE contract renewal review at Caltech,
we thought that this load balancing issue would be a major and perhaps
the key stumbling block for parallel computing. However, this is not
the case-it is a hard and important problem, but for loosely
synchronous problems it can be solved straightforwardly
[Barnard:93a], [Fox:92c;92h;92i],
[Fox:92h] [Mansour:92d]. Our approach to
this uses physical analogies and stems in fact from dinner
conversations between Fox and David Jefferson, a collaborator from
UCLA, at this meeting
[Fox:85k;86a;88e;88mm]. An
interesting computer science challenge is to understand why the
NP-complete load-balancing problem appears ``easier
in practice'' than the Travelling Salesman Problem, which is the
generic NP-complete optimization problem. We will return to this
briefly in Section 11.3, but note that the ``shape of the
objection function'' (in physics language, the ``energy landscape'')
illustrated in Figure 11.1 appears critical. Load-balancing
problems appear to fall into the ``easy class'' of NP-complete
optimization problems with the landscape of Figure 11.1(a).
The methods discussed in the following are only a sample of the many
effective approaches developed recently: [Barhen:88a],
[Berger:87a], [Chen:88a], [Chrisochoides:91a],
[Ercal:88a], [Ercal:88b],
[Farhat:88a;89b], [Fox:88nn],
[Hammond:92b], [Houstis:90a], [Livingston:88a],
[Miller:92a], [Nolting:91a], [Teng:91a],
[Walker:90b]. The work of Simon [Barnard:93a],
[Pothen:90a], [Simon:91b], [Venkatakrishnan:92a] on
recursive spectral bisection-a method with similarities to the eigenvector recursive bisection (ERB) method mentioned later-has
been particularly successful.






