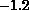 to
to 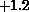 , the lightly shaded
S-shaped internal boundary has voltage +1, and the dark shaded hook-shaped
internal boundary has voltage -1. Contour lines of the solution are also
shown in the figure, with contour interval
, the lightly shaded
S-shaped internal boundary has voltage +1, and the dark shaded hook-shaped
internal boundary has voltage -1. Contour lines of the solution are also
shown in the figure, with contour interval 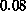 .
.





The applications described in Section 11.1.1 have been implemented with DIME (Distributed Irregular Mesh Environment), described in Section 10.1.
We have tested these three load-balancing methods using the application
code ``Laplace'' described in Section 11.1.1. The problem is
to solve Laplace's equation with Dirichlet boundary conditions, in the domain
shown in Figure 11.13. The square outer boundary has voltage
linearly increasing vertically from 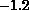 to
to 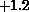 , the lightly shaded
S-shaped internal boundary has voltage +1, and the dark shaded hook-shaped
internal boundary has voltage -1. Contour lines of the solution are also
shown in the figure, with contour interval
, the lightly shaded
S-shaped internal boundary has voltage +1, and the dark shaded hook-shaped
internal boundary has voltage -1. Contour lines of the solution are also
shown in the figure, with contour interval 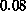 .
.
The test begins with a relatively coarse mesh of 280 elements, all residing in a single processor, with the others having none. The Laplace equation is solved by Jacobi iteration, the mesh is refined based on the solution obtained so far, then is balanced by the method under test. This sequence-solve, refine, balance-is repeated seven times until the final mesh has 5772 elements. The starting and ending meshes are shown in Figure 11.14.

Figure 11.14: Initial and Final Meshes for the Load-Balancing Test. The
initial mesh with 280 elements is essentially a uniform meshing of the
square, and the final mesh of 5772 elements is dominated by the highly
refined S-shaped region in the center.
The refinement is solution-adaptive, so that the set of elements to be refined is based on the solution that has been computed so far. The refinement criterion is the magnitude of the gradient of the solution, so that the most heavily refined part of the domain is that between the S-shaped and hook-shaped boundaries where the contour lines are closest together. At each refinement, the criterion is calculated for each element of the mesh, and a value is found such that a given proportion of the elements are to be refined, and those with higher values than this are refined loosely synchronously. For this test of load balancing, we refined 40% of the elements of the mesh at each stage.
This choice of refinement criterion is not particularly to improve the accuracy of the solution, but to test the load-balancing methods as the mesh distribution changes. The initial mesh is essentially a square covered in mesh of roughly uniform density, and the final mesh is dominated by the long, thin S-shaped region between the internal boundaries, so the mesh changes character from two-dimensional to almost one-dimensional.
We ran this test sequence on 16 nodes of an nCUBE/10 parallel machine, using ORB and ERB and two runs with SA, the difference being a factor of ten in cooling rate, and different starting temperatures.
The eigenvalue recursive bisection used the deflated Lanczos method for diagonalization, with three iterations of 30 Lanczos vectors each to find the second eigenvector. These numbers were chosen so that more iterations and Lanczos vectors produced no significant improvement, and fewer degraded the performance of the algorithm.
The parameters used for the collisional annealing were as follows:\
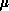 , was set at 0.1, which is
large enough to make communication important in the cost function, but
small enough that all processors will get their share of elements.
, was set at 0.1, which is
large enough to make communication important in the cost function, but
small enough that all processors will get their share of elements.
In Figure 11.15, we show the divisions between processor domains for the three methods at the fifth stage of the refinement, with 2393 elements in the mesh. The figure also shows the divisions for the ORB method at the fourth stage: Note the unfortunate processor division to the left of the S-shaped boundary which is absent at the fifth stage.
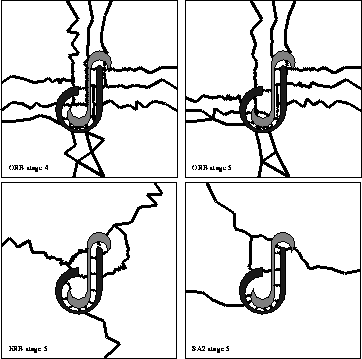
Figure 11.15: Processor Divisions Resulting from the Load-Balancing
Algorithms. Top, ORB at the fourth and fifth stages; lower left, ERB at
the fifth stage; lower right, SA2 at the fifth stage.




