




Next: 11.1.6 Eigenvalue Recursive Bisection
Up: 11.1 Load Balancing as
Previous: 11.1.4 Simulated Annealing
Rather than coloring the graph by direct minimization of the load-balance
cost function, we may do better to reduce the problem to a number of
smaller problems. The idea of recursive bisection is that it is easier to color a graph with two colors than
many colors. We first split the graph into two halves, minimizing the
communication between the halves. We can then color each half with two
colors, and so on, recursively bisecting each subgraph.
There are two advantages to recursive bisection; first, each subproblem
(coloring a graph with two colors) is easier than the general problem;
second, there is natural parallelism. While the first stage is
splitting a single graph in two, and is thus a sequential problem, there is
two-way parallelism at the second stage, when the two halves are being split,
and four-way parallelism when the four quarters are being split. Thus,
coloring a graph with P colors is achieved in a number of stages which is
logarithmic in P.
Both of the recursive bisection methods we shall discuss split a graph into
two by associating a scalar quantity, 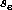 , with each graph node, e, which
we may call a separator field. By evaluating the median S of the
, with each graph node, e, which
we may call a separator field. By evaluating the median S of the
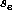 , we can color the graph according to whether
, we can color the graph according to whether 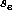 is greater or less
than S. The median is chosen as the division so that the number of nodes
in each half is automatically equal; the problem is now reduced to that of
choosing the field,
is greater or less
than S. The median is chosen as the division so that the number of nodes
in each half is automatically equal; the problem is now reduced to that of
choosing the field, 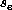 , so that the communication is minimized.
, so that the communication is minimized.
Orthogonal Recursive Bisection
A simple and cheap choice [Fox:88mm] for the separator field is based on
the position of the finite elements in the mesh. We might let the value
of 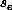 be the x-coordinate of the center of mass of the element, so that
the mesh is split in two by a median line parallel to the y-axis. At the
next stage, we split the submesh by a median line parallel to the x-axis,
alternating between x and y stage by stage, as shown in
Figure 11.11. Another example is shown in
Figure 12.13.
be the x-coordinate of the center of mass of the element, so that
the mesh is split in two by a median line parallel to the y-axis. At the
next stage, we split the submesh by a median line parallel to the x-axis,
alternating between x and y stage by stage, as shown in
Figure 11.11. Another example is shown in
Figure 12.13.

Figure 11.11: Load Balancing by ORB for Four Processors. The elements (left)
are reduced to points at their centers of mass (middle), then split into
two vertically, then each half split into two horizontally. The result
(right) shows the assignment of elements to processors.





Next: 11.1.6 Eigenvalue Recursive Bisection
Up: 11.1 Load Balancing as
Previous: 11.1.4 Simulated Annealing
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
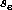 , with each graph node, e, which
we may call a separator field. By evaluating the median S of the
, with each graph node, e, which
we may call a separator field. By evaluating the median S of the
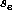 , we can color the graph according to whether
, we can color the graph according to whether 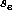 is greater or less
than S. The median is chosen as the division so that the number of nodes
in each half is automatically equal; the problem is now reduced to that of
choosing the field,
is greater or less
than S. The median is chosen as the division so that the number of nodes
in each half is automatically equal; the problem is now reduced to that of
choosing the field, 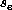 , so that the communication is minimized.
, so that the communication is minimized.





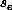 be the x-coordinate of the center of mass of the element, so that
the mesh is split in two by a median line parallel to the y-axis. At the
next stage, we split the submesh by a median line parallel to the x-axis,
alternating between x and y stage by stage, as shown in
Figure
be the x-coordinate of the center of mass of the element, so that
the mesh is split in two by a median line parallel to the y-axis. At the
next stage, we split the submesh by a median line parallel to the x-axis,
alternating between x and y stage by stage, as shown in
Figure 