18.1.2 Asynchronous versus Loosely Synchronous?

  
Table 18.1: Summary of Problem Classes

This is the last chapter on our voyage through the space of problem classes. Thus, we will use this opportunity to wrap up some general issues. We will, in particular, summarize the hardware and software architectures that are suitable for the different problem classes that are reviewed in Table 18.1. We will first sharpen the distinction between loosely synchronous and asynchronous problems. Let us compare,

1. Topology is an irregular two- or three-dimensional graph.

   Loosely Synchronous: Solution of partial differential equation with an unstructured mesh, as in Figure 12.8 (Color Plate).

   Asynchronous: Communication linkage between satellites in three dimensions, as in Figure 3.11(b).

2. Topology is an irregular tree (hierarchical structure).

   Loosely Synchronous: Fast multipole  approach to N-body  problem, as in Figure 12.11.

   Asynchronous: - 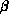pruned game tree coming from computer chess,  as in Figure 14.4.

These examples show that asynchronous and loosely synchronous problems are represented by similar underlying irregular graphs. What are the differences? Notice that we can always treat a loosely synchronous problem as asynchronous and indeed many approaches do this. One just needs to ignore the macroscopic algorithmic synchronization present in loosely synchronous problems. When is this a good idea? One would treat loosely synchronous problems as asynchronous when:

• The resultant (parallel) asynchronous implementation had sufficient performance. The loosely synchronous feature, if exploited, would lead to better and scaling parallel performance. Asynchronous problems, or asynchronous programming paradigms applied to loosely synchronous problems, typically do not have scaling parallel speedup proportional to number of nodes used.
• The easier (to use) asynchronous software paradigm led to a quicker implementation.
• The underlying target hardware could not exploit the performance gains of the loosely synchronous paradigm. For instance, a distributed computer network, such as that in Figures 3.10 or 15.2, might have latencies and bandwidth deficiences so that the asynchronous software paradigm performed as well as the loosely synchronous approach.

Thus, we see that loosely synchronous problems have an irregular underlying graph, but the underlying macroscopic synchronicity allows either the user or compiler to achieve higher performance. This is an opportunity (to achieve better performance), but also a challenge (it is not easy to exploit). Typically, asynchronous problems-or at least asynchronous problems that will get reasonable parallelism-have as much irregularity as loosely synchronous problems. However, they have larger grain size and lower communication-to-calculation ratios (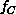 in Equation 3.10), so that one can obtain good performance without the loosely synchronous constraint. For instance, the chess tree of Figure 14.4 is more irregular and dynamic than the Barnes-Hut tree of Figure 12.11. However, the leaves of the Barnes-Hut are more tightly coupled than those of the chess tree. 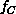In Figure 3.11(b) the satellites represent much larger grain size (and hence lower values in Equation 3.10) than the small (in computational load) finite-element nodal points in Figure 12.8 (Color Plate).

As illustrated in Figure 18.4, one must implement asynchronous levels of a problem with asynchronous software paradigms and execute on a MIMD machine. Synchronous and perhaps loosely synchronous components can be implemented with synchronous software paradigms and executed with good performance on SIMD architectures; however, one may always choose to use a more flexible software model and if necessary a more flexible hardware architecture. As we have seen, MIMD architectures support both asynchronous and the more restricted loosely synchronous class; SIMD machines support synchronous and perhaps some loosely synchronous problems. These issues are summarized in Tables 18.2 and 18.3.

  
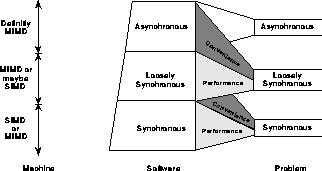
Figure 18.4: Mapping of Asynchronous, Loosely Synchronous, and Synchronous Levels or Components of Machine, Software and Problem. Each is pictured hierarchically with the asynchronous level at the top and synchronous components at lowest level. Any one of the components may be absent.

The approaches of Sections 12.4 and 12.8 exemplify the different choices that are available. In Section 12.8, Edelsohn uses an asynchronous system to control the high level of the tree with the lower levels implemented loosely synchronously for the particle dynamics  and the multigrid differential equation solver. Warren and Salmon use a loosely synchronous system at each level. Software support for such structured adaptive problems is discussed in [Choudhary:92d] as part of the plans to add support of properly loosely synchronous problems to FortranD and High Performance Fortran (HPF). 

  
Table 18.2: What is the ``correct'' machine architecture for each problem class?

In a traditional Fortran or HPF compiler, the unit of computation is the program or perhaps subroutine. Each Fortran statement (block) is executed sequentially (possibly with parallelism implied internally to statement (block) as in HPF), with synchronization at the end of each block. However, one could choose a smaller unit with loosely synchronous implementation of blocks and an overall asynchronous system for the statements (blocks). We are currently using this latter strategy for an HPF interpreter based on the MOVIE technology of Chapter 17. This again illustrates that in a hierarchical problem, one has many choices at the higher level (coarse grain) of the problem. The parallel C++ system Mentat developed by Grimshaw [Grimshaw:93b] uses similar ideas.

  
Table 18.3: Candidate Software Paradigms for each problem architecture.