




Next: 3.6 Compound Complex Systems
Up: 3 A Methodology for
Previous: 3.4 The Temporal Properties
Now we switch topics and consider the spatial properties of complex systems.
The size N of the complex system is obviously an important
property. Note that we think of a complex system as a set of members with their spatial structure evolving with time. Sometimes,
the time domain has a definite ``size'' but often one can evolve the
system indefinitely in time. However, most complex systems have a
natural spatial size with the spatial domain consisting of N
members. In the examples of Section 3.3, the seismic example
had a definite spatial extent and unlimited time domain; on the other
hand, Gaussian elimination had 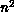 spatial members evolving for a fixed number of n ``time'' steps. As
usual, the value of spatial size N will depend on the granularity or
detail with which one looks at the complex system. One could consider
a parallel computer as a complex system constructed as a collection of
transistors with a correspondingly very large value of
spatial members evolving for a fixed number of n ``time'' steps. As
usual, the value of spatial size N will depend on the granularity or
detail with which one looks at the complex system. One could consider
a parallel computer as a complex system constructed as a collection of
transistors with a correspondingly very large value of 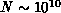 but here we will view the processor node as the fundamental entity and
define the spatial size of a parallel computer viewed as a complex
system, by the number
but here we will view the processor node as the fundamental entity and
define the spatial size of a parallel computer viewed as a complex
system, by the number 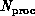 of processing nodes.
of processing nodes.
Now is a natural time to define the von Neumann complex system
spatial structure which is relevant, of course, for computer architecture. We
will formally define this to be a system with no spatial extent, i.e.
size 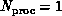 . Of course, a von Neumann node can have a
sophisticated structure if we look at fine enough resolution with multiple
functional units. More precisely, perhaps, we can generalize this complex
system to one where
. Of course, a von Neumann node can have a
sophisticated structure if we look at fine enough resolution with multiple
functional units. More precisely, perhaps, we can generalize this complex
system to one where 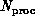 is small and will not scale up to large
values.
is small and will not scale up to large
values.
Consider mapping a seismic simulation with 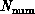 grid
points onto a parallel machine with
grid
points onto a parallel machine with 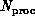 processors. An important
parameter is the grain size n of the resultant decomposition. We
can introduce the problem grain size
processors. An important
parameter is the grain size n of the resultant decomposition. We
can introduce the problem grain size 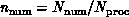 and the computer grain size
and the computer grain size  as the memory contained in each node of the parallel computer. Clearly we
must have,
as the memory contained in each node of the parallel computer. Clearly we
must have,
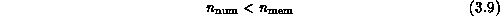
if we measure memory size in units of seismic grid points. More
interestingly, in Equation 3.10 we will relate the
performance of the parallel implementation of the seismic simulation to
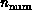 and other problem and computer characteristics. We find that,
in many cases, the parallel performance only depends on
and other problem and computer characteristics. We find that,
in many cases, the parallel performance only depends on 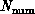 and
and
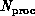 in the combination
in the combination 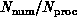 and so
grain size is a critical parameter in determining the effectiveness
of parallel computers for a particular application.
and so
grain size is a critical parameter in determining the effectiveness
of parallel computers for a particular application.
The next set of parameters describe the topology or structure of the
spatial domain associated with the complex system. The simplest parameter
of this type is the geometric dimension 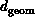 of the space. As
reviewed in Chapter 2, the original hardware and, in fact, software
(see Chapter 5) exhibited a clear geometric structure for
of the space. As
reviewed in Chapter 2, the original hardware and, in fact, software
(see Chapter 5) exhibited a clear geometric structure for
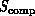 or
or 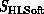 . The binary hypercube of dimension d
had this as its geometric dimension. This was an effective architecture
because it was richer than the topologies of most problems. Thus, consider
mapping a problem of dimension
. The binary hypercube of dimension d
had this as its geometric dimension. This was an effective architecture
because it was richer than the topologies of most problems. Thus, consider
mapping a problem of dimension  onto a computer of dimension
onto a computer of dimension
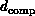 . Suppose the software system preserves the spatial structure
of the problem and that
. Suppose the software system preserves the spatial structure
of the problem and that 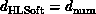 . Then, one can show
that the parallel computing overhead f has a term due to internode
communication that has the form,
. Then, one can show
that the parallel computing overhead f has a term due to internode
communication that has the form,
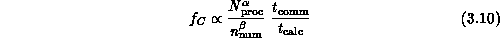
with parallel speedup S given by
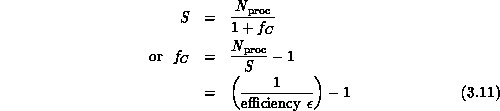
The communication overhead 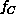 depends on the problem grain size
depends on the problem grain size
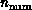 and computer complex system
and computer complex system 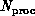 . It also involves
two parameters specifying the parallel hardware performance.
. It also involves
two parameters specifying the parallel hardware performance.
-
 : The typical time required to perform a
generic calculation. For scientific problems, this can be taken as a
floating-point calculation
: The typical time required to perform a
generic calculation. For scientific problems, this can be taken as a
floating-point calculation

-
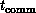 : The typical time taken to communicate
a single word between two nodes connected in the hardware topology.
: The typical time taken to communicate
a single word between two nodes connected in the hardware topology.
The definitions of 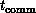 and
and  are imprecise
above. In particular,
are imprecise
above. In particular,  depends on the nature of node and
can take on very different values depending on the details of the
implementation; floating-point operations are much faster when the
operands are taken from registers than from slower parts of the memory
hierarchy. On systems built from processors like the Intel i860 chip,
these effects can be large;
depends on the nature of node and
can take on very different values depending on the details of the
implementation; floating-point operations are much faster when the
operands are taken from registers than from slower parts of the memory
hierarchy. On systems built from processors like the Intel i860 chip,
these effects can be large;  could be
could be 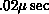 from registers (50 MFLOPS) and larger by a factor of ten when the
variables a,b are fetched from dynamic RAM. Again, communication
speed
from registers (50 MFLOPS) and larger by a factor of ten when the
variables a,b are fetched from dynamic RAM. Again, communication
speed 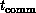 depends on internode message size (a software
characteristic) and the latency (startup time) and
bandwidth of the computer communication subsystem.
depends on internode message size (a software
characteristic) and the latency (startup time) and
bandwidth of the computer communication subsystem.
Returning to Equation 3.10, we really only need to understand
here that the term 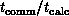 indicates that communication
overhead depends on relative performance of the internode communication
system and node (floating-point) processing unit. A real study of
parallel computer performance would require a deeper discussion of the
exact values of
indicates that communication
overhead depends on relative performance of the internode communication
system and node (floating-point) processing unit. A real study of
parallel computer performance would require a deeper discussion of the
exact values of 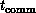 and
and  . More interesting here is
the dependence
. More interesting here is
the dependence 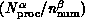 on the number of
processors
on the number of
processors 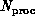 and problem grain size
and problem grain size 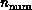 . As
described above, grain size
. As
described above, grain size 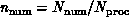 depends on both the problem and the computer. The values of
depends on both the problem and the computer. The values of  and
and 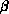 are given by
are given by
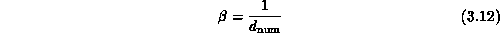
independent of computer parameters, while if
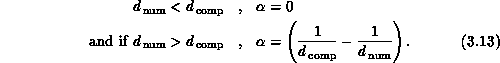
The results in Equation 3.13 quantify the penalty, in
terms of a value of 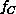 that increases with
that increases with 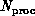 , for a
computer architecture that is less rich than the problem
architecture. An attractive feature of the
hypercube architecture is that
, for a
computer architecture that is less rich than the problem
architecture. An attractive feature of the
hypercube architecture is that 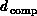 is large and one is
essentially always in the regime governed by the top line in
Equation 3.13. Recently, there has been a trend away
from rich topologies like the hypercube towards the view that the node
interconnect should be considered as a routing network or switch to be
implemented in the very best technology. The original MIMD machines
from Intel, nCUBE, and AMETEK all used
hypercube topologies, as did the SIMD Connection
Machines CM-1 and CM-2. The nCUBE-2,
introduced in 1990, still uses a hypercube topology but both it and the
second generation Intel iPSC/2 used a hardware routing that ``hides''
the hypercube connectivity. The latest Intel Paragon and Touchstone
Delta and Symult (ex-Ametek) 2010 use a two-dimensional mesh with
wormhole routing. It is not clear how to incorporate these new node
interconnects into the above picture and further research is needed.
Presumably, we would need to add new complex system properties and
perhaps generalize the definition of dimension
is large and one is
essentially always in the regime governed by the top line in
Equation 3.13. Recently, there has been a trend away
from rich topologies like the hypercube towards the view that the node
interconnect should be considered as a routing network or switch to be
implemented in the very best technology. The original MIMD machines
from Intel, nCUBE, and AMETEK all used
hypercube topologies, as did the SIMD Connection
Machines CM-1 and CM-2. The nCUBE-2,
introduced in 1990, still uses a hypercube topology but both it and the
second generation Intel iPSC/2 used a hardware routing that ``hides''
the hypercube connectivity. The latest Intel Paragon and Touchstone
Delta and Symult (ex-Ametek) 2010 use a two-dimensional mesh with
wormhole routing. It is not clear how to incorporate these new node
interconnects into the above picture and further research is needed.
Presumably, we would need to add new complex system properties and
perhaps generalize the definition of dimension 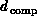 as we
will see below is in fact necessary for Equation 3.10 to
be valid for problems whose structure is not geometrically based.
as we
will see below is in fact necessary for Equation 3.10 to
be valid for problems whose structure is not geometrically based.
Returning to Equations 3.10 through 3.12,
we note that we have not properly defined the correct dimension
 or
or 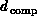 to use. We have implicitly equated
this with the natural geometric dimension but this is not
always correct. This is illustrated by the complex system
to use. We have implicitly equated
this with the natural geometric dimension but this is not
always correct. This is illustrated by the complex system 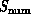 consisting of a set of particles in three dimensions interacting
with a long range force such as gravity or electrostatic charge. The
geometric structure is local with
consisting of a set of particles in three dimensions interacting
with a long range force such as gravity or electrostatic charge. The
geometric structure is local with 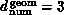 but
the complex system structure is quite different; all particles are
connected to all others. As described in Chapter 3 of [Fox:88a],
this implies that
but
the complex system structure is quite different; all particles are
connected to all others. As described in Chapter 3 of [Fox:88a],
this implies that 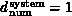 whatever the
underlying geometric structure. We define the system
dimension
whatever the
underlying geometric structure. We define the system
dimension 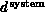 for a general complex
system to reflect the system connectivity. Consider Figure 3.9
which shows a general domain D in a complex system. We define the
volume
for a general complex
system to reflect the system connectivity. Consider Figure 3.9
which shows a general domain D in a complex system. We define the
volume 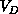 of this domain by the information in it. Mathematically,
of this domain by the information in it. Mathematically,
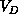 is the computational complexity needed to simulate D in isolation.
In a geometric system
is the computational complexity needed to simulate D in isolation.
In a geometric system
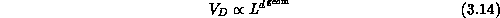
where L is a geometric length scale. The domain D is not in general
isolated and is connected to the rest of the complex system. Information
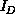 flows in D and again in a geometric system.
flows in D and again in a geometric system. 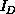 is a surface
effect with
is a surface
effect with
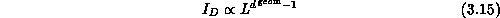
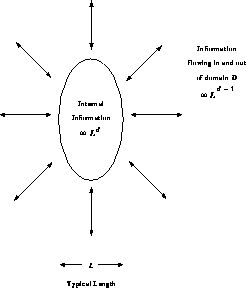
Figure 3.9: The Information Density and Flow in a General Complex System
with Length Scale L
If we view the complex system as a graph, 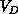 is related to the
number of links of the graph inside D and
is related to the
number of links of the graph inside D and 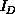 is related to the
number of links cut by the surface of D. Equations 3.14
and 3.15 are altered in cases like the long-range
force problem where the complex system
connectivity is no longer geometric. We define the system dimension to
preserve the surface versus volume interpretation of
Equation 3.15 compared to Equation 3.14.
Thus, generally we define
is related to the
number of links cut by the surface of D. Equations 3.14
and 3.15 are altered in cases like the long-range
force problem where the complex system
connectivity is no longer geometric. We define the system dimension to
preserve the surface versus volume interpretation of
Equation 3.15 compared to Equation 3.14.
Thus, generally we define
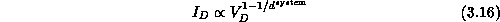
With this definition of system dimension 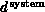 , we will
find that Equations 3.10 through 3.12
essentially hold in general. In particular for the long range force problem,
one finds
, we will
find that Equations 3.10 through 3.12
essentially hold in general. In particular for the long range force problem,
one finds 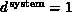 independent of
independent of 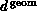 .
.
A very important special type of spatial structure is the case
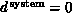 when we find the embarrassingly
parallel or spatially
disconnected complex system. Here there is no connection between
the different members in the spatial domain. Applying this to parallel
computing, we see that if
when we find the embarrassingly
parallel or spatially
disconnected complex system. Here there is no connection between
the different members in the spatial domain. Applying this to parallel
computing, we see that if 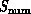 or
or 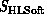 is
spatially disconnected, then it can be parallelized very straightforwardly.
In particular, any MIMD machine can be used whatever the temporal
structure of the complex system. SIMD machines can only be used to
simulate embarrassingly parallel complex systems which have spatially
disconnected members with identical structure.
is
spatially disconnected, then it can be parallelized very straightforwardly.
In particular, any MIMD machine can be used whatever the temporal
structure of the complex system. SIMD machines can only be used to
simulate embarrassingly parallel complex systems which have spatially
disconnected members with identical structure.
In Section 13.7, we extend the analysis of this section to cover
the performance of hierarchical memory
machines. We find that one needs to replace subdomains in space with
those in space-time.
In Chapter 11, we describe other interesting spatial properties
in terms of a particle analogy. We find system temperature and phase
transitions as one heats and cools the complex system.





Next: 3.6 Compound Complex Systems
Up: 3 A Methodology for
Previous: 3.4 The Temporal Properties
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
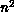 spatial members evolving for a fixed number of n ``time'' steps. As
usual, the value of spatial size N will depend on the granularity or
detail with which one looks at the complex system. One could consider
a parallel computer as a complex system constructed as a collection of
transistors with a correspondingly very large value of
spatial members evolving for a fixed number of n ``time'' steps. As
usual, the value of spatial size N will depend on the granularity or
detail with which one looks at the complex system. One could consider
a parallel computer as a complex system constructed as a collection of
transistors with a correspondingly very large value of 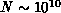 but here we will view the processor node as the fundamental entity and
define the spatial size of a parallel computer viewed as a complex
system, by the number
but here we will view the processor node as the fundamental entity and
define the spatial size of a parallel computer viewed as a complex
system, by the number 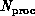 of processing nodes.
of processing nodes.





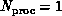 . Of course, a von Neumann node can have a
sophisticated structure if we look at fine enough resolution with multiple
functional units. More precisely, perhaps, we can generalize this complex
system to one where
. Of course, a von Neumann node can have a
sophisticated structure if we look at fine enough resolution with multiple
functional units. More precisely, perhaps, we can generalize this complex
system to one where 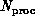 is small and will not scale up to large
values.
is small and will not scale up to large
values.
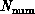 grid
points onto a parallel machine with
grid
points onto a parallel machine with 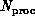 processors. An important
parameter is the grain size n of the resultant decomposition. We
can introduce the problem grain size
processors. An important
parameter is the grain size n of the resultant decomposition. We
can introduce the problem grain size 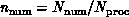 and the computer grain size
and the computer grain size  as the memory contained in each node of the parallel computer. Clearly we
must have,
as the memory contained in each node of the parallel computer. Clearly we
must have,
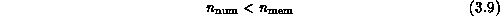
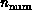 and other problem and computer characteristics. We find that,
in many cases, the parallel performance only depends on
and other problem and computer characteristics. We find that,
in many cases, the parallel performance only depends on 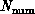 and
and
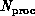 in the combination
in the combination 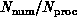 and so
grain size is a critical parameter in determining the effectiveness
of parallel computers for a particular application.
and so
grain size is a critical parameter in determining the effectiveness
of parallel computers for a particular application.
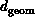 of the space. As
reviewed in Chapter
of the space. As
reviewed in Chapter 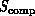 or
or 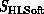 . The binary hypercube of dimension d
had this as its geometric dimension. This was an effective architecture
because it was richer than the topologies of most problems. Thus, consider
mapping a problem of dimension
. The binary hypercube of dimension d
had this as its geometric dimension. This was an effective architecture
because it was richer than the topologies of most problems. Thus, consider
mapping a problem of dimension  onto a computer of dimension
onto a computer of dimension
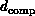 . Suppose the software system preserves the spatial structure
of the problem and that
. Suppose the software system preserves the spatial structure
of the problem and that 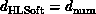 . Then, one can show
that the parallel computing overhead f has a term due to internode
communication that has the form,
. Then, one can show
that the parallel computing overhead f has a term due to internode
communication that has the form,
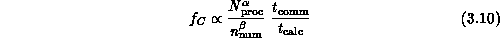
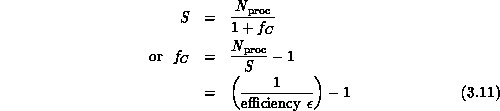
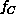 depends on the problem grain size
depends on the problem grain size
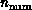 and computer complex system
and computer complex system 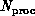 . It also involves
two parameters specifying the parallel hardware performance.
. It also involves
two parameters specifying the parallel hardware performance.
 : The typical time required to perform a
generic calculation. For scientific problems, this can be taken as a
floating-point calculation
: The typical time required to perform a
generic calculation. For scientific problems, this can be taken as a
floating-point calculation

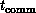 : The typical time taken to communicate
a single word between two nodes connected in the hardware topology.
: The typical time taken to communicate
a single word between two nodes connected in the hardware topology.
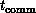 and
and  are imprecise
above. In particular,
are imprecise
above. In particular,  depends on the nature of node and
can take on very different values depending on the details of the
implementation; floating-point operations are much faster when the
operands are taken from registers than from slower parts of the memory
hierarchy. On systems built from processors like the Intel i860 chip,
these effects can be large;
depends on the nature of node and
can take on very different values depending on the details of the
implementation; floating-point operations are much faster when the
operands are taken from registers than from slower parts of the memory
hierarchy. On systems built from processors like the Intel i860 chip,
these effects can be large;  could be
could be 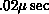 from registers (50 MFLOPS) and larger by a factor of ten when the
variables a,b are fetched from dynamic RAM. Again, communication
speed
from registers (50 MFLOPS) and larger by a factor of ten when the
variables a,b are fetched from dynamic RAM. Again, communication
speed 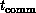 depends on internode message size (a software
characteristic) and the latency
depends on internode message size (a software
characteristic) and the latency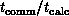 indicates that communication
overhead depends on relative performance of the internode communication
system and node (floating-point) processing unit. A real study of
parallel computer performance would require a deeper discussion of the
exact values of
indicates that communication
overhead depends on relative performance of the internode communication
system and node (floating-point) processing unit. A real study of
parallel computer performance would require a deeper discussion of the
exact values of 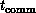 and
and  . More interesting here is
the dependence
. More interesting here is
the dependence 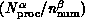 on the number of
processors
on the number of
processors 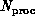 and problem grain size
and problem grain size 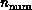 . As
described above, grain size
. As
described above, grain size 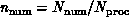 depends on both the problem and the computer. The values of
depends on both the problem and the computer. The values of  and
and 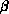 are given by
are given by
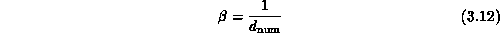
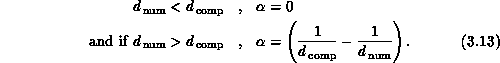
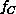 that increases with
that increases with 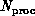 , for a
computer architecture that is less rich than the problem
architecture.
, for a
computer architecture that is less rich than the problem
architecture.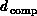 is large and one is
essentially always in the regime governed by the top line in
Equation
is large and one is
essentially always in the regime governed by the top line in
Equation 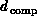 as we
will see below is in fact necessary for Equation
as we
will see below is in fact necessary for Equation  or
or 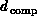 to use. We have implicitly equated
this with the natural geometric dimension but this is not
always correct. This is illustrated by the complex system
to use. We have implicitly equated
this with the natural geometric dimension but this is not
always correct. This is illustrated by the complex system 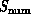 consisting of a set of particles in three dimensions interacting
with a long range force such as gravity or electrostatic charge. The
geometric structure is local with
consisting of a set of particles in three dimensions interacting
with a long range force such as gravity or electrostatic charge. The
geometric structure is local with 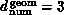 but
the complex system structure is quite different; all particles are
connected to all others. As described in Chapter 3 of [
but
the complex system structure is quite different; all particles are
connected to all others. As described in Chapter 3 of [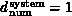 whatever the
underlying geometric structure. We define the system
dimension
whatever the
underlying geometric structure. We define the system
dimension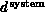 for a general complex
system to reflect the system connectivity. Consider Figure
for a general complex
system to reflect the system connectivity. Consider Figure 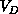 of this domain by the information in it. Mathematically,
of this domain by the information in it. Mathematically,
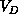 is the computational complexity needed to simulate D in isolation.
In a geometric system
is the computational complexity needed to simulate D in isolation.
In a geometric system
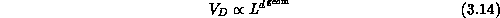
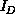 flows in D and again in a geometric system.
flows in D and again in a geometric system. 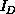 is a surface
effect with
is a surface
effect with
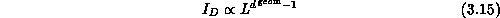

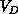 is related to the
number of links of the graph inside D and
is related to the
number of links of the graph inside D and 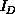 is related to the
number of links cut by the surface of D. Equations
is related to the
number of links cut by the surface of D. Equations 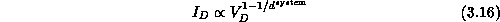
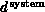 , we will
find that Equations
, we will
find that Equations 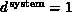 independent of
independent of 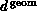 .
.
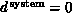 when we find the embarrassingly
parallel
when we find the embarrassingly
parallel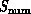 or
or  is
spatially disconnected, then it can be parallelized very straightforwardly.
In particular, any MIMD machine can be used whatever the temporal
structure of the complex system. SIMD machines can only be used to
simulate embarrassingly parallel complex systems which have spatially
disconnected members with identical structure.
is
spatially disconnected, then it can be parallelized very straightforwardly.
In particular, any MIMD machine can be used whatever the temporal
structure of the complex system. SIMD machines can only be used to
simulate embarrassingly parallel complex systems which have spatially
disconnected members with identical structure.