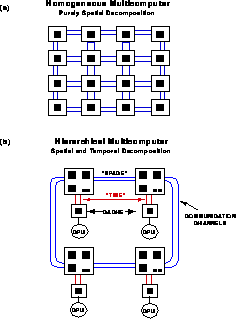
Figure 13.18: Homogeneous and Hierarchical-Memory Multicomputers. The black box represents the data that fit into the lowest level of the memory hierarchy.





In this section, we review some ideas of Fox, dating from 1987, that unify the decomposition methodologies for hierarchical- and distributed-memory computers [Fox:87b]. For a modern workstation, the hierarchical memory is formed by the cache and main memory. One needs to minimize the cache misses to ensure that, as far as possible, we reference data in cache and not in main memory. This is often referred to as the need for ``data locality.'' This term makes clear the analogy with distributed-memory parallel computers. As shown in this book, we need data locality in the latter case to avoid communications between processors. We put the discussion in this chapter because we anticipate an important application of these ideas to data-parallel Fortran. The directives in High Performance Fortran essentially specify data locality and we believe that an HPF compiler can use the concepts of this section to optimize cache use on hierarchical-memory machines. Thus, HPF and similar data-parallel languages will give better performance than conventional Fortran 77 compilers on all high-performance computers, not just parallel machines.

Figure 13.18: Homogeneous and Hierarchical-Memory Multicomputers. The
black box represents the data that fit into the lowest level of the
memory hierarchy.
Figures 13.18 and 13.19 contrast distributed-memory multicomputers, shared-memory, and sequential hierarchical-memory computers. In each case, we denote by a black square the amount of data which can fit into the lowest level of the memory hierarchy. In machines such as the nCUBE-1,2 with a simple node, illustrated in Figure 13.18(a), this amount is just what can fit into the node of the distributed-memory computers. In the other architectures shown in Figures 13.18 and 13.19, the data corresponding to the black square represents what can fit into the cache. There is one essential difference between cache and distributed memory. Both need data locality, but in the parallel case the basic data is static and fetches additional information as necessary. This gives the familiar surface-over-volume communication overheads of Equation 3.10. However, in the case of a cache, all the data must stream through it and not just the data needed to provide additional information. For distributed-memory machines, we minimize the need for information flow into and out of a grain as shown in Figure 3.9. For hierarchical-memory machines, we need to maximize the number of times we access the data in cache. These are related but not identical concepts which we will now compare. We can use the space-time complex system language introduced in Chapter 3.
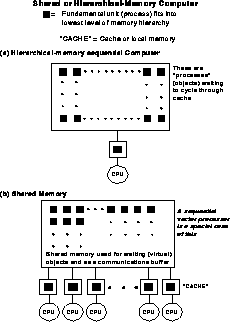
Figure 13.19: Shared Hierarchical-Memory Computers. ``Cache'' could either
be a time cache or local (software-controlled) memory.
Figure 13.20 introduces a new time constant, 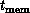 , which is contrasted with
, which is contrasted with 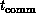 and
and  introduced in Section 3.5. The constant
introduced in Section 3.5. The constant 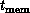 represents the
time it takes to load a word into cache. As shown in this figure, the
cache overhead is also a ``surface-over-volume'' effect just as it was
in Section 3.5, but now the surface is measured in the
temporal direction and the volume is that of a domain in space and
time. We find
represents the
time it takes to load a word into cache. As shown in this figure, the
cache overhead is also a ``surface-over-volume'' effect just as it was
in Section 3.5, but now the surface is measured in the
temporal direction and the volume is that of a domain in space and
time. We find 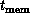 , time, and memory hierarchy are analogous
to
, time, and memory hierarchy are analogous
to 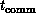 , space, and distributed memory.
, space, and distributed memory.
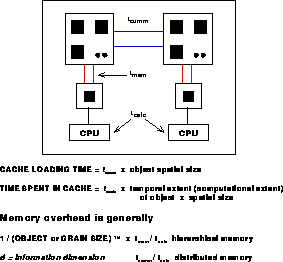
Figure: The Fundamental Time Constants of a Node. The information
dimension represented by d is discussed in Section 3.5.
Space-time decompositions are illustrated in Figure 13.21 for a simple one-dimensional problem. The decomposition in Figure 13.21(a) is fine for distributed-memory machines, but has poor cache performance. It is blocked in space but not in time. The optimal decompositions are ``space-time'' blocked and illustrated in Figure 13.21(b) and (c).
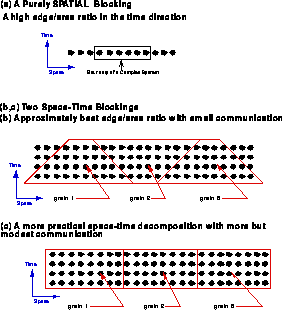
Figure 13.21: Decompositions for a simple one-dimensional wave equation.
A ``space-time'' blocking is a universal high-performance implementation of data locality. It will lead to good performance on both distributed- and hierarchical-memory machines. This is best known for the use of the BLAS-3 matrix-matrix primitives in LAPACK and other matrix library projects (see Section 8.1) [Demmel:91a]. The next step is to generate such optimal decompositions from a High Performance Fortran compiler.
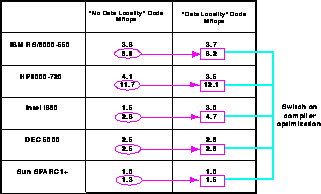
Figure 13.22: Performance of a Random Surface Fortran Code on Five RISC
Architecture Sequential Computers. The optimizations are described in
the text.
We can illustrate these ideas with the application of Section 7.2 [Coddington:93a]. Table 7.1 records performance of the original code used, but this C version was improved by an order of magnitude in performance in a carefully rewritten Fortran code. The relevance of data locality for this new code is shown in Figure 13.22. For each of a set of five RISC processors, we show four performance numbers gotten by switching on and off ``system Fortran compiler optimization'' and ``data locality.'' As seen from Section 7.2, this application is naturally very irregular and normal data structures do not express this locality and preserve it. Even if one starts with neighboring points in the simulated space, ``near'' each other also in the computer, this is not easily preserved by the dynamic retriangulation. In the ``data locality'' column, we have arranged storage to preserve locality as far as possible; neighboring physical points are stored near each other in memory. A notable feature of Figure 13.22 is that the Intel i860 shows the largest improvement from forcing data locality-even after compilation optimization, this action improves performance by 70%. A similar result was found in [Das:92c] for an unstructured mesh partial differential equation solver. Other architectures such as the HP9000-720 with large caches show smaller effects. In Figure 13.22, locality was achieved by user manipulation-as discussed, a next step is to put such intelligence in parallel compilers.




