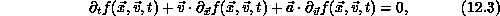
Continuous physical systems must generally be ``discretized'' prior to analysis with a digital computer. In practice, there are relatively few ways to discretize a physical system. Finite-element and finite-difference approximations are useful for dealing with partial differential equations in a small number of dimensions (up to three). If the dimensionality of the independent variable space is large, however, discretization by finite difference or finite elements becomes unwieldy. For example, the collisionless Boltzman equation,
is expressed as a partial differential equation in six independent variables.
A fairly modest discretization of the domain with 100 ``elements'' in each
dimension would result in a system with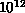 
elements. A simulation of
this size is out of the question on computers which will be available in the
foreseeable future.
Fortunately, another means of discretization is available. Particle Simulation (or N-body simulation) is discussed at length by Hockney and Eastwood [Hockney:81a]. It is appropriate for systems like the collisionless and collisional Boltzman equation, and hence it is applicable to a number of outstanding problems in astrophysics , where the basic physical processes are governed by Newtonian gravity and the Boltzman equation [Binney:87a].
In such simulations, the phase-space density, f, is represented by a swarm of ``particles'', or ``bodies'' which evolve in time according to the dynamics of Newtonian gravity:
The 3N second-order, ordinary differential equations may be integrated in time by a large number of
methods, ranging from the very simple (Euler's method) to the very
complex [Aarseth:85a]. The difficulty with using
Equation 12.4 is that a straightforward implementation of
the right-hand sides of these equations requires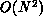 
operations.
Each of N accelerations is the vector sum of N-1 components, each
of which requires a handful of floating-point operations (including at
least one square-root). Even if one utilizes Newton's second law, one
can cut the total number of operations by half, but the asymptotic
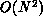behavior remains unchanged. N-body simulations using direct
summation are practical up to a few tens of thousands of bodies on
modern supercomputers. Even the teraflop performance
promised by parallel computation would only increase this by an order
of magnitude or so. Substantially larger simulations require
alternative methods for evaluating the forces. The fact that gravity
is ``long-range,'' makes rapid evaluation of the forces problematical.
It is not acceptable to simply disregard all bodies beyond a certain
fixed cutoff, because the contribution of distant bodies does not
decrease fast enough to balance the fact that the number of bodies at a
given distance is an increasing function of distance.
Recent algorithmic advances [Appel:85a], [Barnes:86a], [Greengard:87b], [Jernighan:89a] however, have shown that while it is not acceptable to disregard distant collections of bodies, it is possible to accurately approximate their contribution without summing all of the individual components. It has been known since the time of Newton that the effect of the earth on an apple may be computed by replacing the countless individual atoms in the earth with a single point-mass located at the earth's center. The force calculation is then:
