




Next: 12.4.5 Comments on Performance
Up: 12.4 Tree Codes for
Previous: 12.4.3 Parallelism in Tree
Many parallel algorithms conform to a pattern of activity that
can loosely be described as:
- Choose a decomposition-that is, determine which processor is responsible
for updating which data.
- Communicate-that is, arrange for some data to reside in several
processors. Exactly which data are replicated, and how they are stored
depends on the next phase.
- Proceed with calculation using an essentially serial
implementation, but restrict the data updated by each processor to
those in the processor's domain.
In this volume, the techniques discussed are structured in this way. Some
important advantages arise from this approach to parallelism. It leads to
modularity and portability, by separating distinct functions into separate
phases. It also allows reuse of sequential code (in the third phase), which
is frequently highly optimized and extensively tested. One drawback of this
approach is the fact that it precludes overlapping of communication
and calculation. We shall not be concerned with overlap of communication and
calculation because communication overhead constitutes a small part of the
overall time in parallel tree code implementations [Salmon:90a].
We have already discussed decomposition, and described the use of
orthogonal recursive bisection to determine processor domains. The
next step is the acquisition of ``locally essential data'', that is, the
data that will be needed to compute the forces on the bodies in a local
domain. In other applications one finds that the locally essential
data associated with a domain is itself local. That is, it comes
from a limited region surrounding the processor domain. In the case of
hierarchical N-body simulations, however, the locally essential data is
not restricted to a particular region of space. Nevertheless, the
hierarchical nature of the algorithm guarantees that if a processor's
domain is spatially limited, then any particle within that domain will
not require detailed information about the particle distribution in
distant regions of space. This idea is illustrated in
Figure 12.14, which shows the parts of the tree that are
required to compute forces on bodies in the grey region. Clearly, the
locally essential data for a limited domain is much smaller than the
total data set (shown in Figure 12.11). In fact, when the
grain size of the domain is large, that is, when the number of bodies in
the domain is large, the size of the locally essential data set is only
a modest constant factor larger than the local data set itself
[Salmon:90a]. This means that the work (both communication and
additional computation) required to obtain and assemble the locally
essential dataset is proportional to the grain size, that is, is
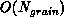 . In contrast, the work required to compute the forces
in parallel is
. In contrast, the work required to compute the forces
in parallel is 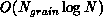 . The ``big-O'' notation can hide
large constants which dominate practical considerations. Typical
astrophysical simulations with
. The ``big-O'' notation can hide
large constants which dominate practical considerations. Typical
astrophysical simulations with 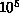 -
-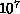 bodies perform
200500 interactions per body [Hernquist:87a],
[Warren:92a], and each interaction costs from 30 to 60 floating-point
operations. Thus, there is reason to be optimistic that assembly
of the locally essential data set will not be prohibitively expensive.
bodies perform
200500 interactions per body [Hernquist:87a],
[Warren:92a], and each interaction costs from 30 to 60 floating-point
operations. Thus, there is reason to be optimistic that assembly
of the locally essential data set will not be prohibitively expensive.

Figure 12.14: The Locally Essential Data Needed to Compute Forces in a
Processor Domain, Located in the Lower Left Corner of the System
Determining, in parallel, which data is locally essential for which
processors is a formidable task. Two facts allow us to organize the
communication of data into a regular pattern that guarantees that each
processor receives precisely the locally essential data which it needs.
- At each level of the orthogonal recursive bisection, the domains are
always rectangles.
- It is possible to quickly determine whether a given cell's multipole
approximation is acceptable for all particles in a given rectangular domain.
Or, conversely, whether the locally essential data for the domain includes
information contained in the daughters of the given cell. This test is
called the domain multipole acceptability criterion (DMAC).
The procedure by which processors go from having only local data to having
all locally essential data consists of a loop over each of the bisections in
the ORB tree. To initialize the iteration, each processor builds a tree from
its local data. Then, for each bisector, it traverses its tree, applying the
DMAC at each node, using the complimentary domain as an argument,
that is, asking whether the given cell contains an approximation that is
sufficient for all bodies in the domain on the other side of the current ORB
bisector. If the DMAC succeeds, the cell is needed on the other side of the
domain, so it is copied to a buffer and queued for transmission. Traversal
of the current branch can stop at this point because no additional
information within the current branch of the local tree can possibly be
necessary on the other side of the bisector. If the DMAC fails, traversal
continues to deeper levels of the tree. This procedure is shown
schematically in code in Table 12.1.

Table 12.1: Outline of BuildLETree which constructs a locally essential
representation of a tree.
Figure 12.15 shows schematically how some data might travel around
a 16-processor system during execution of the above code.
The second tree traversal in the above code conserves a processor's memory by
reclaiming data which was transmitted through the processor, but which is not
needed by the processor itself, or any other member of its current subset.
In Figure 12.15, the body sent from processor 0110 through 1110
and 1010 to 1011 would likely be deleted from processor 1110's tree during
the pruning on channel 2, and from 1010's tree during the pruning on
channel 0.
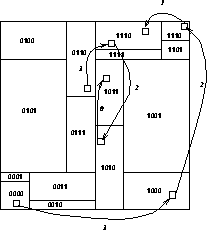
Figure 12.15: Data Flow in a 16 Processor System. Arrows indicate the flow of
data and are numbered with a decreasing ``channel'' number corresponding to
the bisector being traversed.
The Code requires the existence of a DMAC function. Obviously, the DMAC
depends on the details of the MAC which will eventually be used to traverse
the tree to evaluate forces. Notice, however, that the DMAC must be
evaluated before the entire contents of a cell are available in a
particular processor. (This happens whenever the cell itself extends outside
of the processor's domain). Thus, the DMAC must rely on purely geometric
criteria (the size and location of the cell), and cannot depend on, for
example, the
exact location of the center-of-mass of the cell. The DMAC is allowed,
however, to err on the side of caution. That is, it is allowed to return a
negative result about a cell even though subsequent data may reveal that the
cell is indeed acceptable. The penalty for such ``false negatives'' is
degraded performance, as they cause data to be unnecessarily communicated and
assembled into locally essential data sets.
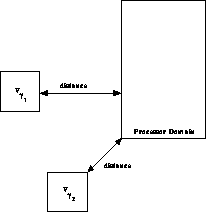
Figure 12.16: The Distance Used by the DMAC is Computed by Finding the Shortest
Distance Between the Processor Domain and the Boundary of the Cell.
Because the DMAC must work with considerably less information than the
MAC, it is somewhat easier to categorically describe its behavior.
Figure 12.16 shows schematically how the DMAC is
implemented. Recall that the MAC is based on a ``distance-to-size''
ratio. The distance used by the DMAC is the shortest distance from the
cell to the processor domain. The ``min-distance'' MAC
[Salmon:90a;92a] uses precisely
this distance to decide whether a multipole approximation is
acceptable. Thus, in a sense, the min-distance MAC is best suited to
parallelization because it is equivalent to its own DMAC. The DMAC
generates fewer false-positive decisions. Fortunately, the
min-distance MAC also resolves certain difficulties associated with
more commonly used MACs, and is arguably the best of the ``simple''
MACs [Salmon:92a].





Next: 12.4.5 Comments on Performance
Up: 12.4 Tree Codes for
Previous: 12.4.3 Parallelism in Tree
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
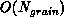 . In contrast, the work required to compute the forces
in parallel is
. In contrast, the work required to compute the forces
in parallel is 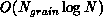 . The ``big-O'' notation can hide
large constants which dominate practical considerations. Typical
astrophysical simulations with
. The ``big-O'' notation can hide
large constants which dominate practical considerations. Typical
astrophysical simulations with 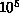 -
-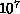 bodies perform
200500 interactions per body [Hernquist:87a],
[Warren:92a], and each interaction costs from 30 to 60 floating-point
operations. Thus, there is reason to be optimistic that assembly
of the locally essential data set will not be prohibitively expensive.
bodies perform
200500 interactions per body [Hernquist:87a],
[Warren:92a], and each interaction costs from 30 to 60 floating-point
operations. Thus, there is reason to be optimistic that assembly
of the locally essential data set will not be prohibitively expensive.








