




Next: 4.3.7 QCD on the
Up: 4.3 Quantum Chromodynamics
Previous: 4.3.5 Concurrent QCD Machines
To make good use of MIMD distributed-memory machines like hypercubes, one
should employ domain decomposition. That is, the domain of the problem
should be divided into subdomains of equal size, one for each processor in
the hypercube; and communication routines should be written to take care of
data transfer across the processor boundaries. Thus, for a lattice
calculation, the N sites are distributed among the 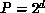 processors
using a decomposition that ensures that processors assigned to adjacent
subdomains are directly linked by a communication channel in the hypercube
topology. Each processor then independently works through its subdomain of
processors
using a decomposition that ensures that processors assigned to adjacent
subdomains are directly linked by a communication channel in the hypercube
topology. Each processor then independently works through its subdomain of
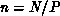 sites, updating each one in turn, and only communicating with
neighboring processors when doing boundary sites. This communication
enforces ``loose synchronization,'' which
stops any one processor from racing ahead of the others. Load
balancing is achieved with equal-size domains. If the nodes contain at
least two sites of the lattice, all the nodes can update in parallel,
satisfying detailed balance, since loose
synchronicity guarantees that all nodes will be doing black, then red
sites alternately.
sites, updating each one in turn, and only communicating with
neighboring processors when doing boundary sites. This communication
enforces ``loose synchronization,'' which
stops any one processor from racing ahead of the others. Load
balancing is achieved with equal-size domains. If the nodes contain at
least two sites of the lattice, all the nodes can update in parallel,
satisfying detailed balance, since loose
synchronicity guarantees that all nodes will be doing black, then red
sites alternately.
The characteristic timescale of the communication, 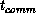 , corresponds
roughly to the time taken to transfer a single
, corresponds
roughly to the time taken to transfer a single 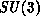 matrix from one node to
its neighbor. Similarly, we can characterize the calculational part of the
algorithm by a timescale,
matrix from one node to
its neighbor. Similarly, we can characterize the calculational part of the
algorithm by a timescale, 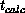 , which is roughly the time taken to
multiply together two
, which is roughly the time taken to
multiply together two 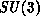 matrices. For all hypercubes built without floating-point accelerator chips,
matrices. For all hypercubes built without floating-point accelerator chips, 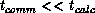 and, hence,
QCD simulations are extremely ``efficient,'' where efficiency
and, hence,
QCD simulations are extremely ``efficient,'' where efficiency  (Equations 3.10 and 3.11) is defined by
the relation
(Equations 3.10 and 3.11) is defined by
the relation
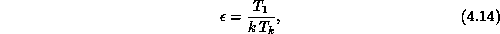
where 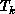 is the time taken for k processors to perform the given
calculation. Typically, such calculations have efficiencies in the range
is the time taken for k processors to perform the given
calculation. Typically, such calculations have efficiencies in the range
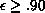 , which means they are ideally suited to this type of
computation since doubling the number of processors nearly halves the
total computational time required for solution. However, as we shall see
(for the Mark IIIfp hypercube, for example), the picture changes dramatically
when fast floating-point chips are used; then
, which means they are ideally suited to this type of
computation since doubling the number of processors nearly halves the
total computational time required for solution. However, as we shall see
(for the Mark IIIfp hypercube, for example), the picture changes dramatically
when fast floating-point chips are used; then 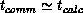 and
one must take some care in coding to obtain maximum performance.
and
one must take some care in coding to obtain maximum performance.
Rather than describe every calculation done on the Caltech hypercubes,
we shall concentrate on one calculation that has been done several times
as the machine evolved-the heavy quark potential
calculation (``heavy'' because the quenched approximation is used).
QCD provides an explanation of why quarks are confined inside hadrons, since
lattice calculations reveal that the inter-quark potential rises linearly as
the separation between the quarks increases. Thus, the attractive force
(the derivative of the potential) is independent of the separation,
unlike other forces, which usually decrease rapidly with distance. This
force, called the ``string tension,'' is carried by the gluons, which form a
kind of ``string'' between the quarks. On the other hand, at short distances,
quarks and gluons are
``asymptotically free'' and behave like electrons and photons, interacting
via a Coulomb-like force. Thus, the quark potential V is written as
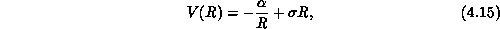
where R is the separation of the quarks,  is the coefficient of the
Coulombic potential and
is the coefficient of the
Coulombic potential and  is the string tension. In fitting
experimental charmonium data to this Coulomb plus linear potential, Eichten
et al. [Eichten:80a] estimated that
is the string tension. In fitting
experimental charmonium data to this Coulomb plus linear potential, Eichten
et al. [Eichten:80a] estimated that 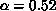 and
and
 =0.18GeV
=0.18GeV . Thus, a goal of the lattice calculations is to
reproduce these numbers. Enroute to this goal, it is necessary to show that
the numbers from the lattice are ``scaling,'' that is, if one calculates a
physical observable on lattices with different spacings then one gets the
same answer. This means that the artifacts due to the finiteness of the
lattice spacing have disappeared and continuum physics can be extracted.
. Thus, a goal of the lattice calculations is to
reproduce these numbers. Enroute to this goal, it is necessary to show that
the numbers from the lattice are ``scaling,'' that is, if one calculates a
physical observable on lattices with different spacings then one gets the
same answer. This means that the artifacts due to the finiteness of the
lattice spacing have disappeared and continuum physics can be extracted.
The first heavy quark potential calculation using a Caltech hypercube was
performed on the 64-node Mark I in 1984 on a 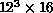 lattice with
lattice with
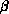 ranging from
ranging from 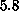 to
to 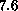 [Otto:84a]. The value of
[Otto:84a]. The value of
 was found to be
was found to be 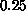 and the string tension (converting to
the dimensionless ratio)
and the string tension (converting to
the dimensionless ratio) 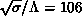 . The numbers
are quite a bit off from the charmonium data but the string tension did
appear to be scaling, albeit in the narrow window
. The numbers
are quite a bit off from the charmonium data but the string tension did
appear to be scaling, albeit in the narrow window 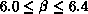 .
.
The next time around, in 1986, the 128-node Mark II hypercube was used on a
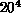 lattice with
lattice with 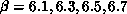 [Flower:86b]. The
dimensionless string tension decreased somewhat to 83, but clear violations
of scaling were observed: The lattice was still too coarse to see continuum
physics.
[Flower:86b]. The
dimensionless string tension decreased somewhat to 83, but clear violations
of scaling were observed: The lattice was still too coarse to see continuum
physics.
Therefore, the last (1989) calculation using the Caltech/JPL 32-node
Mark IIIfp hypercube concentrated on one 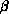 value,
value, 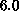 , and
investigated different lattice sizes:
, and
investigated different lattice sizes: 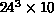 ,
, 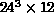 ,
, 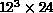 ,
, 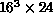 [Ding:90b]. Scaling was not
investigated; however, the values of
[Ding:90b]. Scaling was not
investigated; however, the values of 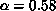 and
and
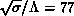 , that is,
, that is,  = 0.15GeV
= 0.15GeV ,
compare favorably with the charmonium data. This work is based on
about 1300 CPU hours on the 32-node Mark IIIfp hypercube, which has a
performance of roughly twice a CRAY X-MP processor. The
whole 128-node machine performs at
,
compare favorably with the charmonium data. This work is based on
about 1300 CPU hours on the 32-node Mark IIIfp hypercube, which has a
performance of roughly twice a CRAY X-MP processor. The
whole 128-node machine performs at 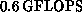 . As each node
runs at
. As each node
runs at 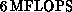 , this corresponds to a speedup of 100, and
hence, an efficiency of 78 percent. These figures are for the most
highly optimized code. The original version of the code written in C
ran on the Motorola chips at
, this corresponds to a speedup of 100, and
hence, an efficiency of 78 percent. These figures are for the most
highly optimized code. The original version of the code written in C
ran on the Motorola chips at 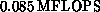 and on the Weitek
chips at
and on the Weitek
chips at 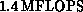 . The communication time, which is roughly
the same for both, is less than a 2 percent overhead for the former but
nearly 30 percent for the latter. When the computationally intensive
parts of the calculation are written in assembly code for the Weitek,
this overhead becomes almost 50 percent. This
. The communication time, which is roughly
the same for both, is less than a 2 percent overhead for the former but
nearly 30 percent for the latter. When the computationally intensive
parts of the calculation are written in assembly code for the Weitek,
this overhead becomes almost 50 percent. This  of
communication, shown in lines two and three in Table 4.4, is
dominated by the hardware/software message startup overhead
(latency), because for the Mark IIIfp the node-to-node
communication time,
of
communication, shown in lines two and three in Table 4.4, is
dominated by the hardware/software message startup overhead
(latency), because for the Mark IIIfp the node-to-node
communication time, 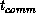 , is given by
, is given by
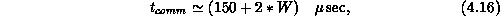
where W is the number of words transmitted. To speed up the
communication, we update all even (or odd) links (eight in our case) in
each node, allowing us to transfer eight matrix products at a time,
instead of just sending one in each message. This reduces the  by a factor of
by a factor of
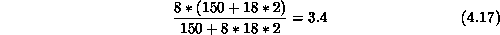
to 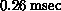 . On all hypercubes with fast floating-point
chips-and on most hypercubes without these chips for less
computationally intensive codes-such ``vectorization'' of
communication is often important. In Figure 4.10, the
speedups for many different lattice sizes are shown. For the largest
lattice size, the speedup is 100 on the 128-node machine. The speedup
is almost linear in number of nodes. As the total lattice volume
increases, the speedup increases, because the ratio of
calculation/communication increases. For more information on this
performance analysis,
see [Ding:90c].
. On all hypercubes with fast floating-point
chips-and on most hypercubes without these chips for less
computationally intensive codes-such ``vectorization'' of
communication is often important. In Figure 4.10, the
speedups for many different lattice sizes are shown. For the largest
lattice size, the speedup is 100 on the 128-node machine. The speedup
is almost linear in number of nodes. As the total lattice volume
increases, the speedup increases, because the ratio of
calculation/communication increases. For more information on this
performance analysis,
see [Ding:90c].
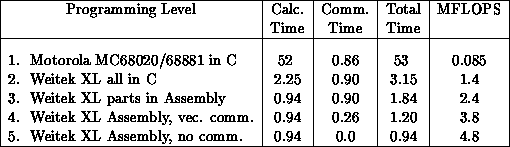
Table 4.4: Link Update Time (msec) on Mark IIIfp Node for Various Levels
of Programming
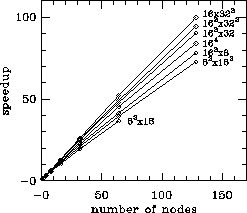
Figure 4.10: Speedups for QCD on the Mark IIIfp





Next: 4.3.7 QCD on the
Up: 4.3 Quantum Chromodynamics
Previous: 4.3.5 Concurrent QCD Machines
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
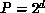 processors
using a decomposition that ensures that processors assigned to adjacent
subdomains are directly linked by a communication channel in the hypercube
topology. Each processor then independently works through its subdomain of
processors
using a decomposition that ensures that processors assigned to adjacent
subdomains are directly linked by a communication channel in the hypercube
topology. Each processor then independently works through its subdomain of
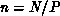 sites, updating each one in turn, and only communicating with
neighboring processors when doing boundary sites. This communication
enforces ``loose synchronization,'' which
stops any one processor from racing ahead of the others. Load
balancing is achieved with equal-size domains. If the nodes contain at
least two sites of the lattice, all the nodes can update in parallel,
satisfying detailed balance, since loose
synchronicity guarantees that all nodes will be doing black, then red
sites alternately.
sites, updating each one in turn, and only communicating with
neighboring processors when doing boundary sites. This communication
enforces ``loose synchronization,'' which
stops any one processor from racing ahead of the others. Load
balancing is achieved with equal-size domains. If the nodes contain at
least two sites of the lattice, all the nodes can update in parallel,
satisfying detailed balance, since loose
synchronicity guarantees that all nodes will be doing black, then red
sites alternately.





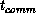 , corresponds
roughly to the time taken to transfer a single
, corresponds
roughly to the time taken to transfer a single 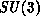 matrix from one node to
its neighbor. Similarly, we can characterize the calculational part of the
algorithm by a timescale,
matrix from one node to
its neighbor. Similarly, we can characterize the calculational part of the
algorithm by a timescale, 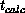 , which is roughly the time taken to
multiply together two
, which is roughly the time taken to
multiply together two 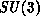 matrices. For all hypercubes built without floating-point accelerator chips,
matrices. For all hypercubes built without floating-point accelerator chips, 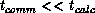 and, hence,
QCD simulations are extremely ``efficient,'' where efficiency
and, hence,
QCD simulations are extremely ``efficient,'' where efficiency  (Equations
(Equations 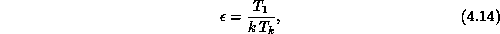
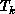 is the time taken for k processors to perform the given
calculation. Typically, such calculations have efficiencies in the range
is the time taken for k processors to perform the given
calculation. Typically, such calculations have efficiencies in the range
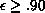 , which means they are ideally suited to this type of
computation since doubling the number of processors nearly halves the
total computational time required for solution. However, as we shall see
(for the Mark IIIfp hypercube, for example), the picture changes dramatically
when fast floating-point chips are used; then
, which means they are ideally suited to this type of
computation since doubling the number of processors nearly halves the
total computational time required for solution. However, as we shall see
(for the Mark IIIfp hypercube, for example), the picture changes dramatically
when fast floating-point chips are used; then 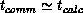 and
one must take some care in coding to obtain maximum performance.
and
one must take some care in coding to obtain maximum performance.
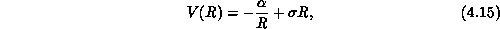
 is the coefficient of the
Coulombic potential and
is the coefficient of the
Coulombic potential and  is the string tension. In fitting
experimental charmonium data to this Coulomb plus linear potential, Eichten
et al. [
is the string tension. In fitting
experimental charmonium data to this Coulomb plus linear potential, Eichten
et al. [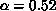 and
and
 =0.18GeV
=0.18GeV . Thus, a goal of the lattice calculations is to
reproduce these numbers. Enroute to this goal, it is necessary to show that
the numbers from the lattice are ``scaling,'' that is, if one calculates a
physical observable on lattices with different spacings then one gets the
same answer. This means that the artifacts due to the finiteness of the
lattice spacing have disappeared and continuum physics can be extracted.
. Thus, a goal of the lattice calculations is to
reproduce these numbers. Enroute to this goal, it is necessary to show that
the numbers from the lattice are ``scaling,'' that is, if one calculates a
physical observable on lattices with different spacings then one gets the
same answer. This means that the artifacts due to the finiteness of the
lattice spacing have disappeared and continuum physics can be extracted.
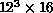 lattice with
lattice with
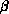 ranging from
ranging from 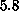 to
to 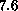 [
[ was found to be
was found to be 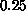 and the string tension (converting to
the dimensionless ratio)
and the string tension (converting to
the dimensionless ratio) 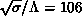 . The numbers
are quite a bit off from the charmonium data but the string tension did
appear to be scaling, albeit in the narrow window
. The numbers
are quite a bit off from the charmonium data but the string tension did
appear to be scaling, albeit in the narrow window 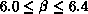 .
.
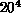 lattice with
lattice with 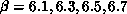 [
[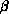 value,
value, 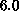 , and
investigated different lattice sizes:
, and
investigated different lattice sizes: 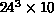 ,
, 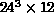 ,
, 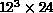 ,
, 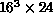 [
[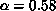 and
and
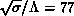 , that is,
, that is,  = 0.15GeV
= 0.15GeV ,
compare favorably with the charmonium data. This work is based on
about 1300 CPU hours on the 32-node Mark IIIfp hypercube, which has a
performance of roughly twice a CRAY X-MP
,
compare favorably with the charmonium data. This work is based on
about 1300 CPU hours on the 32-node Mark IIIfp hypercube, which has a
performance of roughly twice a CRAY X-MP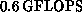 . As each node
runs at
. As each node
runs at 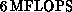 , this corresponds to a speedup of 100, and
hence, an efficiency of 78 percent. These figures are for the most
highly optimized code. The original version of the code written in C
ran on the Motorola chips at
, this corresponds to a speedup of 100, and
hence, an efficiency of 78 percent. These figures are for the most
highly optimized code. The original version of the code written in C
ran on the Motorola chips at 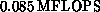 and on the Weitek
chips at
and on the Weitek
chips at 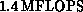 . The communication time, which is roughly
the same for both, is less than a 2 percent overhead for the former but
nearly 30 percent for the latter. When the computationally intensive
parts of the calculation are written in assembly code for the Weitek,
this overhead becomes almost 50 percent. This
. The communication time, which is roughly
the same for both, is less than a 2 percent overhead for the former but
nearly 30 percent for the latter. When the computationally intensive
parts of the calculation are written in assembly code for the Weitek,
this overhead becomes almost 50 percent. This  of
communication, shown in lines two and three in Table
of
communication, shown in lines two and three in Table 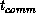 , is given by
, is given by
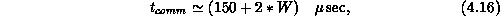
 by a factor of
by a factor of
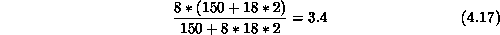
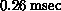 . On all hypercubes with fast floating-point
chips-and on most hypercubes without these chips for less
computationally intensive codes-such ``vectorization'' of
communication is often important. In Figure
. On all hypercubes with fast floating-point
chips-and on most hypercubes without these chips for less
computationally intensive codes-such ``vectorization'' of
communication is often important. In Figure 
