




Next: Stopping Criteria and Accuracy
Up: Symmetric Indefinite Lanczos Method
Previous: Some Properties of Symmetric
Contents
Index
Algorithm
In order to use a Lanczos procedure to solve the generalized
eigenproblem (8.21), we first convert it to an
equivalent standard eigenvalue
problem. Several transformations are possible; the most common ones are
listed below.
- (a)
- If one wants a few of the eigenvalues of
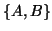 which are largest
in magnitude, and if the matrix
which are largest
in magnitude, and if the matrix  is nonsingular,
we may multiply by
is nonsingular,
we may multiply by 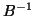 to obtain
to obtain
The matrix 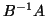 is symmetric with respect to
is symmetric with respect to  or
or  .
.
- (b)
- If one wants a few of the eigenvalues closest to a given value
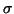 , we apply the SI
to obtain
, we apply the SI
to obtain
In particular, if the smallest eigenvalues in magnitude are
desired, one could choose the shift value 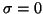 .
Note that the matrix
.
Note that the matrix
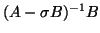 is symmetric with respect to
is symmetric with respect to  or
or 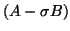 .
.
We will focus on case (b) in the rest of this section
and write the transformed problem as
where
Note that the eigenvalues of 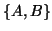 may be complex even when
may be complex even when  and
and  are real, so it may be necessary to use a value of
are real, so it may be necessary to use a value of 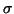 which is complex.
The Lanczos recursion may still be implemented using real arithmetic
even if a complex shift is used; see [362].
which is complex.
The Lanczos recursion may still be implemented using real arithmetic
even if a complex shift is used; see [362].
A symmetric indefinite Lanczos algorithm template is presented in
Algorithm 8.4.
The generated Lanczos vectors 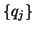 and scalars
and scalars
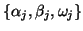 satisfy the
following governing equations:
satisfy the
following governing equations:
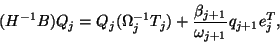 |
(235) |
where
The Lanczos vectors
![$Q_j = \left[ \begin{array}{cccc}
q_1 & q_2 & \cdots & q_j \\
\end{array} \right]$](img2908.png) are
are  orthogonal, i.e.,
orthogonal, i.e.,
and are normalized to have unit Euclidean norm,
i.e., 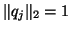 .
.
The reduced eigenvalue problem is
It inherits the same numerical difficulties as the original
problem. For example, Ritz value
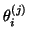 could be complex,
and even defective. In other words, it may belong
to a nondiagonal Jordan block of
could be complex,
and even defective. In other words, it may belong
to a nondiagonal Jordan block of
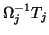 .
.
Once
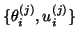 are computed, the right
and left Ritz vectors are defined as
are computed, the right
and left Ritz vectors are defined as
respectively.
The quantities
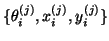 are referred to as Ritz triplets of the matrix
are referred to as Ritz triplets of the matrix 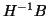 .
.
The (right) residual vectors 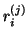 corresponding to the Ritz pairs
corresponding to the Ritz pairs
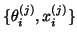 are
are
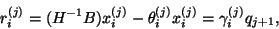 |
(236) |
where
Note that the last equality in (8.23)
is obtained by multiplying equation (8.22)
on the right by 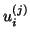 and the definition of
and the definition of 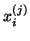 .
Note that the left residual vectors
.
Note that the left residual vectors
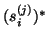 are related to
the right residual vectors
are related to
the right residual vectors 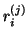 by
by
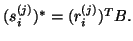 It follows that
It follows that
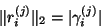 |
(237) |
and
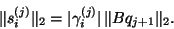 |
(238) |
Note that the vector 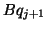 is directly available in every iteration of
the symmetric indefinite Lanczos algorithm.
No extra call on
is directly available in every iteration of
the symmetric indefinite Lanczos algorithm.
No extra call on  is necessary.
Therefore, one of the attractive features of the Lanczos algorithm
is that the residual vectors can be calculated without
explicitly computing Ritz vectors
is necessary.
Therefore, one of the attractive features of the Lanczos algorithm
is that the residual vectors can be calculated without
explicitly computing Ritz vectors 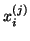 and
and 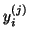 .
.

We now comment on some steps of Algorithm 8.4:
- (1)
- The ideal initial vector is one which is a linear combination of the
eigenvectors corresponding to the desired eigenvalues. If an approximation of
such a vector is
not available, then a random vector may be used. The initial vector
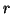 is often preprocessed by multiplying it by
is often preprocessed by multiplying it by 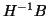 . This preprocessing step
was suggested in [161] and is essential when
. This preprocessing step
was suggested in [161] and is essential when  is singular; see
§8.6.4 for details.
is singular; see
§8.6.4 for details.
- (4) and (15)
- The matrix-vector multiplication
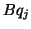 should be
performed by a user-provided subroutine which can take advantage of the
data structure of the matrix
should be
performed by a user-provided subroutine which can take advantage of the
data structure of the matrix  .
.
- (7)
- The linear system of equations
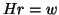 must be solved for
must be solved for 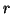 .
Let
.
Let
be the sparse LDL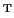 factorization (see §10.3)
computed before the for-loop. Then the vector
factorization (see §10.3)
computed before the for-loop. Then the vector 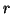 can be efficiently
computed in three steps:
can be efficiently
computed in three steps:
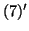 solve
solve 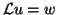 for
for 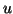
solve 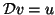 for
for 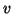
solve 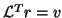 for
for 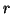
- (12)
- When
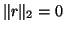 , it
indicates that all of the eigenvalues of the
, it
indicates that all of the eigenvalues of the 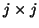 pencil
pencil
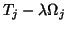 are also the eigenvalues of
are also the eigenvalues of 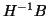 , and the columns of
, and the columns of
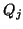 span an invariant subspace. One can either exit the algorithm or
continue the algorithm by setting
the value of
span an invariant subspace. One can either exit the algorithm or
continue the algorithm by setting
the value of 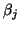 to zero and selecting
to zero and selecting 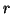 to be a random vector
which is
to be a random vector
which is  orthogonal to the columns of
orthogonal to the columns of 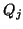 .
.
- (13)
- In finite precision arithmetic, the vectors
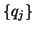 are no longer
are no longer  orthogonal. The schemes for reorthogonalization
which are discussed for the standard symmetric Lanczos procedure may be
extended to the symmetric indefinite algorithm; see §4.4
for details.
orthogonal. The schemes for reorthogonalization
which are discussed for the standard symmetric Lanczos procedure may be
extended to the symmetric indefinite algorithm; see §4.4
for details.
- (14)
- In the symmetric Lanczos algorithm (see §4.4),
the Lanczos vectors are scaled to be
 orthonormal,
orthonormal, 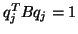 .
However, in the symmetric indefinite algorithm, the vectors are scaled so that
.
However, in the symmetric indefinite algorithm, the vectors are scaled so that
There are two reasons for the change in scaling, both of which have to do
with the indefiniteness of  . The first reason is that even when
. The first reason is that even when  and
and
 are real, scaling the Lanczos vectors so that
are real, scaling the Lanczos vectors so that 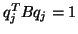 may involve
complex arithmetic.
(By keeping track of the sign of
may involve
complex arithmetic.
(By keeping track of the sign of 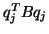 it is possible to avoid
complex arithmetic but still use
it is possible to avoid
complex arithmetic but still use
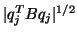 as a norm.
However, this algorithm is less stable.)
The second reason is that when
as a norm.
However, this algorithm is less stable.)
The second reason is that when  is indefinite, not
every subspace has a
is indefinite, not
every subspace has a  -orthonormal basis, and even if it does, it may be
highly ill-conditioned [417,20].
The choice of scaling does not remedy the possibility of
an ill-conditioned basis of Lanczos vectors.
However, it does provide a convenient means of detecting when the
basis is becoming ill-conditioned, specifically, a tiny value of
-orthonormal basis, and even if it does, it may be
highly ill-conditioned [417,20].
The choice of scaling does not remedy the possibility of
an ill-conditioned basis of Lanczos vectors.
However, it does provide a convenient means of detecting when the
basis is becoming ill-conditioned, specifically, a tiny value of
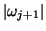 [357].
[357].
- (17)
- If
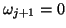 , the Lanczos procedure suffers a
breakdown similar to the breakdown which occurs in the non-Hermitian
Lanczos procedure; see §7.8.
The same remedies developed for the
non-Hermitian Lanczos procedure, such as look-ahead
[364,178] and adaptive blocking [29,298], can be
employed.
, the Lanczos procedure suffers a
breakdown similar to the breakdown which occurs in the non-Hermitian
Lanczos procedure; see §7.8.
The same remedies developed for the
non-Hermitian Lanczos procedure, such as look-ahead
[364,178] and adaptive blocking [29,298], can be
employed.
- (19)
- The approximate eigenvalues of the matrix pencil
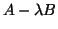 are determined
by solving the reduced
are determined
by solving the reduced 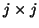 generalized eigenvalue problem
generalized eigenvalue problem
There are several algorithms available for solving this problem.
If  is small, one could apply the standard QZ algorithm to
is small, one could apply the standard QZ algorithm to
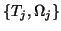 or the QR algorithm to
or the QR algorithm to
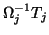 .
However, neither of these algorithms take advantage of the structure of
.
However, neither of these algorithms take advantage of the structure of
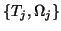 . A good survey of algorithms which exploit the symmetry of
. A good survey of algorithms which exploit the symmetry of
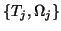 is contained in [357],
and some more recent work can be found in [406,407].
is contained in [357],
and some more recent work can be found in [406,407].
For even moderate values of
 (e.g.,
(e.g., 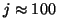 ), solving the reduced problem becomes computationally
significant. For long Lanczos runs, it is recommended to solve the reduced
problem periodically, perhaps once in every five or ten Lanczos iterations.
), solving the reduced problem becomes computationally
significant. For long Lanczos runs, it is recommended to solve the reduced
problem periodically, perhaps once in every five or ten Lanczos iterations.
A proper stopping criterion for the inner loop of the
symmetric indefinite Lanczos method is
where 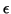 is a user-given tolerance value.
Note that
is a user-given tolerance value.
Note that 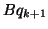 is available at the end of a Lanczos run,
and its Euclidean norm can be computed at the cost of one dot product.
No extra call on
is available at the end of a Lanczos run,
and its Euclidean norm can be computed at the cost of one dot product.
No extra call on  is necessary for that term.
An elaborate testing procedure for the convergence is discussed
in the following §8.6.3.
is necessary for that term.
An elaborate testing procedure for the convergence is discussed
in the following §8.6.3.
- (21)
- Compute the approximate eigenvectors only when the
corresponding Ritz values have converged according to the test described below.





Next: Stopping Criteria and Accuracy
Up: Symmetric Indefinite Lanczos Method
Previous: Some Properties of Symmetric
Contents
Index
Susan Blackford
2000-11-20
![]() and scalars
and scalars
![]() satisfy the
following governing equations:
satisfy the
following governing equations:
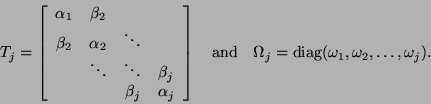
![]() are
are ![]() orthogonal, i.e.,
orthogonal, i.e.,
![]() are computed, the right
and left Ritz vectors are defined as
are computed, the right
and left Ritz vectors are defined as
![]() corresponding to the Ritz pairs
corresponding to the Ritz pairs
![]() are
are
solve
for
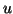
for
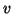
for
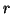
![]() (e.g.,
(e.g., ![]() ), solving the reduced problem becomes computationally
significant. For long Lanczos runs, it is recommended to solve the reduced
problem periodically, perhaps once in every five or ten Lanczos iterations.
), solving the reduced problem becomes computationally
significant. For long Lanczos runs, it is recommended to solve the reduced
problem periodically, perhaps once in every five or ten Lanczos iterations.