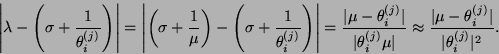Next: Singular
Up: Symmetric Indefinite Lanczos Method
Previous: Algorithm
Contents
Index
Stopping Criteria and Accuracy Assessment
Since the eigenproblem of a symmetric indefinite pencil
does not have any special
mathematical properties, we may refer to techniques developed for general
non-Hermitian matrices to assess the quality of the approximate eigentriplets
of an indefinite pencil. Nonetheless, we can take advantage of the symmetry
to simplify the analysis and subsequently the error bound. The simplification
stems from the simple relation between the right and left eigenvectors of
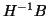 . If
. If 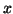 is a right eigenvector of
is a right eigenvector of 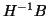 ,
then
,
then 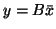 is the corresponding left eigenvector.
is the corresponding left eigenvector.
To assess the accuracy of a Ritz triplet
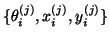 ,
by the discussion in §7.8,
it is known that there is a matrix
,
by the discussion in §7.8,
it is known that there is a matrix 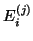 such that
such that
where
In fact,
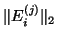 is the optimal backward error.
By the standard first-order perturbation expansion or the error
bound presented in §7.13, there is an
eigenvalue
is the optimal backward error.
By the standard first-order perturbation expansion or the error
bound presented in §7.13, there is an
eigenvalue 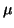 of
of 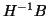 , such that
, such that
where we have made use of equations (8.24), (8.25), and the
equality
Furthermore, to avoid a bound which explicitly involves the Ritz
vectors 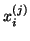 , we note that
, we note that
and
where it is assumed that
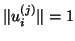 .
Recall that the columns of
.
Recall that the columns of 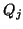 are normalized to 1.
The value of
are normalized to 1.
The value of
may be updated in each Lanczos iteration.
Therefore the error
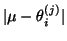 can also
be bounded by
can also
be bounded by
which does not explicitly use the Ritz vector 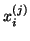 .
In conclusion, one may use
.
In conclusion, one may use
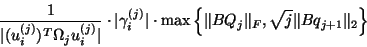 |
(239) |
as a provisional error estimate in the inner loop of
Algorithm 8.4 (i.e., step (19)).
Only when the required number of Ritz
values
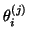 have passed this test, and not before,
may the Ritz vectors
have passed this test, and not before,
may the Ritz vectors 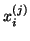 be computed. At that point the more
precise factor,
be computed. At that point the more
precise factor,
may be computed at the extra cost of forming 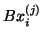 .
.
The Ritz values
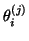 approximate the eigenvalues of
approximate the eigenvalues of 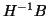 ,
while the quantities
,
while the quantities
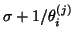 are approximations to the eigenvalues
are approximations to the eigenvalues
 of the original problem (8.21). We can estimate
of the original problem (8.21). We can estimate
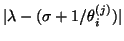 using the bound above and
using the bound above and





Next: Singular
Up: Symmetric Indefinite Lanczos Method
Previous: Algorithm
Contents
Index
Susan Blackford
2000-11-20
![]() . If
. If ![]() is a right eigenvector of
is a right eigenvector of ![]() ,
then
,
then ![]() is the corresponding left eigenvector.
is the corresponding left eigenvector.
![]() ,
by the discussion in §7.8,
it is known that there is a matrix
,
by the discussion in §7.8,
it is known that there is a matrix ![]() such that
such that
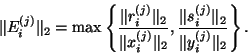
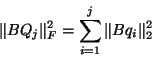
![]() approximate the eigenvalues of
approximate the eigenvalues of ![]() ,
while the quantities
,
while the quantities
![]() are approximations to the eigenvalues
are approximations to the eigenvalues
![]() of the original problem (8.21). We can estimate
of the original problem (8.21). We can estimate
![]() using the bound above and
using the bound above and