




Next: Lanczos Algorithm with SI.
Up: Lanczos Methods A.
Previous: Lanczos Methods A.
Contents
Index
In the direct iteration variant,
we multiply with  and solve systems with
and solve systems with  ;
this corresponds to
;
this corresponds to 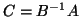 . It computes a
basis
. It computes a
basis 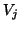 , where the matrix pencil
, where the matrix pencil  is represented by a
real symmetric tridiagonal matrix,
is represented by a
real symmetric tridiagonal matrix,
![\begin{displaymath}
T_{j}=\left[
\begin{array}{cccc}\alpha_1 & \beta_1 &&\\
\be...
...beta_{j-1}\\
&&\beta_{j-1}&\alpha_j\\
\end{array} \right]\;,
\end{displaymath}](img859.png) |
(72) |
satisfying the basic recursion,
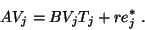 |
(73) |
Compare this to the standard Hermitian case (4.10).
Now the basis 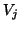 is
is  -orthogonal,
-orthogonal,
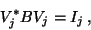 |
(74) |
and the matrix 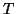 is congruent to a section of
is congruent to a section of  ,
,
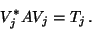 |
(75) |
We simplify the description of the  -orthogonalization
by introducing an auxiliary basis,
-orthogonalization
by introducing an auxiliary basis,
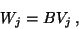 |
(76) |
which is 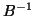 -orthogonal,
-orthogonal,
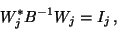 |
(77) |
and for which 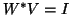 .
.
Precisely as in the standard case,
compute an eigensolution of 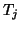 ,
,
and get a
Ritz value
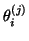 and a Ritz vector,
and a Ritz vector,
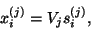 |
(78) |
approximating an eigenpair of the pencil (5.1).
Its residual,
is  -orthogonal to the Krylov space spanned by
-orthogonal to the Krylov space spanned by 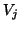 .
.
We may estimate the norm of the residual as we did in
the standard Hermitian case, (4.13), but now
this is better done using the 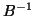 -norm getting
-norm getting
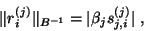 |
(79) |
using the fact that
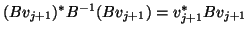 .
It is natural to use the
.
It is natural to use the 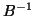 -norm when measuring convergence;
see [353, Chap. 15].
-norm when measuring convergence;
see [353, Chap. 15].
As in the standard case we need to
monitor the subdiagonal elements 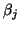 of
of 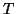 ,
and the last elements
,
and the last elements 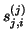 of its eigenvectors. As soon as this
product is small, we may flag an eigenvalue as converged,
without actually performing the matrix-vector
multiplication (5.14). We save this
operation until the step
of its eigenvectors. As soon as this
product is small, we may flag an eigenvalue as converged,
without actually performing the matrix-vector
multiplication (5.14). We save this
operation until the step  when the estimate (5.15)
indicates convergence.
when the estimate (5.15)
indicates convergence.
We get the following algorithm.

Let us comment on this algorithm step by step:
- (1)
- If a good guess for the wanted eigenvector is available, use it as the
starting
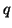 . In other cases choose a random direction, for instance,
one consisting of normally distributed random numbers. Notice that
. In other cases choose a random direction, for instance,
one consisting of normally distributed random numbers. Notice that
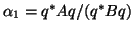 is the Rayleigh quotient of the
starting vector and that
is the Rayleigh quotient of the
starting vector and that 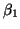 measures the
measures the 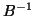 -norm of its
residual (5.15).
-norm of its
residual (5.15).
- (4)
- This is where the large matrix
 comes in.
Any routine
that performs a matrix-vector multiplication can be used.
comes in.
Any routine
that performs a matrix-vector multiplication can be used.
- (8)
- It is sufficient to reorthogonalize just one of the bases
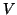 or
or 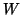 ,
not both of them.
The choices are the same as in the standard case:
,
not both of them.
The choices are the same as in the standard case:
- Full:
Now we want to make the
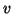 basis vectors
basis vectors  -orthogonal,
computing
-orthogonal,
computing
and repeat until the vector 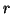 is orthogonal to the basis
is orthogonal to the basis 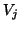 .
We have to apply one matrix-vector multiplication by
.
We have to apply one matrix-vector multiplication by  for each reorthogonalization, and we have to use the classical
variant of the Gram-Schmidt process.
for each reorthogonalization, and we have to use the classical
variant of the Gram-Schmidt process.
We may avoid these extra multiplications with  if we save both bases
if we save both bases 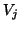 and
and 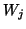 and subtract multiples of the
columns of
and subtract multiples of the
columns of 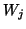 ,
,
until orthogonality is obtained, almost always just once.
Now we may use a modified Gram-Schmidt orthogonalization.
- Selective: Reorthogonalize only when necessary,
one has to monitor the orthogonality as described in
§4.4.4
for the standard case. Note that now the symmetric matrix
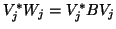 is involved and some of the vectors
is involved and some of the vectors 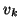 have to be replaced by the corresponding vectors
have to be replaced by the corresponding vectors 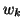 .
.
- Local: Used for huge matrices, when it is difficult to store
the whole basis
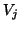 . Advisable only when one or two extreme eigenvalues
are sought. We make sure that
. Advisable only when one or two extreme eigenvalues
are sought. We make sure that 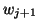 is orthogonal to
is orthogonal to 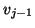 and
and
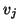 by subtracting
by subtracting
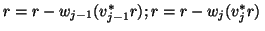 once
in this step.
once
in this step.
- (9)
- Here we need to solve a system with the positive
definite matrix
 . This was not needed in the standard case
(4.1).
. This was not needed in the standard case
(4.1).
- (11)
- For each step
 , or at appropriate intervals,
compute the eigenvalues
, or at appropriate intervals,
compute the eigenvalues
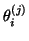 and eigenvectors
and eigenvectors 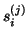 of the symmetric tridiagonal matrix
of the symmetric tridiagonal matrix
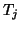 (5.8). Same procedure as for the standard case.
(5.8). Same procedure as for the standard case.
- (12)
- The algorithm is stopped when a sufficiently
large basis
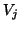 has been found, so that eigenvalues
has been found, so that eigenvalues
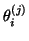 of
the tridiagonal matrix
of
the tridiagonal matrix 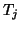 (5.8)
give good approximations to all
the eigenvalues of the pencil (5.1) sought.
(5.8)
give good approximations to all
the eigenvalues of the pencil (5.1) sought.
The estimate (5.15) for the residual
may be too optimistic if the basis
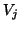 is not fully
is not fully  -orthogonal.
Then the Ritz vector
-orthogonal.
Then the Ritz vector 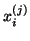 (5.14) may have its norm
smaller than
(5.14) may have its norm
smaller than 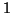 , and we have to replace the estimate by,
, and we have to replace the estimate by,
- (14)
- The eigenvectors of the original matrix pencil (5.1) are computed only
when the test in step (5.4) has indicated that they
have converged. Then the basis
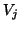 is used in a matrix-vector
multiplication to get the
eigenvector (5.14),
is used in a matrix-vector
multiplication to get the
eigenvector (5.14),
for each 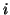 that is flagged as converged.
that is flagged as converged.





Next: Lanczos Algorithm with SI.
Up: Lanczos Methods A.
Previous: Lanczos Methods A.
Contents
Index
Susan Blackford
2000-11-20
![\begin{displaymath}
T_{j}=\left[
\begin{array}{cccc}\alpha_1 & \beta_1 &&\\
\be...
...beta_{j-1}\\
&&\beta_{j-1}&\alpha_j\\
\end{array} \right]\;,
\end{displaymath}](img859.png)
![]() -orthogonalization
by introducing an auxiliary basis,
-orthogonalization
by introducing an auxiliary basis,
![]() ,
,
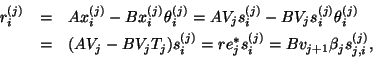
![]() -norm getting
-norm getting
![]() of
of ![]() ,
and the last elements
,
and the last elements ![]() of its eigenvectors. As soon as this
product is small, we may flag an eigenvalue as converged,
without actually performing the matrix-vector
multiplication (5.14). We save this
operation until the step
of its eigenvectors. As soon as this
product is small, we may flag an eigenvalue as converged,
without actually performing the matrix-vector
multiplication (5.14). We save this
operation until the step ![]() when the estimate (5.15)
indicates convergence.
when the estimate (5.15)
indicates convergence.
![]() if we save both bases
if we save both bases ![]() and
and ![]() and subtract multiples of the
columns of
and subtract multiples of the
columns of ![]() ,
,
![]() is not fully
is not fully ![]() -orthogonal.
Then the Ritz vector
-orthogonal.
Then the Ritz vector ![]() (5.14) may have its norm
smaller than
(5.14) may have its norm
smaller than ![]() , and we have to replace the estimate by,
, and we have to replace the estimate by,