Spectral Transformation Techniques



Next: Tradeoffs
Up: Parallel Spectral Divide
Previous: The SDC algorithm
Although Algorithms 1 and 2 only divide the spectrum along the pure imaginary
axis and the unit circle, respectively,
we can use Möbius and other simple transformations of the
input matrix 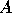 to divide along other more general curves.
As a result, we can compute the eigenvalues (and corresponding invariant
subspace)
inside any region defined as the intersection of regions defined by these
curves. This is a major attraction of this kind of algorithm.
to divide along other more general curves.
As a result, we can compute the eigenvalues (and corresponding invariant
subspace)
inside any region defined as the intersection of regions defined by these
curves. This is a major attraction of this kind of algorithm.
Let us show how to use Möbius transformations to divide the spectrum
along arbitrary lines and circles.
Transform the eigenproblem 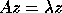 to
to
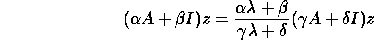
Then if we apply Algorithm 1 to
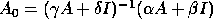 we can split the spectrum with respect to a region
we can split the spectrum with respect to a region

If we apply Algorithm 2 to 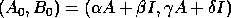 , we can split along the curve
, we can split along the curve

For example, by computing the matrix sign function of
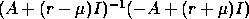 , then Algorithm 1
will split the spectrum of
, then Algorithm 1
will split the spectrum of 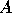 along a circle centered
at
along a circle centered
at 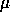 with radius
with radius  . If
. If 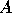 is real, and we choose
is real, and we choose 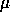 to be real,
then all arithmetic will be real.
to be real,
then all arithmetic will be real.
If 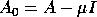 and
and 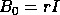 ,
then Algorithm 2 will split the spectrum of
,
then Algorithm 2 will split the spectrum of 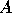 along
a circle centered at
along
a circle centered at 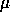 with radius
with radius  . If
. If 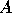 is real, and
we choose
is real, and
we choose 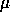 to be real, then all arithmetic in the
algorithm will be real.
to be real, then all arithmetic in the
algorithm will be real.
Other more general regions can be obtained by taking 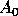 as a
polynomial function of
as a
polynomial function of 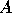 . For example, by computing the matrix
sign function of
. For example, by computing the matrix
sign function of 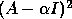 , we can divide the spectrum within
a ``bowtie'' shaped region centered at
, we can divide the spectrum within
a ``bowtie'' shaped region centered at 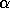 . Figure 1
illustrates the regions which the algorithms can deal with assuming
that
. Figure 1
illustrates the regions which the algorithms can deal with assuming
that 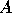 is real and the algorithms use only real arithmetic.
is real and the algorithms use only real arithmetic.

Figure 1: Different Geometric Regions for the Spectral Decomposition
Jack Dongarra
Mon Jan 9 11:07:50 EST 1995
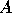 to divide along other more general curves.
As a result, we can compute the eigenvalues (and corresponding invariant
subspace)
inside any region defined as the intersection of regions defined by these
curves. This is a major attraction of this kind of algorithm.
to divide along other more general curves.
As a result, we can compute the eigenvalues (and corresponding invariant
subspace)
inside any region defined as the intersection of regions defined by these
curves. This is a major attraction of this kind of algorithm.
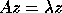 to
to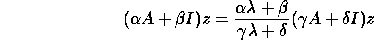
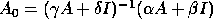 we can split the spectrum with respect to a region
we can split the spectrum with respect to a region 
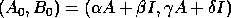 , we can split along the curve
, we can split along the curve 
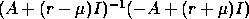 , then Algorithm 1
will split the spectrum of
, then Algorithm 1
will split the spectrum of 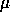 with radius
with radius  . If
. If 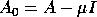 and
and 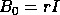 ,
then Algorithm 2 will split the spectrum of
,
then Algorithm 2 will split the spectrum of 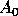 as a
polynomial function of
as a
polynomial function of 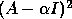 , we can divide the spectrum within
a ``bowtie'' shaped region centered at
, we can divide the spectrum within
a ``bowtie'' shaped region centered at 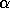 . Figure
. Figure 