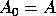 ,
, 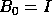 ;
;
The above algorithm needs an explicit matrix inverse. This could cause numerical instability when the matrix is ill-conditioned. The following algorithm, originally due to Godunov, Bulgakov and Malyshev [44][10][30] and modified by Bai, Demmel and Gu [7], eliminates the need for the matrix inverse, and divides the spectrum along the unit circle instead of the imaginary axis. We first describe the algorithm, and then briefly explain why it works.
ALGORITHM 2 (THE SDC ALGORITHM WITH INVERSE FREE ITERATION)
Let 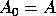 ,
, 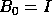 ;
;
For 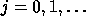 until convergence or
until convergence or 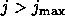 do
do
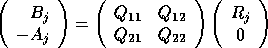 ; ~ (QR decomposition)
; ~ (QR decomposition)
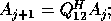
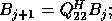
if 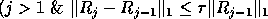 ),
), 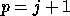 , exit
, exit
End for;
Compute 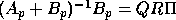 ;
~ (rank revealing QR decomposition)
;
~ (rank revealing QR decomposition)
Let 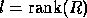 ;
;
Compute 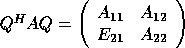 ;
;
Compute 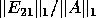 .
.
As in Algorithm 1, we need to choose
a stopping
criterion  in the inner loop, as well as a limit
in the inner loop, as well as a limit 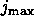 on the
maximum number of iterations.
On convergence, the eigenvalues of
on the
maximum number of iterations.
On convergence, the eigenvalues of 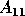 are the eigenvalues of
are the eigenvalues of 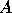 inside the unit disk
inside the unit disk 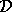 , and the eigenvalues of
, and the eigenvalues of 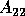 are the
eigenvalues of
are the
eigenvalues of 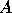 outside
outside 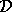 .
It is assumed that no eigenvalues of
.
It is assumed that no eigenvalues of 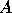 are on the unit circle.
As with Algorithm 1, the quantity
are on the unit circle.
As with Algorithm 1, the quantity
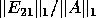 measures the backward stability.
measures the backward stability.
To illustrate how the algorithm works we will assume that all matrices we want to invert are invertible. From the inner loop of the algorithm, we see that
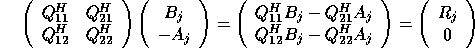
so 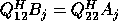 or
or 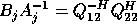 .
Therefore
.
Therefore
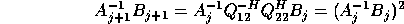
so the algorithm is simply repeatedly squaring the eigenvalues, driving the
ones inside the unit circle to 0 and those outside to 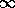 . Repeated
squaring yields quadratic convergence. This is analogous to the sign function
iteration where computing
. Repeated
squaring yields quadratic convergence. This is analogous to the sign function
iteration where computing 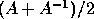 is equivalent to taking the Cayley
transform
is equivalent to taking the Cayley
transform 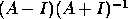 of
of 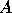 , squaring, and taking the inverse Cayley
transform.
Further explanation of how the algorithm works can be found in
[7].
, squaring, and taking the inverse Cayley
transform.
Further explanation of how the algorithm works can be found in
[7].
An attraction of this algorithm is that it can equally well deal with the
generalized nonsymmetric eigenproblem 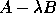 , provided the problem
is regular, i.e.
, provided the problem
is regular, i.e. 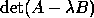 is not identically zero.
One simply has to start the algorithm with
is not identically zero.
One simply has to start the algorithm with 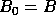 instead of
instead of 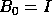 .
.
Regarding the QR decomposition in the inner loop,
there is no need to form the entire 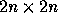 unitary matrix
unitary matrix 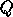 in order to get the submatrices
in order to get the submatrices 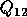 and
and 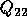 .
Instead, we can compute the QR decomposition of the
.
Instead, we can compute the QR decomposition of the
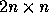 matrix
matrix 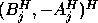 ,
which leaves
,
which leaves  stored implicitly as Householder vectors
in the lower triangular part of the matrix and another
stored implicitly as Householder vectors
in the lower triangular part of the matrix and another  dimensional array.
We can then apply
dimensional array.
We can then apply  - without computing it - to the
- without computing it - to the
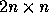 matrix
matrix 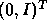 to obtain the desired
matrices
to obtain the desired
matrices 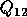 and
and 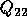 .
.
We now show how to compute 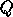 in the rank revealing QR decomposition
of
in the rank revealing QR decomposition
of 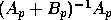 without computing
the explicit inverse
without computing
the explicit inverse 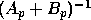 and subsequent products.
This will yield the ultimate inverse free algorithm.
Recall that for our purposes, we only need the unitary factor
and subsequent products.
This will yield the ultimate inverse free algorithm.
Recall that for our purposes, we only need the unitary factor 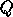 and the
rank of
and the
rank of 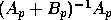 .
It turns out that by using the generalized QR decomposition technique
developed in [2][45],
we can get the desired information without computing
.
It turns out that by using the generalized QR decomposition technique
developed in [2][45],
we can get the desired information without computing
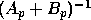 . In fact, in order to compute the QR decomposition with
pivoting of
. In fact, in order to compute the QR decomposition with
pivoting of 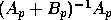 , we first compute the QR decomposition
with pivoting of the matrix
, we first compute the QR decomposition
with pivoting of the matrix 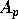 :
:
and then we compute the RQ factorization of the matrix 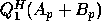 :
:
From (2.7) and (2.8), we have
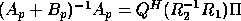 .
The
.
The 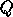 is the desired unitary factor. The rank of
is the desired unitary factor. The rank of 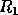 is also
the rank of the matrix
is also
the rank of the matrix 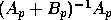 .
.