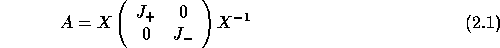
Both spectral divide and conquer (SDC) algorithms discussed in this paper can be presented in the following framework. Let
be the Jordan canonical form of 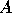 , where the eigenvalues of the
, where the eigenvalues of the  submatrix
submatrix 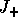 are the eigenvalues of
are the eigenvalues of 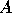 inside a
selected region
inside a
selected region 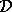 in the complex plane,
and the eigenvalues of the
in the complex plane,
and the eigenvalues of the
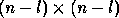 submatrix
submatrix 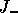 are the eigenvalues of
are the eigenvalues of 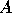 outside
outside 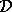 .
We assume that there are no eigenvalues of
.
We assume that there are no eigenvalues of 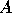 on the boundary
of
on the boundary
of 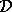 , otherwise we reselect or move the region
, otherwise we reselect or move the region 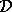 slightly.
The invariant subspace of the matrix
slightly.
The invariant subspace of the matrix 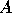 corresponding to the
eigenvalues inside
corresponding to the
eigenvalues inside 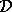 are spanned
by the first
are spanned
by the first 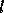 columns of
columns of 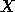 . The matrix
. The matrix
is the corresponding spectral projector.
Let 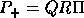 be the rank revealing QR decomposition of the
matrix
be the rank revealing QR decomposition of the
matrix 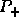 , where
, where 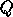 is unitary,
is unitary, 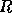 is upper triangular,
and
is upper triangular,
and 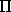 is a permutation matrix chosen
so that the leading
is a permutation matrix chosen
so that the leading 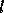 columns of
columns of 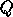 span the range space of
span the range space of 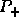 . Then
. Then 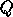 yields the desired spectral
decomposition:
yields the desired spectral
decomposition:
where the eigenvalues of 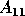 are the eigenvalues of
are the eigenvalues of 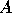 inside
inside
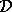 , and the eigenvalues of
, and the eigenvalues of 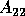 are the
eigenvalues of
are the
eigenvalues of 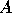 outside
outside 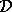 .
By substituting the complementary projector
.
By substituting the complementary projector 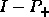 for
for 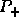 in (2.4),
in (2.4),
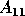 will have the eigenvalues outside
will have the eigenvalues outside 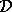 and
and
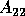 will have the eigenvalues inside
will have the eigenvalues inside 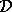 .
.
The crux of a parallel SDC algorithm is to efficiently
compute the desired spectral projector 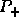 without
computing the Jordan canonical form.
without
computing the Jordan canonical form.