




Next: 12.5.5 Results
Up: Fast Vortex Algorithm
Previous: 12.5.3 Hypercube Implementation
Since our objective is to compute the flow around a cylinder, the efficiency
of the parallel implementation was tested on such a problem. The region for
which 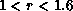 is uniformly covered with N particles. The parallel
efficiency is shown on Figure 12.19 as a function of the
hypercube size. The parallel implementation is fairly robust: The parallel
efficiency,
is uniformly covered with N particles. The parallel
efficiency is shown on Figure 12.19 as a function of the
hypercube size. The parallel implementation is fairly robust: The parallel
efficiency,  , remains larger than
, remains larger than 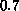 . The number of vortices per
processor was kept roughly constant at 1500 even if the parallel efficiency
is not a strong function of the size of the problem. It is, however, much
more sensitive to the quality of the domain decomposition. The fast parallel
algorithm performs better when all the subdomains have approximately the
same squarish shape or in other words, when the largest group assigned to a
processor is as compact as possible.
. The number of vortices per
processor was kept roughly constant at 1500 even if the parallel efficiency
is not a strong function of the size of the problem. It is, however, much
more sensitive to the quality of the domain decomposition. The fast parallel
algorithm performs better when all the subdomains have approximately the
same squarish shape or in other words, when the largest group assigned to a
processor is as compact as possible.
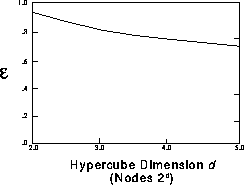
Figure 12.19: Parallel Efficiency of the Fast Algorithm
The results of Figure 12.19 were obtained at early times when the
Lagrangian particles are still distributed evenly around the cylinder which
makes the domain decomposition an easier task. At later times, the
distribution of the vortices does not allow the decomposition of the domain
in groups having approximately the same radius and the same number of
vortices. Some subdomains cover a larger region of space and as a result,
the efficiency drops to approximately 0.6. This is mainly due to the fact
that more processors end up in the near field of a processor responsible for
a large group; the request lists are longer and more data has to be moved
between processors.
The sources of overhead corresponding to Figure 12.19 are shown
on Figure 12.20 normalized with the useful work. Load imbalance,
the largest overhead contributor, is defined as the difference between the
maximum useful work reported by a processor and the average useful work per
processor. Further, the extra work includes the time spent making a copy of
one's own data structure, the time required to absorb the returning
information, and the work that was duplicated in all processors, namely, the
search for acceptable interactions in the upper portion of the tree and the
subsequent creation of the request lists. The remaining overhead has been
lumped under communication time although most of it is probably idle time (or
synchronization time) that was not included in the definition of load
imbalance.
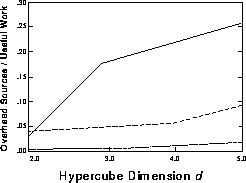
Figure 12.20: Load Imbalance (solid), Communication and Synchronization Time
(dash), and Extra Work (dot-dash) as a Function of the Number of
Processors
We expected that as P increases, the near field of a processor would
eventually contain a fixed number of neighboring processors. The number of
messages and the load imbalance would then reach an asymptote and the loss of
efficiency would be driven by the much smaller communication and extra times.
However, this has yet to happen at 32 processors and the communication time
is already starting to make an impact.
Nevertheless, the fast algorithm, its reasonably efficient parallel
implementation and the speed of the Mark III have made possible simulations
with as many as 80,000 vortex particles.





Next: 12.5.5 Results
Up: Fast Vortex Algorithm
Previous: 12.5.3 Hypercube Implementation
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
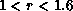 is uniformly covered with N particles. The parallel
efficiency is shown on Figure 12.19 as a function of the
hypercube size. The parallel implementation is fairly robust: The parallel
efficiency,
is uniformly covered with N particles. The parallel
efficiency is shown on Figure 12.19 as a function of the
hypercube size. The parallel implementation is fairly robust: The parallel
efficiency,  , remains larger than
, remains larger than 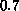 . The number of vortices per
processor was kept roughly constant at 1500 even if the parallel efficiency
is not a strong function of the size of the problem. It is, however, much
more sensitive to the quality of the domain decomposition. The fast parallel
algorithm performs better when all the subdomains have approximately the
same squarish shape or in other words, when the largest group assigned to a
processor is as compact as possible.
. The number of vortices per
processor was kept roughly constant at 1500 even if the parallel efficiency
is not a strong function of the size of the problem. It is, however, much
more sensitive to the quality of the domain decomposition. The fast parallel
algorithm performs better when all the subdomains have approximately the
same squarish shape or in other words, when the largest group assigned to a
processor is as compact as possible.






