




Next: 12.5.1 Vortex Methods
Up: Irregular Loosely Synchronous
Previous: 12.4.5 Comments on Performance
Vortex methods are a powerful tool for the
simulation of incompressible flows at high
Reynolds number. They rely on a discrete Lagrangian representation of
the vorticity field to approximately satisfy the Kelvin and Helmholtz
theorems which govern the dynamics of vorticity for inviscid flows. A
time-splitting technique can be used to include viscous effects. The
diffusion equation is considered separately after convecting the
particles with an inviscid vortex method. In our work, the viscous
effects are represented by the so-called deterministic method. The
approach was extended to problems where a flux of vorticity is used to
enforce the no-slip boundary condition.
In order to accurately compute the viscous transport of vorticity, gradients
need to be well resolved. As the Reynolds number is increased, these
gradients get steeper and more particles are required to achieve the
requisite resolution. In practice, the computing cost associated with the
convection step dictates the number of vortex particles and puts an upper
bound on the Reynolds number that can be simulated with confidence. That
threshold can be increased by reducing the asymptotic time complexity of the
convection step from 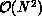 to
to 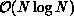 . The nearfield
of every vortex particle is identified. Within that region, the velocity is
computed by considering the pairwise interaction of vortices. The speedup
is achieved by approximating the influence of the rest of the domain, the
farfield. In that context, the interaction of two vortex particles is
treated differently depending on their spatial relation. The resulting
computer code does not lend itself to vectorization but has been successfully
implemented on concurrent computers.
. The nearfield
of every vortex particle is identified. Within that region, the velocity is
computed by considering the pairwise interaction of vortices. The speedup
is achieved by approximating the influence of the rest of the domain, the
farfield. In that context, the interaction of two vortex particles is
treated differently depending on their spatial relation. The resulting
computer code does not lend itself to vectorization but has been successfully
implemented on concurrent computers.
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
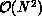 to
to 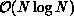 . The nearfield
of every vortex particle is identified. Within that region, the velocity is
computed by considering the pairwise interaction of vortices. The speedup
is achieved by approximating the influence of the rest of the domain, the
farfield. In that context, the interaction of two vortex particles is
treated differently depending on their spatial relation. The resulting
computer code does not lend itself to vectorization but has been successfully
implemented on concurrent computers.
. The nearfield
of every vortex particle is identified. Within that region, the velocity is
computed by considering the pairwise interaction of vortices. The speedup
is achieved by approximating the influence of the rest of the domain, the
farfield. In that context, the interaction of two vortex particles is
treated differently depending on their spatial relation. The resulting
computer code does not lend itself to vectorization but has been successfully
implemented on concurrent computers.




