




Next: 12.5.4 Efficiency of Parallel
Up: Fast Vortex Algorithm
Previous: 12.5.2 Fast Algorithms
The global nature of the 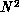 approach has made its parallel
implementation fairly straightforward (see [Fox:88a]). However,
as we have already seen in Section 12.4, that character was
drastically changed by the fast algorithm as it introduced a strong
component of locality. Globality is still present since the influence
of particle is felt throughout the domain, but more care and
computational effort is given to its near field. The fast parallel
algorithm has to reflect that dual nature, otherwise an efficient
implementation will never be obtained. Moreover, the domain
decomposition can no longer ignore the spatial distribution of the
vortices. Nearby vortices are strongly coupled computationally, so it
makes sense to assign them to the same processor. Binary bisection is
used in the host to spatially decompose the domain. Then, only the
vortices are sent to the processors where a binary tree is locally
built on top of them. For example, Figure 12.17 shows the
portion of the data structure assigned to processor 1 in a
4-processor environment.
approach has made its parallel
implementation fairly straightforward (see [Fox:88a]). However,
as we have already seen in Section 12.4, that character was
drastically changed by the fast algorithm as it introduced a strong
component of locality. Globality is still present since the influence
of particle is felt throughout the domain, but more care and
computational effort is given to its near field. The fast parallel
algorithm has to reflect that dual nature, otherwise an efficient
implementation will never be obtained. Moreover, the domain
decomposition can no longer ignore the spatial distribution of the
vortices. Nearby vortices are strongly coupled computationally, so it
makes sense to assign them to the same processor. Binary bisection is
used in the host to spatially decompose the domain. Then, only the
vortices are sent to the processors where a binary tree is locally
built on top of them. For example, Figure 12.17 shows the
portion of the data structure assigned to processor 1 in a
4-processor environment.
In a fast algorithm context, sending a copy of local data structure to
half the other processors does not necessarily result in a load
balanced implementation. The work associated with
processor-to-processor interactions now depends on their respective
location in physical space. A processor whose vortices are located at
the center of the domain is involved in more costly interactions than a
peripheral processor. To achieve the best possible load balancing,
that central processor could send a copy of its data to more than half
of the other processors and hence itself be responsible for a smaller
fraction of the work associated with its vortices.
Before a decision is made on which one is going to visit and which
to receive, we minimize the number of pairs of processors that
need to exchange their data structure. Following the domain
decomposition, the portion of the data structure that sits above the
subtrees is not present anywhere in the hypercube. That gap is filled
by broadcasting the description of the largest group of every
processor. By limiting the broadcast to one group per
processor, a small amount of data is actually exchanged but, as seen on
Figure 12.18, this step gives every processor a coarse
description of its surroundings and helps it find its place in the
universe.

Figure 12.17: Data Structure Assigned to Processor 1

Figure 12.18: Data Structure Known to Processor 1 After Broadcast
If the vortices of processor A are far enough from those of processor
B, it is even possible to use that coarse description to compute the
interaction of A and B without an additional exchange of
information. The far field of every processor can be quickly disposed of.
After thinking globally, one now has to act locally; if the vortices of
A are adjacent to those of B, a more detailed description of
their vorticity field is needed to compute their mutual influence.
This requires a transfer of information from either A to B or
from B to A. In the latter case, most of the work involved in
the A-B interaction takes place in processor A. Obviously,
processor B should not always send its information away since it would
then remain idle while the rest of the hypercube is working. Load-balancing
concerns will dictate the flow of information.





Next: 12.5.4 Efficiency of Parallel
Up: Fast Vortex Algorithm
Previous: 12.5.2 Fast Algorithms
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
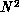 approach has made its parallel
implementation fairly straightforward (see [Fox:88a]). However,
as we have already seen in Section 12.4, that character was
drastically changed by the fast algorithm as it introduced a strong
component of locality. Globality is still present since the influence
of particle is felt throughout the domain, but more care and
computational effort is given to its near field. The fast parallel
algorithm has to reflect that dual nature, otherwise an efficient
implementation will never be obtained. Moreover, the domain
decomposition can no longer ignore the spatial distribution of the
vortices. Nearby vortices are strongly coupled computationally, so it
makes sense to assign them to the same processor. Binary bisection is
used in the host to spatially decompose the domain. Then, only the
vortices are sent to the processors where a binary tree is locally
built on top of them. For example, Figure 12.17 shows the
portion of the data structure assigned to processor 1 in a
4-processor environment.
approach has made its parallel
implementation fairly straightforward (see [Fox:88a]). However,
as we have already seen in Section 12.4, that character was
drastically changed by the fast algorithm as it introduced a strong
component of locality. Globality is still present since the influence
of particle is felt throughout the domain, but more care and
computational effort is given to its near field. The fast parallel
algorithm has to reflect that dual nature, otherwise an efficient
implementation will never be obtained. Moreover, the domain
decomposition can no longer ignore the spatial distribution of the
vortices. Nearby vortices are strongly coupled computationally, so it
makes sense to assign them to the same processor. Binary bisection is
used in the host to spatially decompose the domain. Then, only the
vortices are sent to the processors where a binary tree is locally
built on top of them. For example, Figure 12.17 shows the
portion of the data structure assigned to processor 1 in a
4-processor environment.






