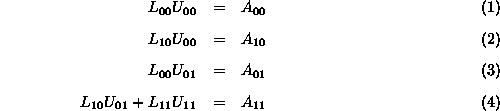
where
Suppose the ![]() matrix A is partitioned as shown in Figure
5, and we seek a factorization A=LU, where the partitioning
of L and U is also shown in Figure 5. Then we may write,
matrix A is partitioned as shown in Figure
5, and we seek a factorization A=LU, where the partitioning
of L and U is also shown in Figure 5. Then we may write,
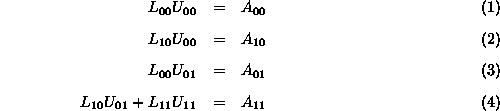
where ![]() is
is ![]() ,
, ![]() is
is ![]() ,
,
![]() is
is ![]() , and
, and ![]() is
is ![]() .
. ![]() and
and ![]() are lower triangular matrices with 1s on the main diagonal,
and
are lower triangular matrices with 1s on the main diagonal,
and ![]() and
and ![]() are upper triangular matrices.
are upper triangular matrices.
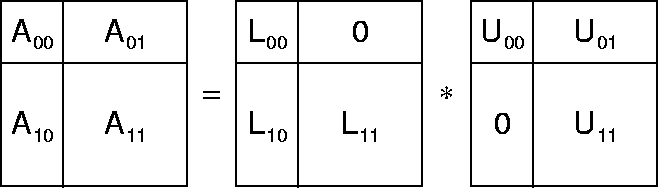
Figure 5: Block LU factorization of the partitioned matrix A. ![]() is
is
![]() ,
, ![]() is
is ![]() ,
, ![]() is
is ![]() ,
and
,
and ![]() is
is ![]() .
. ![]() and
and ![]() are
lower triangular matrices with 1's on the main diagonal,
and
are
lower triangular matrices with 1's on the main diagonal,
and ![]() and
and ![]() are upper triangular matrices.
are upper triangular matrices.
Equations 1 and 2 taken together perform an LU
factorization on the first ![]() panel of A (i.e.,
panel of A (i.e., ![]() and
and
![]() ). Once this is completed,
the matrices
). Once this is completed,
the matrices ![]() ,
, ![]() , and
, and ![]() are known, and the lower
triangular system in Eq. 3 can be solved to give
are known, and the lower
triangular system in Eq. 3 can be solved to give ![]() .
Finally, we rearrange Eq. 4 as,
.
Finally, we rearrange Eq. 4 as,
![]()
From this equation we see that the problem of finding ![]() and
and
![]() reduces to finding the LU factorization of the
reduces to finding the LU factorization of the
![]() matrix
matrix ![]() . This can be done by applying the steps
outlined above to
. This can be done by applying the steps
outlined above to ![]() instead of to A. Repeating these steps K times,
where
instead of to A. Repeating these steps K times,
where
![]()
where ![]() denotes the least integer greater than or equal to x,
we obtain the LU factorization of the original
denotes the least integer greater than or equal to x,
we obtain the LU factorization of the original ![]() matrix A. For
an in-place algorithm, A is overwritten by L and U - the 1s on the
diagonal of L do not need to be stored explicitly. Similarly,
when A is updated by Eq. 5 this may also be done in place.
matrix A. For
an in-place algorithm, A is overwritten by L and U - the 1s on the
diagonal of L do not need to be stored explicitly. Similarly,
when A is updated by Eq. 5 this may also be done in place.
After k of these K steps, the first kr columns of L and the first
kr rows of U have been evaluated, and matrix A has been updated to the
form shown in Figure 6, in which panel B is
![]() and C is
and C is ![]() . Step k+1 then
proceeds as follows,
. Step k+1 then
proceeds as follows,
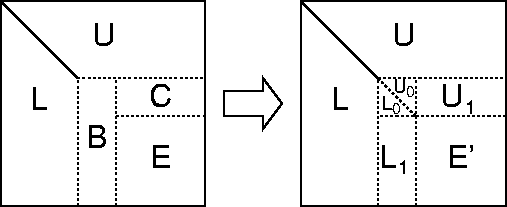
Figure 6: Stage k+1 of the block LU factorization algorithm showing
how the panels B and C, and the trailing submatrix E are updated.
The trapezoidal submatrices L and U have already been factored in
previous steps. L has kr columns, and U has kr rows. In the step
shown another r columns of L and r rows of U are evaluated.
The LAPACK implementation of this form of LU factorization uses the Level 3
BLAS routines xTRSM and xGEMM to perform the triangular solve and rank-r
update. We can regard the algorithm as acting on matrices that have been
partitioned into blocks of ![]() elements, as shown in Figure
7.
elements, as shown in Figure
7.

Figure 7: Block-partitioned matrix A. Each block ![]() consists of
consists of
![]() matrix elements.
matrix elements.