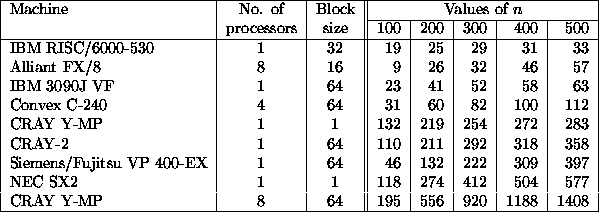
Table 3: Speed (Megaflops) of SGETRF/DGETRF for Square Matrices of Order n
Having discussed in detail the derivation of one particular block algorithm, we now describe examples of the performance achieved with two well-known block algorithms: LU and Cholesky factorizations. No extra floating-point operations nor extra working storage are required for either of these simple block algorithms. (See Gallivan et al. [31] and Dongarra et al. [19] for surveys of algorithms for dense linear algebra on high-performance computers.)
Table 3 illustrates the speed of the LAPACK routine for LU factorization of a real matrix, SGETRF in single precision on CRAY machines, and DGETRF in double precision on all other machines. Thus, 64-bit floating-point arithmetic is used on all machines tested. A block size of 1 means that the unblocked algorithm is used, since it is faster than - or at least as fast as - a block algorithm. In all cases, results are reported for the block size which is mostly nearly optimal over the range of problem sizes considered.
LAPACK is designed to give high efficiency on vector processors, high-performance ``superscalar'' workstations, and shared memory multiprocessors. LAPACK in its present form is less likely to give good performance on other types of parallel architectures (for example, massively parallel SIMD machines, or MIMD distributed memory machines), but the ScaLAPACK project, described in Section 1.1.4, is intended to adapt LAPACK to these new architectures. LAPACK can also be used satisfactorily on all types of scalar machines (PCs, workstations, mainframes).

Table 3: Speed (Megaflops) of SGETRF/DGETRF for Square Matrices of Order n
Table 4 gives similar results for Cholesky factorization, extending the results given in Table 2.
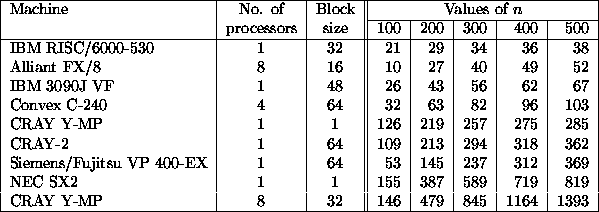
Table 4: Speed (Megaflops) of SPOTRF/DPOTRF for Matrices of Order n.
Here UPLO = `U', so the factorization is of the form ![]() .
.
LAPACK, like LINPACK, provides LU and Cholesky factorizations of band matrices. The LINPACK algorithms can easily be restructured to use Level 2 BLAS, though restructuring has little effect on performance for matrices of very narrow bandwidth. It is also possible to use Level 3 BLAS, at the price of doing some extra work with zero elements outside the band [21]. This process becomes worthwhile for large matrices and semi-bandwidth greater than 100 or so.