To derive a block form of Cholesky
factorization, we partition the matrices as shown in Figure
4, in which the diagonal blocks of A and U are square,
but of differing sizes. We assume that the first block has already been
factored as 
, and that we now want to determine
the second block column of U consisting of the blocks 
and
.
Equating submatrices in the second block of columns, we obtain
Hence, since 
has already been computed, we can compute as
the solution to the equation
by a call to the Level 3 BLAS routine STRSM; and then we can compute
from
This involves first updating the symmetric submatrix 
by a call to the
Level 3 BLAS routine SSYRK, and then computing its Cholesky factorization.
Since Fortran 77 does not allow recursion, a separate routine must be called
(using Level 2 BLAS rather than Level 3), named SPOTF2 in Figure
3.
In this way, successive blocks of columns of U are computed.
The LAPACK-style code for the block algorithm is shown in Figure
3.
This code runs at 49 megaflops on an IBM 3090, more than double the speed of
the LINPACK code.
On a CRAY Y-MP, the use of Level 3 BLAS squeezes a little more performance
out of one processor, but makes a large improvement when using all 8
processors.
Table 2 summarizes the results.
Figure 3: The body of the ``LAPACK-style'' routine SPOFA for block Cholesky
factorization. In this code fragment, nb denotes the width of
the blocks.
Figure 2: The body of the ``LAPACK-style'' routine SPOFA for Cholesky
factorization.
Figure 1: The body of the LINPACK routine SPOFA for Cholesky factorization.
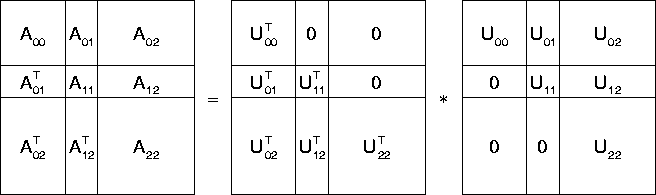
Figure 4: Partitioning of A, 
, and U into blocks. It is assumed that
the first block has already been factored as , and we
next want to determine the block column consisting of and .
Note that the diagonal blocks of A and U are square matrices.
Table 2: Speed (Megaflops) of Cholesky Factorization 
for n = 500