It is comparatively straightforward to recode many of the algorithms in
LINPACK and EISPACK so that they call Level 2 BLAS. Indeed, in the simplest
cases the same floating-point operations are done, possibly even in
the same order: it is just a matter of reorganizing the software.
To illustrate
this point, we
consider
the Cholesky factorization algorithm used in the
LINPACK routine SPOFA, which factorizes a symmetric positive definite matrix
as 
.
We consider Cholesky factorization because the algorithm is simple,
and no pivoting is required. In Section 4 we shall consider the
slightly more complicated example of LU factorization.
Suppose that after j-1 steps the block 
in the upper lefthand corner
of A has been factored as 
. The next row and column
of the factorization can then be computed by writing as
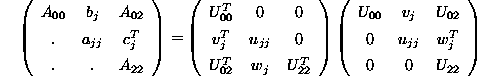
where 
, 
, 
, and 
are column vectors of length j-1, and
and 
are scalars.
Equating coefficients of the 
column, we obtain
Since 
has already been computed, we can compute and
from the equations
The body of the code of the LINPACK routine SPOFA that implements the above method is shown in Figure 1. The same computation recoded in ``LAPACK-style'' to use the Level 2 BLAS routine STRSV (which solves a triangular system of equations) is shown in Figure 2. The call to STRSV has replaced the loop over K which made several calls to the Level 1 BLAS routine SDOT. (For reasons given below, this is not the actual code used in LAPACK -- hence the term ``LAPACK-style''.)
This change by itself is sufficient to result in large gains in performance on a number of machines--for example, from 72 to 251 megaflops for a matrix of order 500 on one processor of a CRAY Y-MP. Since this is 81% of the peak speed of matrix-matrix multiplication on this processor, we cannot hope to do very much better by using Level 3 BLAS.
We can, however, restructure the algorithm at a deeper level to exploit the faster speed of the Level 3 BLAS. This restructuring involves recasting the algorithm as a block algorithm--that is, an algorithm that operates on blocks or submatrices of the original matrix.