




Next: 6.7.3 Conclusions
Up: An Adaptive Multiscale
Previous: 6.7.1 Errors in Computing
First, a Gaussian pyramid [Burt:84a] is
computed from the given images.
This consists of a hierarchy of images obtained filtering the original ones
with Gaussian filters of progressively larger size.
Then, the optical flow field is computed at the coarsest scale using
relaxation, and the estimated error is calculated for every pixel. If this
quantity is less than a given threshold 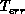 , the current value of the
flow is interpolated to the finer resolutions without further processing.
This is done by setting an inhibition flag contained in the grid
points of the pyramidal structure, so that these points do not participate in
the relaxation process. On the contrary, if the error is larger than
, the current value of the
flow is interpolated to the finer resolutions without further processing.
This is done by setting an inhibition flag contained in the grid
points of the pyramidal structure, so that these points do not participate in
the relaxation process. On the contrary, if the error is larger than
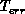 , the approximation is relaxed on a finer scale and the entire
process is repeated until the finest scale is reached.
, the approximation is relaxed on a finer scale and the entire
process is repeated until the finest scale is reached.
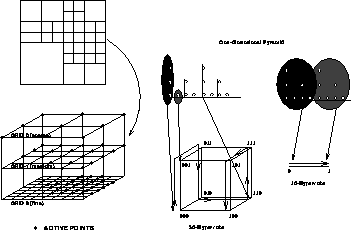
Figure 6.39: Adaptive Grid (shown on left) in the Multiresolution
Pyramid; (middle) Gray Code Mapping Strategy; (right) Domain
Decomposition Mapping Strategy. In the middle and right pictures, the
activity pattern for three resolutions is shown at the top, for a
simple one-dimensional case.
In this way, we obtain a local inhomogeneous approach where areas of
the images, characterized by different spatial frequencies or by different
motion amplitudes, are processed at the appropriate resolutions, avoiding
corruption of good estimates by inconsistent information from a different
scale (the effect shown in the previous example). The optimal grid
structure for a given image is translated into a pattern of active and
inhibited grid points in the pyramid, as
illustrated in Figure 6.39.
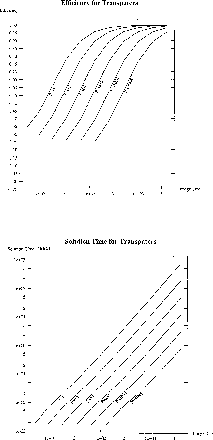
Figure 6.40: Efficiency and Solution Times
The motivation for freezing the motion field as soon as the error is
below threshold, is that the estimation of the error may itself
become incorrect at finer scales and, therefore, useless in the decision
process. It is important to point out that single-scale or homogeneous
approaches cannot adequately solve the above problem. Intuitively, what
happens in the adaptive multiscale approach is that the velocity is
frozen as soon as the spatial and temporal differences at a given
scale are big enough to avoid quantization errors, but small enough to avoid
errors in the use of discretized formulas. The only assumption made in this
scheme is that the largest motion in the scene can be reliably computed at
one of the used resolutions. If the images contain motion
discontinuities, line processes
(indicating the presence of these discontinuities) are necessary to
prevent smoothing where it is not desired (see [Battiti:90a] and
the contained references).
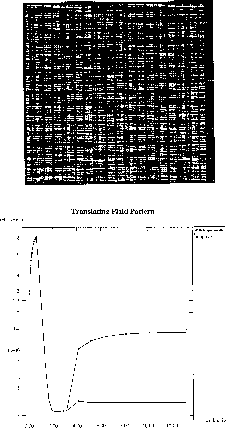
Figure 6.41: Plaid Image (top); The Error in Calculation of Optical Flow
for both Homogeneous (Upper-line) and Adaptive (Lower-line) Algorithms.
The error is plotted as a function of computation time.

Figure: Reconstructed Optical Flow for Translating ``Plaid'' Pattern
of Figure 6.41. Homogeneous Multiscale Strategy
(top), Adaptive Multiscale Strategy (middle), and Active (black) and
Inhibited (white) Points
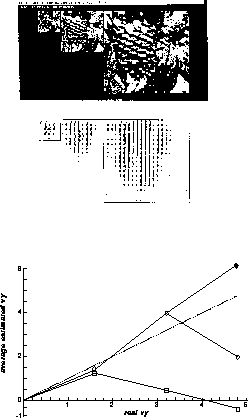
Figure 6.43: Test Images and Motion Fields for a Natural (pine-cone) Image
at Three Resolutions (top). Estimated versus Actual Velocity Plotted
for Three Choices of Resolution (bottom). The dotted line indicates a
``perfect'' prediction.
Large grain-size multicomputers, with a mapping based on domain
decomposition and limited coarsening, have been used to implement the
adaptive algorithm, as described in Section 6.5. The efficiency
and solution times for an implementation with
transputers (details in [Battiti:91a]) are
shown in Figure 6.40.
Real-time computation with high efficiency is within the reach of available
digital technology!
On a board with four transputers, and using the Express communication
routines from ParaSoft, the solution time for 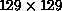 images is on
the order of one second.
images is on
the order of one second.
The software implementation is based on the multiscale vision environment
developed by Roberto Battiti and described in Section 9.9.
Christof Koch and Edoardo Amaldi collaborated on the project.





Next: 6.7.3 Conclusions
Up: An Adaptive Multiscale
Previous: 6.7.1 Errors in Computing
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
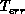 , the current value of the
flow is interpolated to the finer resolutions without further processing.
This is done by setting an inhibition flag contained in the grid
points of the pyramidal structure, so that these points do not participate in
the relaxation process. On the contrary, if the error is larger than
, the current value of the
flow is interpolated to the finer resolutions without further processing.
This is done by setting an inhibition flag contained in the grid
points of the pyramidal structure, so that these points do not participate in
the relaxation process. On the contrary, if the error is larger than
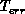 , the approximation is relaxed on a finer scale and the entire
process is repeated until the finest scale is reached.
, the approximation is relaxed on a finer scale and the entire
process is repeated until the finest scale is reached.










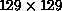 images is on
the order of one second.
images is on
the order of one second.