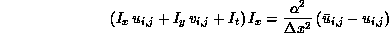





When moving objects in a scene are projected onto an image plane (for example, onto our retina), the real velocity field is transformed into a two-dimensional field, known as the motion field.
By taking more images at different times and calculating the motion field, we can extract useful parameters like the time to collision, useful for obstacle avoidance. If we know the motion of a camera (or our ego motion), we can reconstruct the entire three-dimensional structure of the environment (if the camera translates, near objects will have a larger motion field with respect to distant ones). The depth measurements can be used as starting constraints for a surface reconstruction algorithm like the one described in Section 9.9.
In particular situations, the apparent motion of the brightness pattern, known as the optical flow, provides a sufficiently accurate estimate of the motion field. Although the adaptive scheme that we propose is applicable to different methods, the discussion will be based on the scheme proposed by Horn and Schunck [Horn:81a]. They use the assumptions that the image brightness of a given point remains constant over time, and that the optical flow varies smoothly almost everywhere. Satisfaction of these two constraints is formulated as the problem of minimizing a quadratic energy functional (see also [Poggio:85a]). The appropriate Euler-Lagrange equations are then discretized on a single or multiple grid and solved using, for example, the Gauss-Seidel relaxation method [Horn:81a], [Terzopoulos:86a]). The resulting system of equations (two for every pixel in the image) is:
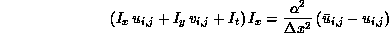
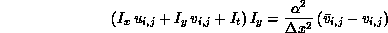
where 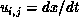 and
and 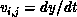 are the optical
flow variables to be determined,
are the optical
flow variables to be determined, 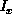 ,
, 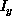 ,
, 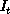 are the partial
derivatives of the image brightness with respect to space and time,
are the partial
derivatives of the image brightness with respect to space and time,  and
and  are local averages,
are local averages, 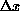 is the spatial discretization
step, and
is the spatial discretization
step, and  controls the smoothness of the estimated optical flow.
controls the smoothness of the estimated optical flow.
HPFA Applications




