




Next: An Adaptive Multiscale
Up: 6.6 Character Recognition by
Previous: 6.6.4 Results
Before closing, we would like to make some additional comments on the
multiscale method and suggest some possible extensions.
In a pattern-recognition problem such as character recognition, the
two-dimensional spatial structure of the
problem is important. The multiscale method preserves this structure
so that ``reasonable'' feature extractors are produced. An obvious
extension to the present work is to increase the number of hidden units
as one boosts the MLP to higher resolution. This corresponds to adding
completely new feature extractors. We did not do this in the present
case since 32 hidden units were sufficient-the problem of recognizing
upper-case Roman characters is too easy. For a more challenging
problem such as Chinese characters, adding hidden units will probably
be necessary. We should mention that incrementally adding hidden units
is easy to do and works well-we have used it to achieve perfect
convergence of a back-propagation network for the
problem of tic-tac-toe.
When boosting, the weights are scaled down by a factor of four and so it is
important to also scale down the learning rate (in the back-propagation
algorithm) by a factor of four.
We defined our ``blocking,'' or coarsening, procedure to
be a simple, grey scale averaging of 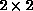 blocks. There are
many other possibilities, well known in the field of real-space
renormalization in physics. Other interesting blocking
procedures include: using a scale factor,
blocks. There are
many other possibilities, well known in the field of real-space
renormalization in physics. Other interesting blocking
procedures include: using a scale factor, 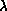 , different from
two; using majority rule averaging; simple decimation; and so on.
, different from
two; using majority rule averaging; simple decimation; and so on.
Multiscale methods work well in cases where spatial locality or smoothness
is relevant (otherwise, the interpolation approximation is bad). Another way
of thinking about this is that we are decomposing the problem onto a set of
spatially local basis functions such as gaussians. In other problems, a
different set of basis functions may be more appropriate and hence give better
performance.
The multiscale method uses results from a small net to help in the training
of a large network. The different-sized networks are related by the
rescaling or dilation operator. A variant of this general approach would be
to use the translation operator to produce a pattern matcher for the game of
Go. The idea is that at least some of the complexity of Go is
concerned with local strategies. Instead of training an MLP to learn this on
the full 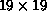 board of Go, do the training on a ``mini-Go'' board of
board of Go, do the training on a ``mini-Go'' board of
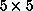 or
or 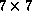 . The appropriate way to relate these networks to
the full-sized one is not through dilations, but via the translations: The
same local strategies are valid everywhere on the board.
. The appropriate way to relate these networks to
the full-sized one is not through dilations, but via the translations: The
same local strategies are valid everywhere on the board.
Steve Otto had the original idea for the MultiScale training technique. Otto
and Ed Felten and Olivier Martin developed the method. Jim Hutchinson
contributed by supplying the original back-propagation program.





Next: An Adaptive Multiscale
Up: 6.6 Character Recognition by
Previous: 6.6.4 Results
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
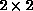 blocks. There are
many other possibilities, well known in the field of real-space
renormalization in physics. Other interesting blocking
procedures include: using a scale factor,
blocks. There are
many other possibilities, well known in the field of real-space
renormalization in physics. Other interesting blocking
procedures include: using a scale factor, 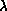 , different from
two; using majority rule averaging; simple decimation; and so on.
, different from
two; using majority rule averaging; simple decimation; and so on.





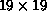 board of Go, do the training on a ``mini-Go'' board of
board of Go, do the training on a ``mini-Go'' board of
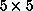 or
or 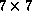 . The appropriate way to relate these networks to
the full-sized one is not through dilations, but via the translations: The
same local strategies are valid everywhere on the board.
. The appropriate way to relate these networks to
the full-sized one is not through dilations, but via the translations: The
same local strategies are valid everywhere on the board.