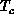 materials,
materials, 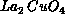 and
and
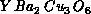 , despite the presence of large quantum fluctuations in
the spin-
, despite the presence of large quantum fluctuations in
the spin-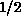 antiferromagnets.
antiferromagnets.





In this section, we discuss two further important developments based on the
previous section (Section 6.3) on the isotropic Heisenberg quantum
spins. These extensions are important in treating the observed phase
transitions
in the two-dimensional magnetic systems. Theoretically, two-dimensional
isotropic Heisenberg quantum spins remain in paramagnetic
state at all
temperatures [Mermin:66a]. However, all crystals found in nature with
strong two-dimensional magnetic characters go through phase transitions into
ordered states [Birgeneau:71a], [DeJongh:74a]. These include the
recently discovered high-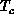 materials,
materials, 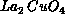 and
and
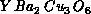 , despite the presence of large quantum fluctuations in
the spin-
, despite the presence of large quantum fluctuations in
the spin-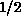 antiferromagnets.
antiferromagnets.
We consider the cases where the magnetic spins interact through
In the case  , the system goes through an Ising-like
antiferromagnetic transition, very similar to those that occur in the
high-
, the system goes through an Ising-like
antiferromagnetic transition, very similar to those that occur in the
high-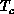 materials. In the case h = -J, that is, the XY model, the
system exhibits a Kosterlitz-Thouless type of transition. In both cases, our
simulation provides convincing and complete results for the first time.
materials. In the case h = -J, that is, the XY model, the
system exhibits a Kosterlitz-Thouless type of transition. In both cases, our
simulation provides convincing and complete results for the first time.
Through the Matsubara-Matsuda transformation between spin-1/2 operator
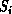 and bosonic creation/destruction operations
and bosonic creation/destruction operations 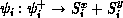 and
and 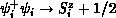 ,
a general quantum system can be mapped into quantum spin
system. Therefore, the phase transitions described here apply to
general two-dimensional quantum systems. These results have broad
implications in two-dimensional physical systems in particular, and the
statistical systems in general.
,
a general quantum system can be mapped into quantum spin
system. Therefore, the phase transitions described here apply to
general two-dimensional quantum systems. These results have broad
implications in two-dimensional physical systems in particular, and the
statistical systems in general.
HPFA Applications and Paradigms