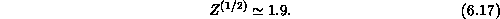Next: Comparison with Experiments
Up: 6.4.1 The case of
Previous: Simulation Results
It may seem a little surprising that a very small anisotropy can lead to a
substantially high 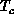 . This may be explained by the following argument.
At low T, the spins are highly correlated in the isotropic case. Since no
direction is preferred, the correlated spins fluctuate in all directions,
resulting in zero net magnetization. Adding a very small anisotropy into the
system introduces a preferred direction, so that the already highly
correlated spins will fluctuate around this direction, leading to a global
magnetization.
. This may be explained by the following argument.
At low T, the spins are highly correlated in the isotropic case. Since no
direction is preferred, the correlated spins fluctuate in all directions,
resulting in zero net magnetization. Adding a very small anisotropy into the
system introduces a preferred direction, so that the already highly
correlated spins will fluctuate around this direction, leading to a global
magnetization.
More quantitatively, the crossover from the isotropic Heisenberg behavior to
the Ising behavior occurs at 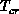 , where the correlation length is of
order of some power of the inverse anisotropy. From the scaling
arguments [Riedel:69a],
, where the correlation length is of
order of some power of the inverse anisotropy. From the scaling
arguments [Riedel:69a], 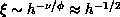 where
where 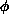 is the crossover exponent. In the two-dimensional model, both
is the crossover exponent. In the two-dimensional model, both
 and
and 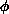 are infinite, but the ratio is approximately 1/2. For
are infinite, but the ratio is approximately 1/2. For
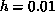 , this relation indicates that the Ising behavior is valid for
, this relation indicates that the Ising behavior is valid for
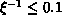 , which is clearly observed in Figure 6.16.
Similar crossover around
, which is clearly observed in Figure 6.16.
Similar crossover around 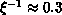 for
for 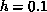 is also
observed in Figure 6.16. At low T, for the isotropic quantum
model, the correlation length behaves as [Ding:90g]
is also
observed in Figure 6.16. At low T, for the isotropic quantum
model, the correlation length behaves as [Ding:90g]
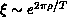 where
where 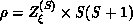 . Therefore,
we expect
. Therefore,
we expect
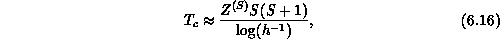
where 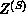 is spin-S dependent constant of order one.
Therefore, even a very small anisotropy
is spin-S dependent constant of order one.
Therefore, even a very small anisotropy 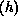 will induce a phase
transition at a substantially high temperature
(
will induce a phase
transition at a substantially high temperature
(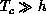 ). This crude picture, suggested a long time ago to
explain the observed phase transitions, is now confirmed by the
extensive quantum Monte Carlo simulations for the
first time. Note that this problem is an extreme case both because it
is an antiferromagnet (more difficult to become ordered than the
ferromagnet), and because it has the largest quantum fluctuations
(spin-
). This crude picture, suggested a long time ago to
explain the observed phase transitions, is now confirmed by the
extensive quantum Monte Carlo simulations for the
first time. Note that this problem is an extreme case both because it
is an antiferromagnet (more difficult to become ordered than the
ferromagnet), and because it has the largest quantum fluctuations
(spin-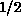 ). Since
). Since 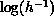 varies slowly with h, we can
estimate
varies slowly with h, we can
estimate 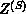 at
at 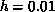 :
:
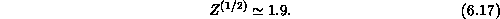





Next: Comparison with Experiments
Up: 6.4.1 The case of
Previous: Simulation Results
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
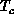 . This may be explained by the following argument.
At low T, the spins are highly correlated in the isotropic case. Since no
direction is preferred, the correlated spins fluctuate in all directions,
resulting in zero net magnetization. Adding a very small anisotropy into the
system introduces a preferred direction, so that the already highly
correlated spins will fluctuate around this direction, leading to a global
magnetization.
. This may be explained by the following argument.
At low T, the spins are highly correlated in the isotropic case. Since no
direction is preferred, the correlated spins fluctuate in all directions,
resulting in zero net magnetization. Adding a very small anisotropy into the
system introduces a preferred direction, so that the already highly
correlated spins will fluctuate around this direction, leading to a global
magnetization.





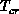 , where the correlation length is of
order of some power of the inverse anisotropy. From the scaling
arguments [
, where the correlation length is of
order of some power of the inverse anisotropy. From the scaling
arguments [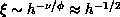 where
where 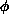 is the crossover exponent. In the two-dimensional model, both
is the crossover exponent. In the two-dimensional model, both
 and
and 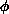 are infinite, but the ratio is approximately 1/2. For
are infinite, but the ratio is approximately 1/2. For
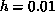 , this relation indicates that the Ising behavior is valid for
, this relation indicates that the Ising behavior is valid for
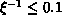 , which is clearly observed in Figure
, which is clearly observed in Figure 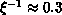 for
for 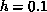 is also
observed in Figure
is also
observed in Figure 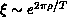 where
where 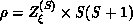 . Therefore,
we expect
. Therefore,
we expect
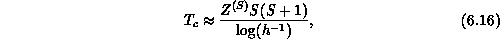
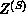 is spin-S dependent constant of order one.
Therefore, even a very small anisotropy
is spin-S dependent constant of order one.
Therefore, even a very small anisotropy 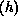 will induce a phase
transition
will induce a phase
transition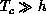 ). This crude picture, suggested a long time ago to
explain the observed phase transitions, is now confirmed by the
extensive quantum Monte Carlo
). This crude picture, suggested a long time ago to
explain the observed phase transitions, is now confirmed by the
extensive quantum Monte Carlo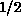 ). Since
). Since 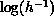 varies slowly with h, we can
estimate
varies slowly with h, we can
estimate 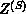 at
at 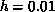 :
: