




Next: The Case of
Up: 6.4.1 The case of
Previous: Theoretical Interpretation
This simple result correctly predicts 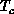 for a wide class of
crystals found in nature, assuming the same level of anisotropy, that
is,
for a wide class of
crystals found in nature, assuming the same level of anisotropy, that
is, 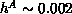 . The high-
. The high-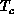 superconductor
superconductor
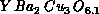 exhibits a Néel
transition at
exhibits a Néel
transition at 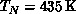 . With
. With 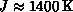 , our results give quite a close estimate:
, our results give quite a close estimate:
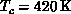 . Similar close predictions hold for other
. Similar close predictions hold for other
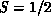 systems, such as superconductor
systems, such as superconductor 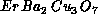 and
insulator
and
insulator 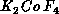 . For the high-
. For the high-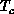 material
material 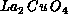 ,
,
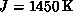 [Ding:90g]. This material undergoes a Néel
transition at
[Ding:90g]. This material undergoes a Néel
transition at 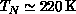 . Our prediction of
. Our prediction of 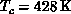 is in the same range of
is in the same range of 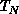 , and much better than the
naive expectation that
, and much better than the
naive expectation that 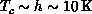 . In this
crystal, there is some degree of frustration (see
below), so the actual transition is pushed down. These examples
clearly indicate that the in-plane anisotropy could be quite important
to bring the system to the Néel order for these high-
. In this
crystal, there is some degree of frustration (see
below), so the actual transition is pushed down. These examples
clearly indicate that the in-plane anisotropy could be quite important
to bring the system to the Néel order for these high-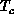 materials. For the S=1 system,
materials. For the S=1 system, 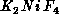 , our results predict a
, our results predict a
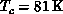 , quite close to the observed
, quite close to the observed 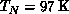 .
.
These results have direct consequences regarding the critical
exponents. The onset of transition is
entirely due to the Ising-like anisotropy. Once the system becomes
Néel-ordered, different layers in the three-dimensional crystals will
order at the same time. Spin fluctuations, in different layers, are
incoherent so that the critical exponents such as 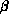 ,
, 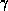 ,
and
,
and  will be the two, rather than three-dimensional Ising
exponents.
will be the two, rather than three-dimensional Ising
exponents. 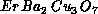 and
and 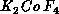 show such
behaviors clearly. However, the interlayer coupling, although very
small (much smaller than the in-plane anisotropy), could induce
coherent correlations between the layers, so that the critical
exponents will be somewhere between the two and three-dimensional Ising
exponents.
show such
behaviors clearly. However, the interlayer coupling, although very
small (much smaller than the in-plane anisotropy), could induce
coherent correlations between the layers, so that the critical
exponents will be somewhere between the two and three-dimensional Ising
exponents. 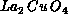 and
and 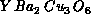 seem to belong to
this category.
seem to belong to
this category.
Whether the ground state of the spin-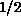 antiferromagnet spins has
the long-range Néel order, is a longstanding problem [Anderson:87a].
The existence of the Néel order is vigorously proved for
antiferromagnet spins has
the long-range Néel order, is a longstanding problem [Anderson:87a].
The existence of the Néel order is vigorously proved for 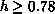 . In
the most interesting case
. In
the most interesting case 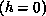 , numerical calculations on small lattices
suggested the existence of the long-range order. Our simulation establishes
the long-range order for
, numerical calculations on small lattices
suggested the existence of the long-range order. Our simulation establishes
the long-range order for 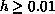 .
.
The fact that near 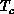 , the spin system is quite sensitive to the
tiny anisotropy could have a number of important consequences. For
example, the correlation lengths measured in
, the spin system is quite sensitive to the
tiny anisotropy could have a number of important consequences. For
example, the correlation lengths measured in 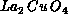 are
systematically smaller than the theoretical prediction [Ding:90g]
near
are
systematically smaller than the theoretical prediction [Ding:90g]
near 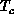 . The weaker correlations probably indicate that the
frustrations, due to the next to nearest neighbor interaction, come
into play. This is consistent with the fact that
. The weaker correlations probably indicate that the
frustrations, due to the next to nearest neighbor interaction, come
into play. This is consistent with the fact that 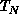 is below the
is below the
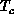 suggested by our results.
suggested by our results.





Next: The Case of
Up: 6.4.1 The case of
Previous: Theoretical Interpretation
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
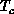 for a wide class of
crystals found in nature, assuming the same level of anisotropy, that
is,
for a wide class of
crystals found in nature, assuming the same level of anisotropy, that
is, 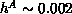 . The high-
. The high-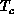 superconductor
superconductor
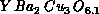 exhibits a Néel
transition at
exhibits a Néel
transition at 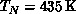 . With
. With 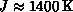 , our results give quite a close estimate:
, our results give quite a close estimate:
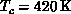 . Similar close predictions hold for other
. Similar close predictions hold for other
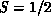 systems, such as superconductor
systems, such as superconductor 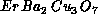 and
insulator
and
insulator 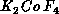 . For the high-
. For the high-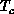 material
material 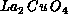 ,
,
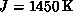 [Ding:90g]. This material undergoes a Néel
transition at
[Ding:90g]. This material undergoes a Néel
transition at 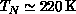 . Our prediction of
. Our prediction of 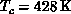 is in the same range of
is in the same range of 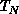 , and much better than the
naive expectation that
, and much better than the
naive expectation that 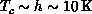 . In this
crystal, there is some degree of frustration (see
below), so the actual transition is pushed down. These examples
clearly indicate that the in-plane anisotropy could be quite important
to bring the system to the Néel order for these high-
. In this
crystal, there is some degree of frustration (see
below), so the actual transition is pushed down. These examples
clearly indicate that the in-plane anisotropy could be quite important
to bring the system to the Néel order for these high-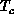 materials. For the S=1 system,
materials. For the S=1 system, 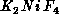 , our results predict a
, our results predict a
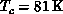 , quite close to the observed
, quite close to the observed 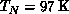 .
.





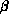 ,
, 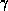 ,
and
,
and  will be the two, rather than three-dimensional Ising
exponents.
will be the two, rather than three-dimensional Ising
exponents. 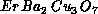 and
and 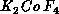 show such
behaviors clearly. However, the interlayer coupling, although very
small (much smaller than the in-plane anisotropy), could induce
coherent correlations between the layers, so that the critical
exponents will be somewhere between the two and three-dimensional Ising
exponents.
show such
behaviors clearly. However, the interlayer coupling, although very
small (much smaller than the in-plane anisotropy), could induce
coherent correlations between the layers, so that the critical
exponents will be somewhere between the two and three-dimensional Ising
exponents. 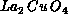 and
and 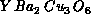 seem to belong to
this category.
seem to belong to
this category.
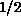 antiferromagnet spins has
the long-range Néel order, is a longstanding problem [
antiferromagnet spins has
the long-range Néel order, is a longstanding problem [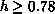 . In
the most interesting case
. In
the most interesting case 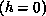 , numerical calculations on small lattices
suggested the existence of the long-range order. Our simulation establishes
the long-range order for
, numerical calculations on small lattices
suggested the existence of the long-range order. Our simulation establishes
the long-range order for 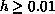 .
.
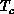 , the spin system is quite sensitive to the
tiny anisotropy could have a number of important consequences. For
example, the correlation lengths measured in
, the spin system is quite sensitive to the
tiny anisotropy could have a number of important consequences. For
example, the correlation lengths measured in 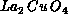 are
systematically smaller than the theoretical prediction [
are
systematically smaller than the theoretical prediction [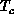 . The weaker correlations probably indicate that the
frustrations, due to the next to nearest neighbor interaction, come
into play. This is consistent with the fact that
. The weaker correlations probably indicate that the
frustrations, due to the next to nearest neighbor interaction, come
into play. This is consistent with the fact that 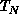 is below the
is below the
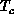 suggested by our results.
suggested by our results.