




Next: Implications
Up: The Case of
Previous: A Brief History
The key to pinning down the existence and type of transition is a study
of correlation length and in-plane susceptibility, because their
divergences constitute the most direct evidence of a phase transition.
These quantities are much more difficult to measure, and large lattices
are required in order to avoid finite size effects. These key points
are lacking in the previous works, and are the focus of our study. By
extensive use of the Mark IIIfp Hypercube, we are able to measure spin
correlations and thermodynamic quantities accurately on very large
lattices (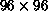 ). Our work
[Ding:90h;92a] provides convincing evidence that a phase transition
does occur at a finite temperature in the extreme quantum case, spin-
). Our work
[Ding:90h;92a] provides convincing evidence that a phase transition
does occur at a finite temperature in the extreme quantum case, spin-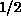 .
At transition point,
.
At transition point, 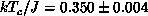 , the correlation length
and susceptibility diverge exactly according to the form of
Kosterlitz-Thouless (Equation 6.18).
, the correlation length
and susceptibility diverge exactly according to the form of
Kosterlitz-Thouless (Equation 6.18).
We plot the correlation length, 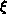 , and the susceptibility,
, and the susceptibility, 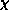 , in
Figures 6.18 and 6.19. They show a tendency of
divergence at some finite
, in
Figures 6.18 and 6.19. They show a tendency of
divergence at some finite 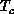 . Indeed, we fit them to the form predicted
by Kosterlitz and Thouless for the classical model
. Indeed, we fit them to the form predicted
by Kosterlitz and Thouless for the classical model
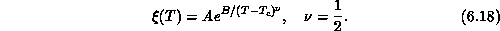
The fit is indeed very good (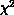 per degree of freedom is 0.81),
as shown in Figure 6.18. The fit for correlation length gives
per degree of freedom is 0.81),
as shown in Figure 6.18. The fit for correlation length gives
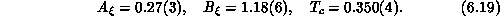
A similar fit for susceptibility, 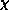 is also very good
(
is also very good
(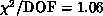 ):
):
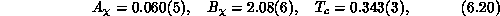
as shown in Figure 6.19. The good quality of both fits and the
closeness of 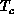 's obtained are the main results of this work. The fact
that these fits also reproduce the expected scaling behavior
's obtained are the main results of this work. The fact
that these fits also reproduce the expected scaling behavior 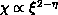 with
with
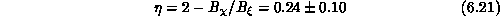
is a further consistency check. These results strongly indicate that the
spin-1/2 XY model undergoes a Kosterlitz-Thouless phase transition at
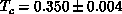 . We note that this
. We note that this 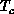 is consistent with the trend
of the ``twist energy'' [Loh:85a] and that the rapid increase of vortex
density near
is consistent with the trend
of the ``twist energy'' [Loh:85a] and that the rapid increase of vortex
density near 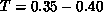 is due to the unbinding of vortex pairs.
Figures 6.18 and 6.19 also indicate that the
critical region
is due to the unbinding of vortex pairs.
Figures 6.18 and 6.19 also indicate that the
critical region 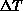 is quite wide (
is quite wide (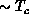 ), which is very similar
to the spin-1/2 Heisenberg model, where the
), which is very similar
to the spin-1/2 Heisenberg model, where the 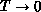 behavior holds
up to
behavior holds
up to 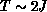 . These two-dimensional phenomena are in sharp contrast to
the usual second-order transitions in three dimensions.
. These two-dimensional phenomena are in sharp contrast to
the usual second-order transitions in three dimensions.
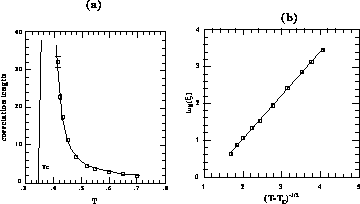
Figure 6.18: Correlation Length and Fit. (a) 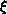 versus T. The vertical
line indicates
versus T. The vertical
line indicates 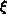 diverges at
diverges at 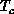 ; (b)
; (b) 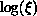 versus
versus
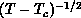 . The straight line indicates
. The straight line indicates 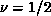 .
.
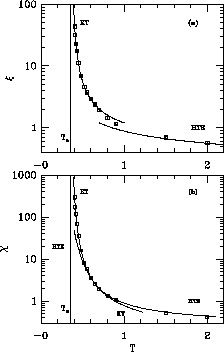
Figure: (a) This figure repeats the plot of Figure 6.18(a)
showing on a coarser scale both the high temperature expansion (HTE) and the
Kosterlitz-Thouless fit (KT). (b) Susceptibility 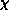 and Fit
and Fit
The algebraic exponent 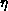 is consistent with the Ornstein-Zernike
exponent
is consistent with the Ornstein-Zernike
exponent 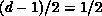 at higher T. As
at higher T. As 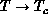 ,
, 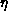 shifts
down slightly and shows signs of approaching 1/4, the value at
shifts
down slightly and shows signs of approaching 1/4, the value at 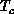 for the
classical model. This is consistent with Equation 6.21.
for the
classical model. This is consistent with Equation 6.21.
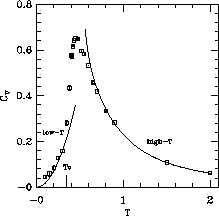
Figure 6.20: Specific Heat 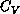 . For
. For 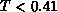 , the lattice size is
, the lattice size is
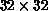 .
.
We measured energy and specific heat, 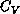 (for
(for 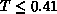 we used a
we used a
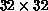 lattice). The specific heat is shown in
Figure 6.20. We found that
lattice). The specific heat is shown in
Figure 6.20. We found that 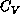 has a peak above
has a peak above 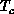 , at
around
, at
around 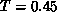 . The peak clearly shifts away from
. The peak clearly shifts away from 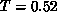 on the much
smaller
on the much
smaller 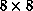 lattice. DeRaedt, et al. [DeRaedt:84a]
suggested a logarithmic divergent
lattice. DeRaedt, et al. [DeRaedt:84a]
suggested a logarithmic divergent 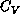 in their simulation, which is likely
an artifact of their small m values. One striking feature in
Figure 6.20 is a very steep increase of
in their simulation, which is likely
an artifact of their small m values. One striking feature in
Figure 6.20 is a very steep increase of 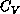 at
at 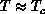 .
The shape of the curve is asymmetric near the peak. These features of the
.
The shape of the curve is asymmetric near the peak. These features of the
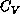 curve differ from that in the classical XY model [Gupta:88a].
curve differ from that in the classical XY model [Gupta:88a].





Next: Implications
Up: The Case of
Previous: A Brief History
Guy Robinson
Wed Mar 1 10:19:35 EST 1995
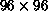 ). Our work
[Ding:90h;92a] provides convincing evidence that a phase transition
does occur at a finite temperature in the extreme quantum case, spin-
). Our work
[Ding:90h;92a] provides convincing evidence that a phase transition
does occur at a finite temperature in the extreme quantum case, spin-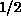 .
At transition point,
.
At transition point, 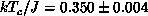 , the correlation length
and susceptibility diverge exactly according to the form of
Kosterlitz-Thouless (Equation 6.18).
, the correlation length
and susceptibility diverge exactly according to the form of
Kosterlitz-Thouless (Equation 6.18).





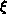 , and the susceptibility,
, and the susceptibility, 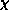 , in
Figures
, in
Figures 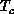 . Indeed, we fit them to the form predicted
by Kosterlitz and Thouless for the classical model
. Indeed, we fit them to the form predicted
by Kosterlitz and Thouless for the classical model
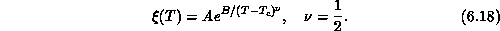
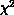 per degree of freedom is 0.81),
as shown in Figure
per degree of freedom is 0.81),
as shown in Figure 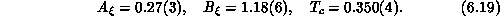
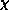 is also very good
(
is also very good
(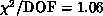 ):
):
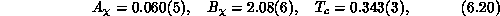
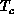 's obtained are the main results of this work. The fact
that these fits also reproduce the expected scaling behavior
's obtained are the main results of this work. The fact
that these fits also reproduce the expected scaling behavior 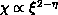 with
with
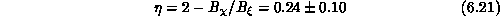
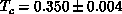 . We note that this
. We note that this 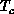 is consistent with the trend
of the ``twist energy'' [
is consistent with the trend
of the ``twist energy'' [ is due to the unbinding of vortex pairs.
Figures
is due to the unbinding of vortex pairs.
Figures 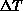 is quite wide (
is quite wide (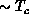 ), which is very similar
to the spin-1/2 Heisenberg model, where the
), which is very similar
to the spin-1/2 Heisenberg model, where the 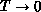 behavior holds
up to
behavior holds
up to 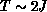 . These two-dimensional phenomena are in sharp contrast to
the usual second-order transitions in three dimensions.
. These two-dimensional phenomena are in sharp contrast to
the usual second-order transitions in three dimensions.

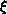 versus T. The vertical
line indicates
versus T. The vertical
line indicates 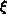 diverges at
diverges at 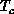 ; (b)
; (b) 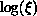 versus
versus
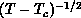 . The straight line indicates
. The straight line indicates 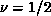 .
.
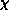 and Fit
and Fit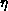 is consistent with the Ornstein-Zernike
exponent
is consistent with the Ornstein-Zernike
exponent 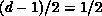 at higher T. As
at higher T. As 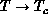 ,
, 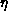 shifts
down slightly and shows signs of approaching 1/4, the value at
shifts
down slightly and shows signs of approaching 1/4, the value at 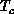 for the
classical model. This is consistent with Equation
for the
classical model. This is consistent with Equation 
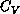 . For
. For 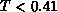 , the lattice size is
, the lattice size is
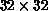 .
.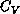 (for
(for 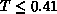 we used a
we used a
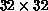 lattice). The specific heat is shown in
Figure
lattice). The specific heat is shown in
Figure 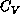 has a peak above
has a peak above 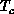 , at
around
, at
around 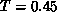 . The peak clearly shifts away from
. The peak clearly shifts away from 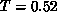 on the much
smaller
on the much
smaller 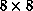 lattice. DeRaedt, et al. [
lattice. DeRaedt, et al. [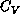 in their simulation, which is likely
an artifact of their small m values. One striking feature in
Figure
in their simulation, which is likely
an artifact of their small m values. One striking feature in
Figure 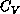 at
at 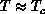 .
The shape of the curve is asymmetric near the peak. These features of the
.
The shape of the curve is asymmetric near the peak. These features of the
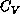 curve differ from that in the classical XY model [
curve differ from that in the classical XY model [