With the notion of a gradient and a notion of movement that respects the constraints of the manifold, one might wish to begin with an optimization routine of some sort. A steepest descent could be implemented from these alone. However, in order to carry out sophisticated optimizations, one usually wants some sort of second derivative information about the function.
In particular, one might wish to know by how much one can expect the
gradient to change if one moves from ![]() to
to ![]() . This can
actually be a difficult question to answer on a manifold.
Technically, the gradient at
. This can
actually be a difficult question to answer on a manifold.
Technically, the gradient at ![]() is a member of
is a member of
![]() ,
while the gradient at
,
while the gradient at ![]() is a member of
is a member of
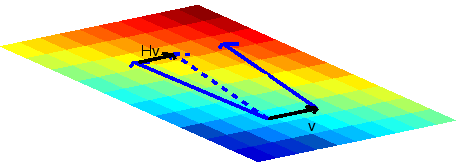
![]() . While taking their difference would work
fine in a flat space (see Figure 9.8), if this
were done on a curved space, it could give a vector
which is not a member of the tangent space of either point
(see Figure 9.9).
. While taking their difference would work
fine in a flat space (see Figure 9.8), if this
were done on a curved space, it could give a vector
which is not a member of the tangent space of either point
(see Figure 9.9).
 |
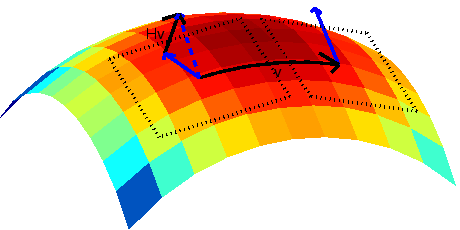 |
A more sophisticated means of taking this difference is to first
move the gradient at ![]() to
to ![]() in some manner which
translates it in a parallel fashion from
in some manner which
translates it in a parallel fashion from ![]() to
to ![]() , and
then compare the two gradients within the same tangent space. One
can check that for
, and
then compare the two gradients within the same tangent space. One
can check that for
![]() the rule
the rule
Using this rule to compare nearby vectors to each other, one then has
the following rule for taking derivatives of vector fields:
dgrad
in the software.
In an unconstrained minimization, the second derivative of the
gradient ![]() along a vector
along a vector ![]() is the Hessian
is the Hessian
![]() times
times ![]() .
Covariantly, we then have the analogy,
.
Covariantly, we then have the analogy,