We've now laid the groundwork for a meaningful definition of the
gradient in the setting of a constraint manifold. At this point, one
could run off and try to do a steepest descent search to maximize
one's objective functions. Trouble will arise, however, when one
discovers that there is no sensible way to combine a point and a
displacement to produce a new point because, for finite ![]() ,
, ![]() violates the constraint equations and thus does not give a point on
the manifold.
violates the constraint equations and thus does not give a point on
the manifold.
For any manifold, one updates ![]() by solving a set of differential
equations of motion
of the form
by solving a set of differential
equations of motion
of the form
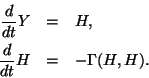
To see how these equations could be satisfied,
we take the infinitesimal constraint equation for ![]() ,
,
In the next subsection, we will have reason to consider
![]() for
for ![]() .
For technical reasons, one usually requests that
.
For technical reasons, one usually requests that
The connection for the Stiefel manifold using two different inner products
(the Euclidean and the canonical) can be found in the work by Edelman,
Arias, and Smith (see [151,155,416]). The function connection
computes
![]() in the template software.
in the template software.
Usually the solution of the equations of motions on a manifold are
very difficult to carry out. For the Stiefel manifold,
analytic solutions exist and can be found in the aforementioned
literature, though we have found very little performance
degradation between moving along paths via the equations of motion and
simply performing some orthogonalizing factorization on ![]() ,
as long as the displacements are small. The
,
as long as the displacements are small. The move function
supports multiple methods of geodesic motion, depending on the degree
of approximation desired.