Inner Products, Gradients, and Differentials

In flat spaces, we often identify the differential of a function with its gradient. However, when dealing with a more general setting, one can run into problems making sense out of such a definition.

For example, the gradient is a vector, and it should be possible to think of vectors as infinitesimal displacements of points. In $\mbox{Stief}(n,k)$, any infinitesimal displacement $\delta Y$ must satisfy $\delta Y^* Y + Y^* \delta Y = 0$. Thus, $df$ may not always be a vector, since it does not necessarily satisfy this equation. A gradient should be an infinitesimal displacement that points in the direction of the displacement which will give the greatest increase in $f$.

If the tangent space has an inner product, though, one can find a useful way to identify the $df$ uniquely with a tangent vector. Let $ip(H_1,H_2)$ be a symmetric nondegenerate bilinear form on the tangent space of $\mbox{Stief}(n,k)$ at $Y$. Then one can define the gradient, $G$, implicitly by

$$ip(G,H) = \tr ( H^* df) = D_H f.$$

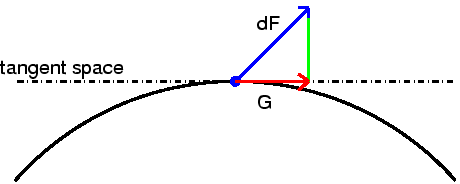
Since $ip$ is a nondegenerate form, this is sufficient to define $G$. The function tangent carries out this projection from differentials to tangents (shown in Figure 9.7). This operation is performed by grad to produce the gradient of the objective function.

Figure 9.7: The unconstrained differential of $F(Y)$ can be projected to the tangent space to obtain the covariant gradient, $G$, of $F$.