




Next: Example 8.6.1.
Up: Symmetric Indefinite Lanczos Method
Previous: Software Availability
Contents
Index
We present several examples which illustrate some of the features of the
symmetric indefinite Lanczos procedure described above.
In particular, the examples below illustrate three points:
- When
 is singular, premultiplying the starting vector by
is singular, premultiplying the starting vector by
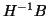 provides a dramatic improvement in the quality of the
computed Ritz pairs.
provides a dramatic improvement in the quality of the
computed Ritz pairs.
- When
 is singular, the postprocessing step described in equation
(8.27) may further improve the Ritz pairs.
is singular, the postprocessing step described in equation
(8.27) may further improve the Ritz pairs.
- Partial reorthogonalization provides substantial savings over complete
reorthogonalization.
In each of our example problems, the symmetric indefinite
eigenvalue problem stems from the linearization of a quadratic eigenvalue
problem which arises in structural dynamics.
The matrices come from one of two finite element models generated by
the structural engineering package MSC/NASTRAN [274].
All of the examples were run on a Sun UltraSPARC with a 336 MHz
processor using a simple MATLAB implementation of Algorithm 8.4.
Ritz values were accepted as ``converged'' based on the error bound
derived in §8.6.3. The bound was found to be
pessimistic in most cases, and a reliable tighter bound is still an open
research topic.
The first model is an acoustics problem representing a speaker box.
Two sets of matrices have been generated from the model. In the first set,
the linearized problem 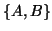 has order 1076.
In a smaller second set of matrices, modal reduction has been employed and
the associated matrices
has order 1076.
In a smaller second set of matrices, modal reduction has been employed and
the associated matrices 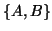 have order 668.
have order 668.
The second model represents a
shaft on bearing supports with a translational viscous damper attached at the
midpoint of the shaft. By controlling the mesh size, two
sets of matrices have been produced for this model. With a finer mesh, the
order of 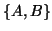 is 800, while a coarser mesh yields matrices
is 800, while a coarser mesh yields matrices 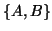 with
order 160. In each case, the resulting
with
order 160. In each case, the resulting  matrix is singular with this model.
matrix is singular with this model.
Subsections





Next: Example 8.6.1.
Up: Symmetric Indefinite Lanczos Method
Previous: Software Availability
Contents
Index
Susan Blackford
2000-11-20
![]() has order 1076.
In a smaller second set of matrices, modal reduction has been employed and
the associated matrices
has order 1076.
In a smaller second set of matrices, modal reduction has been employed and
the associated matrices ![]() have order 668.
have order 668.
![]() is 800, while a coarser mesh yields matrices
is 800, while a coarser mesh yields matrices ![]() with
order 160. In each case, the resulting
with
order 160. In each case, the resulting ![]() matrix is singular with this model.
matrix is singular with this model.