




Next: Generalized Hermitian Eigenproblems
Up: Hermitian Eigenproblems J.
Previous: Related Eigenproblems
Contents
Index
Example
For the vibrating mass-spring system introduced in §2.1 and
Figure 2.1, we assume that
- all masses
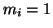 , so
, so 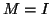 , and
, and
- all damping constants
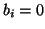 , so
, so 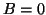 .
.
This simplies the equations of motion to
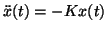 .
We solve them by substituting
.
We solve them by substituting
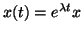 , where
, where 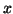 is
a constant vector and
is
a constant vector and  is a constant scalar to be determined.
This yields
is a constant scalar to be determined.
This yields
Thus 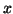 is an eigenvector
and
is an eigenvector
and 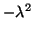 is an eigenvalue of the symmetric positive
definite tridiagonal matrix
is an eigenvalue of the symmetric positive
definite tridiagonal matrix 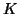 . Thus
. Thus  is pure imaginary
and we get that
is pure imaginary
and we get that 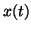 is periodic with period
is periodic with period
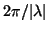 .
Symmetric tridiagonal matrices have particularly fast and efficient
eigenvalue algorithms.
.
Symmetric tridiagonal matrices have particularly fast and efficient
eigenvalue algorithms.
Later sections deal with the cases of nonunit masses 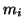 and nonzero damping constants
and nonzero damping constants 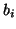 .
.
Susan Blackford
2000-11-20
![]() and nonzero damping constants
and nonzero damping constants ![]() .
.