




Next: Example
Up: Hermitian Eigenproblems J.
Previous: Specifying an Eigenproblem
Contents
Index
Related Eigenproblems
Since the HEP is one of the best understood
eigenproblems, it is helpful to recognize when other eigenproblems
can be converted to it.
- If
 is non-Hermitian, but
is non-Hermitian, but
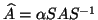 is
Hermitian for easily determined
is
Hermitian for easily determined 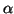 and
and 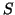 ,
it may be advisable
to compute the eigenvalues
,
it may be advisable
to compute the eigenvalues 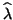 and eigenvectors
and eigenvectors 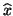 of
of 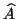 .
One can convert these to eigenvalues
.
One can convert these to eigenvalues  and eigenvectors
and eigenvectors 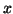 of
of  via
via
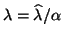 and
and
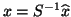 .
For example, multiplying a skew-Hermitian matrix
.
For example, multiplying a skew-Hermitian matrix  (i.e.,
(i.e., 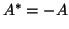 )
by the constant
)
by the constant 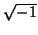 makes it Hermitian.
See §2.5
for further discussion.
makes it Hermitian.
See §2.5
for further discussion.
- If
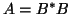 for some rectangular matrix
for some rectangular matrix  , then the eigenproblem
for
, then the eigenproblem
for  is equivalent to the SVD of
is equivalent to the SVD of  , discussed
in §2.4.
Suppose
, discussed
in §2.4.
Suppose  is
is  by
by  , so
, so  is
is  by
by  .
Generally speaking, if
.
Generally speaking, if  is about as small or smaller than
is about as small or smaller than  (
(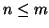 , or just a little bigger), the eigenproblem for
, or just a little bigger), the eigenproblem for  is
usually cheaper than the SVD of
is
usually cheaper than the SVD of  . But it may be less accurate to compute
the small eigenvalues of
. But it may be less accurate to compute
the small eigenvalues of  than the small singular values of
than the small singular values of  .
See §2.4
for further discussion.
.
See §2.4
for further discussion.
- If one has the generalized HEP
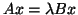 ,
where
,
where  and
and  are Hermitian and
are Hermitian and  is positive definite,
it can be converted to a Hermitian eigenproblem as follows.
First, factor
is positive definite,
it can be converted to a Hermitian eigenproblem as follows.
First, factor 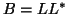 , where
, where 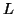 is any nonsingular matrix (this is
typically done using Cholesky factorization). Then solve the HEP
for
is any nonsingular matrix (this is
typically done using Cholesky factorization). Then solve the HEP
for
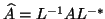 . The eigenvalues of
. The eigenvalues of
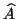 and
and 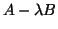 are identical, and if
are identical, and if 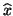 is an
eigenvector of
is an
eigenvector of 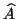 , then
, then
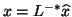 satisfies
satisfies
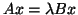 .
See §2.3
for further discussion.
.
See §2.3
for further discussion.





Next: Example
Up: Hermitian Eigenproblems J.
Previous: Specifying an Eigenproblem
Contents
Index
Susan Blackford
2000-11-20