




Next: Algorithm
Up: Lanczos Method for Complex
Previous: Properties of Complex Symmetric
Contents
Index
While the complex symmetry of  has no effect on the eigenvalues
of
has no effect on the eigenvalues
of  , this particular structure can be exploited
to halve the work and storage requirements of the general
non-Hermitian Lanczos method
described in §7.8.
Indeed, while the non-Hermitian Lanczos method involves one
matrix-vector product with
, this particular structure can be exploited
to halve the work and storage requirements of the general
non-Hermitian Lanczos method
described in §7.8.
Indeed, while the non-Hermitian Lanczos method involves one
matrix-vector product with  and one with
and one with 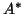 at each iteration,
the complex symmetric Lanczos method only requires one
matrix-vector product with
at each iteration,
the complex symmetric Lanczos method only requires one
matrix-vector product with  at each iteration.
at each iteration.
After  iterations, the complex symmetric Lanczos method
has generated
iterations, the complex symmetric Lanczos method
has generated  Lanczos vectors,
Lanczos vectors,
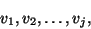 |
(200) |
that span the  th Krylov subspace
th Krylov subspace
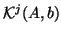 induced by
the complex symmetric matrix
induced by
the complex symmetric matrix  and any nonzero starting
vector
and any nonzero starting
vector 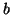 .
The vectors (7.94) are constructed to be complex orthogonal:
.
The vectors (7.94) are constructed to be complex orthogonal:
![\begin{displaymath}
V_j^T V_j = I_j,\quad \mbox{where}\quad
V_j = \left[ \begin{array}{cccc}
v_1 & v_2 & \cdots & v_j
\end{array} \right].
\end{displaymath}](img2506.png) |
(201) |
Note that, in view of the eigendecomposition (7.91)
of diagonalizable complex symmetric matrices  , the
complex orthogonality (7.95) of the Lanczos
vectors is natural.
, the
complex orthogonality (7.95) of the Lanczos
vectors is natural.
The complex symmetric Lanczos algorithm computes the
vectors (7.94) by means of three-term recurrences
that can be summarized as follows:
![\begin{displaymath}
A V_j = V_j T_j + \left[ \begin{array}{cccc}
0 & \cdots & 0 & \hat{v}_{j+1}
\end{array} \right].
\end{displaymath}](img2507.png) |
(202) |
Here,
![\begin{displaymath}
T_j = T_j^T = \left[ \begin{array}{cccc}
\alpha_1 & \beta_2...
...ots & \beta_j \\
& & \beta_j & \alpha_j
\end{array} \right]
\end{displaymath}](img2508.png) |
(203) |
is a complex symmetric tridiagonal matrix whose entries are
the coefficients of the three-term recurrences.
The vector 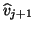 is the candidate for the next Lanczos
vector,
is the candidate for the next Lanczos
vector, 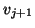 .
It is constructed so that the orthogonality condition
.
It is constructed so that the orthogonality condition
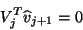 |
(204) |
is satisfied, and it only remains to be normalized so that
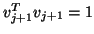 .
However, it cannot be excluded that
.
However, it cannot be excluded that
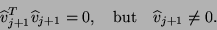 |
(205) |
If (7.99) occurs, then a next vector 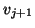 cannot
be obtained by simply normalizing
cannot
be obtained by simply normalizing 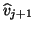 , as it would
require division by zero.
Therefore, (7.99) is called a breakdown
of the complex symmetric Lanczos algorithm.
Breakdowns can be remedied by incorporating look-ahead
into the algorithm.
Here, for simplicity, we restrict ourselves to the complex
symmetric Lanczos algorithm without look-ahead, and we simply
stop the algorithm in case a breakdown (7.99) is encountered.
, as it would
require division by zero.
Therefore, (7.99) is called a breakdown
of the complex symmetric Lanczos algorithm.
Breakdowns can be remedied by incorporating look-ahead
into the algorithm.
Here, for simplicity, we restrict ourselves to the complex
symmetric Lanczos algorithm without look-ahead, and we simply
stop the algorithm in case a breakdown (7.99) is encountered.
After  iterations of the complex symmetric Lanczos algorithm,
approximate eigensolutions for the complex symmetric
eigenvalue problem (7.88) are obtained by
computing eigensolutions of
iterations of the complex symmetric Lanczos algorithm,
approximate eigensolutions for the complex symmetric
eigenvalue problem (7.88) are obtained by
computing eigensolutions of 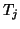 ,
,
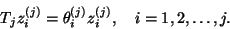 |
(206) |
Each value
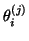 and its Ritz vector,
and its Ritz vector,
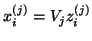 , yield an approximate eigenpair of
, yield an approximate eigenpair of  .
Note that
.
Note that 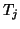 is the complex orthogonal projection of
is the complex orthogonal projection of  onto the space spanned by the Lanczos basis matrix
onto the space spanned by the Lanczos basis matrix 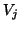 , i.e.,
, i.e.,
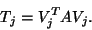 |
(207) |
Indeed, the relation follows by multiplying (7.96) from
the left by 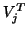 and by using the orthogonality
relations (7.95) and (7.98).
Of course, in the complex symmetric Lanczos algorithm, the
matrix
and by using the orthogonality
relations (7.95) and (7.98).
Of course, in the complex symmetric Lanczos algorithm, the
matrix 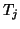 is not computed via the relation (7.101).
Instead, the symmetric tridiagonal structure in the
definition (7.97) is exploited and only the
diagonal and subdiagonal entries of
is not computed via the relation (7.101).
Instead, the symmetric tridiagonal structure in the
definition (7.97) is exploited and only the
diagonal and subdiagonal entries of 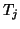 are explicitly
generated.
are explicitly
generated.
It should be pointed out that 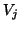 is
complex orthogonal, but not unitary, which may have effects
for the numerical stability.
is
complex orthogonal, but not unitary, which may have effects
for the numerical stability.





Next: Algorithm
Up: Lanczos Method for Complex
Previous: Properties of Complex Symmetric
Contents
Index
Susan Blackford
2000-11-20
![]() has no effect on the eigenvalues
of
has no effect on the eigenvalues
of ![]() , this particular structure can be exploited
to halve the work and storage requirements of the general
non-Hermitian Lanczos method
described in §7.8.
Indeed, while the non-Hermitian Lanczos method involves one
matrix-vector product with
, this particular structure can be exploited
to halve the work and storage requirements of the general
non-Hermitian Lanczos method
described in §7.8.
Indeed, while the non-Hermitian Lanczos method involves one
matrix-vector product with ![]() and one with
and one with ![]() at each iteration,
the complex symmetric Lanczos method only requires one
matrix-vector product with
at each iteration,
the complex symmetric Lanczos method only requires one
matrix-vector product with ![]() at each iteration.
at each iteration.
![]() iterations, the complex symmetric Lanczos method
has generated
iterations, the complex symmetric Lanczos method
has generated ![]() Lanczos vectors,
Lanczos vectors,
![]() iterations of the complex symmetric Lanczos algorithm,
approximate eigensolutions for the complex symmetric
eigenvalue problem (7.88) are obtained by
computing eigensolutions of
iterations of the complex symmetric Lanczos algorithm,
approximate eigensolutions for the complex symmetric
eigenvalue problem (7.88) are obtained by
computing eigensolutions of ![]() ,
,
![]() is
complex orthogonal, but not unitary, which may have effects
for the numerical stability.
is
complex orthogonal, but not unitary, which may have effects
for the numerical stability.