




Next: Properties of the Algorithm
Up: Lanczos Method for Complex
Previous: Lanczos Method for Complex
Contents
Index
Complex symmetry is a purely algebraic property, and it
has no effect on the spectrum of the matrix.
Indeed, for any given set of  numbers,
numbers,
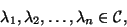 |
(195) |
there exists a complex symmetric  matrix
matrix  whose
eigenvalues are just the prescribed numbers (7.89);
see, e.g., [233, Theorem 4.4.9].
whose
eigenvalues are just the prescribed numbers (7.89);
see, e.g., [233, Theorem 4.4.9].
A complex symmetric matrix may not even be diagonalizable.
For example, consider the complex symmetric matrix
![\begin{displaymath}
A = \left[
\begin{array}{cc} 2 {\tt i} & 1\\
1 & 0
\end{array} \right],\quad
\mbox{where}\quad {\tt i} = \sqrt{-1}.
\end{displaymath}](img2494.png) |
(196) |
The only eigenvalue of this matrix is
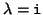 , with
algebraic multiplicity
, with
algebraic multiplicity 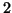 but geometric multiplicity
but geometric multiplicity 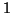 .
In fact, the Jordan normal form of
.
In fact, the Jordan normal form of  is as follows:
is as follows:
Thus,  is not diagonalizable.
is not diagonalizable.
If a complex symmetric matrix  is diagonalizable, then
it has an eigendecomposition that reflects the complex symmetry;
see, e.g., [233, Theorem 4.4.13].
More precisely, a complex symmetric matrix
is diagonalizable, then
it has an eigendecomposition that reflects the complex symmetry;
see, e.g., [233, Theorem 4.4.13].
More precisely, a complex symmetric matrix  is diagonalizable
if and only if its eigenvector matrix,
is diagonalizable
if and only if its eigenvector matrix,
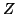 , can be chosen such that
, can be chosen such that
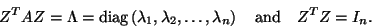 |
(197) |
A matrix 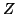 with
with  columns that satisfies
columns that satisfies 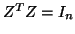 is
called complex orthogonal.
The complex orthogonality of
is
called complex orthogonal.
The complex orthogonality of 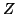 in (7.91) reflects the
complex symmetry of
in (7.91) reflects the
complex symmetry of  .
.
We remark that the eigendecomposition (7.91) is the
suitable adaptation of the corresponding decomposition for
Hermitian matrices.
Recall that for any matrix 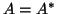 , the eigenvector matrix
, the eigenvector matrix
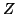 can always be chosen to be unitary:
can always be chosen to be unitary:
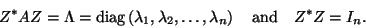 |
(198) |
The unitariness of 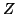 in (7.92) reflects the fact
that
in (7.92) reflects the fact
that  is Hermitian.
is Hermitian.
The reason why an eigendecomposition (7.91) does not
always exist is that there are complex vectors 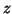 with
with
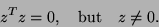 |
(199) |
Indeed, suppose  has an eigenvalue with a one-dimensional eigenspace
and the vector
has an eigenvalue with a one-dimensional eigenspace
and the vector 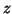 spanning that space satisfies (7.93).
Then one of the columns of any eigenvector matrix
spanning that space satisfies (7.93).
Then one of the columns of any eigenvector matrix 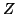 of
of  would be
of the form
would be
of the form
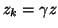 , where
, where 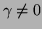 is a scalar.
Then, by (7.93),
is a scalar.
Then, by (7.93), 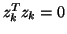 , while the
complex orthogonality condition,
, while the
complex orthogonality condition, 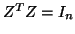 , in (7.91)
would imply
, in (7.91)
would imply 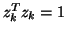 .
Note that for example (7.90), the vector
.
Note that for example (7.90), the vector
![$z=\left[\begin{array}{cc} {\tt i} & 1 \end{array}\right]^T$](img2505.png) spans the one-dimensional eigenspace associated with
spans the one-dimensional eigenspace associated with
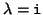 and it satisfies (7.93).
and it satisfies (7.93).





Next: Properties of the Algorithm
Up: Lanczos Method for Complex
Previous: Lanczos Method for Complex
Contents
Index
Susan Blackford
2000-11-20
![]() numbers,
numbers,
![]() is diagonalizable, then
it has an eigendecomposition that reflects the complex symmetry;
see, e.g., [233, Theorem 4.4.13].
More precisely, a complex symmetric matrix
is diagonalizable, then
it has an eigendecomposition that reflects the complex symmetry;
see, e.g., [233, Theorem 4.4.13].
More precisely, a complex symmetric matrix ![]() is diagonalizable
if and only if its eigenvector matrix,
is diagonalizable
if and only if its eigenvector matrix,
![]() , can be chosen such that
, can be chosen such that
![]() , the eigenvector matrix
, the eigenvector matrix
![]() can always be chosen to be unitary:
can always be chosen to be unitary:
![]() with
with