Convergence Properties

In this section, we discuss convergence properties in detail. First the SI is reviewed in the context of the Lanczos algorithm. Next a convergence theory of two-sided algorithms for nonsymmetric eigenvalue problems is outlined with reference to other sections of this work. Finally techniques are reviewed to cope with the unavailability of normalized residuals.

The Ritz values tend to converge first to eigenvalues at the boundary of the convex hull of the spectrum. To compute interior eigenvalues it is often worthwhile to apply a spectral transformation to $A$. The strategy is to accelerate the convergence rate by mapping the desired eigenvalues in the complex plane to the exterior of the transformed spectrum. The standard approach is to apply the Lanczos algorithm to the shifted and inverted matrix

$$C=(A-\sigma I)^{-1}$$ (150)

Eigenvalues in the complex plane nearest the shift $\sigma$ converge first. Note that the LU factorization,

$$A-\sigma I = LU,$$ (151)

can be used to compute both $C q_j = U^{-1}(L^{-1}q)$ and $C^{\ast} p_j = L^{-\ast}(U^{-\ast}p)$ as required in the Lanczos algorithm. See §10.3.

An inherent difficulty of a NHEP is that the known bounds on the distance from $\theta_i^{(j)}$ to an eigenvalue of $A$ are not practical to compute [425,256]. Another complication is that, to be of use, a convergence theory for two-sided algorithms must account for the fact that the left and right Krylov subspaces simultaneously approximate eigenvalues of $A$. These two problems are resolved by bounding the distance, $\Vert F\Vert$, to the nearest matrix, $A-F$, with eigentriplet $(\theta_i^{(j)},x_i^{(j)},y_i^{(j)})$. Eigenvalue sensitivities (condition numbers) are also available. Recall that residual vectors $r_i^{(j)}$ and $s_i^{(j)}$ as defined in (7.40) and (7.41). Next observe that the biorthogonality condition (7.37) implies that $(s_i^{(j)})^{\ast} x_i^{(j)} = (y_i^{(j)})^{\ast} r_i^{(j)} = 0$. Together these relations imply that

$$F = \frac{ r_i^{(j)} (x_i^{(j)})^{\ast} }{ \Vert x_i^{(j)}\V... ...rac{ y_i^{(j)} (s_i^{(j)})^{\ast}}{ \Vert y_i^{(j)}\Vert^2_2 }$$ (152)

is the desired perturbation such that

$$(A-F) x_i^{(j)} = x_i^{(j)} \theta_i^{(j)},$$ (153)

$$(y_i^{(j)})^{\ast} (A-F) = \theta_i^{(j)} (y_i^{(j)})^{\ast},$$ (154)

and $\Vert F\Vert^2_{\rm F} = \Vert r_i^{(j)}\Vert^2_2/ \Vert x_i^{(j)}\Vert^2_2 + \Vert s_i^{(j)}\Vert^2_2 / \Vert y_i^{(j)}\Vert^2_2$. See §7.13 for further discussion on how to derive estimated error bounds on the accuracy of approximate eigenvalues and eigenvectors to the exact eigenvalues and eigenvectors of $A$.

There is a subtle yet critical complication concerning testing the Ritz vectors for convergence. The approximate eigenvectors of the original matrix $A$ are only calculated after the test in step (16) suggests the convergence of Ritz values $\theta^{(j)}_i$ to the desired eigenvalues of $A$. If the Lanczos vectors are stored, then the bases $Q_j$ and $P_j$ are used to get the approximate eigenvectors. If the Lanczos vectors are not stored, then there are two possibilities [93]: one either reruns the three-term recurrences to generate the requested eigenvectors, or applies inverse iteration (see §7.4). The complication is that the decision whether or not to accept a Ritz vector as an approximate eigenvector cannot be based on these unnormalized residuals. After $x_i^{(j)}=Q_jz_i^{(j)}$ and $y_i^{(j)}=P_j w_i^{(j)}$ are computed, it is necessary to compare the normalized residuals

$$\frac{ \Vert r_i^{(j)}\Vert _2 } { \Vert x_i^{(j)} \Vert _2 ... ... \frac{ \Vert s_i^{(j)}\Vert _2 } { \Vert y_i^{(j)} \Vert _2 }$$

to user-specified tolerance. Normalized residuals can be larger in norm than the un-normalized residuals. It may be necessary to reject the computed Ritz vectors, continue the Lanczos algorithm, and then recompute the Ritz vectors. The Ritz vector $x_i^{(j)}$ is rejected if $\Vert Q_j z_i^{(j)}\Vert _2$ is significantly smaller than $\Vert z_i^{(j)}\Vert _2$. There are two common causes for this shrinkage. The first is that due to the loss of biorthogonality, $\theta_i^{(j)}$ is a spurious eigenvalue [93]. This case is addressed either by re-biorthogonalization [105] or by not computing the Ritz vectors that correspond to spurious modes [93].

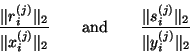
The second common cause of shrinkage is best explained in terms of implementations of the Lanczos algorithm in which $q_j$ and $p_j$ are scaled to have unit Euclidean length [179,354,105]. The inner products

$$\omega_i = \frac{p_j^* q_j}{ \Vert p_j\Vert _2 \Vert q_j\Vert _2}$$

bound the condition numbers of the matrices of Lanczos vectors [354]. In [29] it was shown that

$$\mbox{cond}(Q_j) = \Vert Q_j\Vert _2 \Vert Q^{\dagger}_j\Vert _2 \leq \sum^j_{i=1} \vert \omega_i \vert ^{-1},$$

where $Q^{\dagger}_j$ denotes the generalized inverse of $Q_j$ and the bound also applies to $\mbox{cond}(P_j)$. The right Krylov subspace is nearly invariant if $\Vert r_j\Vert _2$ is tiny relative to the product of the tridiagonal norm (which is easy to estimate) and $\Vert Q_j\Vert _2$. In this scaling, the bound $\Vert Q_j\Vert _2 \leq \sqrt{j}$ simplifies the detection of invariant subspaces.

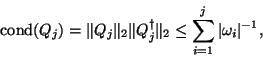
It is common for $\{ \vert \omega_i \vert \}$ to decrease nearly monotonically and by many orders of magnitude over hundreds of Lanczos steps [179,105]. And in this case the unnormalized residuals are poor estimates for Ritz values that do not appear until after $\vert\omega_i\vert$ has decreased by several orders of magnitude. More precisely, for eigenvectors $z_i^{(j)}$ with the special property that $z_i^{(j)}(1:k)$ is negligible, the lower bound

$$\Vert Q_jz_i^{(j)} \Vert _2 \geq \max_{i >k} \vert \omega_i \vert \Vert z_i^{(j)}\Vert _2/\sqrt{j-(k+1)}$$

is likely to be nearly an equality, and if $\max_{i >k} \vert \omega_i \vert$ is extremely small, then forming $Q_jz_i^{(j)}$ is discouraged.