




Next: Software Availability
Up: Convergence Properties
Previous: Convergence Properties
Contents
Index
Multiple eigenvalues can be defective (having only a single eigenvector
and a chain of principal vectors) or derogatory (having several
linearly independent eigenvectors) or both. A normal (or more generally, a
diagonalizable) matrix has only derogatory multiple eigenvalues. The eigenvalue
problem for defective matrices is ill posed. As mentioned
above in the discussion of convergence properties,
perturbation (read approximation) scatters the defective
eigenvalue into a cluster of poorly conditioned eigenvalues.
The Lanczos algorithm has the theoretical advantage that the characteristic
polynomials of the tridiagonal matrices 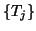 approximate the
minimal polynomial of
approximate the
minimal polynomial of  [234].
This means that in exact arithmetic the Lanczos algorithm computes
a complete chain of principal vectors for a defective
multiple eigenvalue if run for at least as many steps as the length of the
chain.
[234].
This means that in exact arithmetic the Lanczos algorithm computes
a complete chain of principal vectors for a defective
multiple eigenvalue if run for at least as many steps as the length of the
chain.
Susan Blackford
2000-11-20
![]() approximate the
minimal polynomial of
approximate the
minimal polynomial of ![]() [234].
This means that in exact arithmetic the Lanczos algorithm computes
a complete chain of principal vectors for a defective
multiple eigenvalue if run for at least as many steps as the length of the
chain.
[234].
This means that in exact arithmetic the Lanczos algorithm computes
a complete chain of principal vectors for a defective
multiple eigenvalue if run for at least as many steps as the length of the
chain.