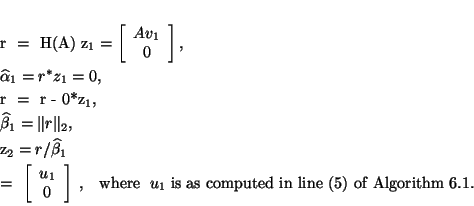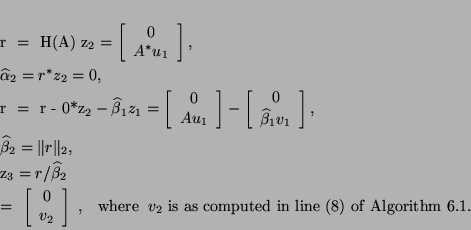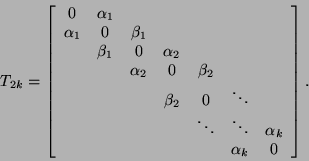Next: Software Availability
Up: Golub-Kahan-Lanczos Method
Previous: Golub-Kahan-Lanczos Bidiagonalization Procedure.
Contents
Index
From equations (6.7), (6.8), and
(6.9), we have
We note that 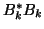 is symmetric and tridiagonal,
since
is symmetric and tridiagonal,
since 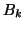 is bidiagonal.
Comparing to equation (4.10), we see that
Algorithm 6.1
computes the same information as
Lanczos (Algorithm 4.6)
applied to the Hermitian matrix
is bidiagonal.
Comparing to equation (4.10), we see that
Algorithm 6.1
computes the same information as
Lanczos (Algorithm 4.6)
applied to the Hermitian matrix 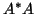 .
Conversely, if we apply Lanczos to
.
Conversely, if we apply Lanczos to 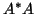 to get a tridiagonal
matrix
to get a tridiagonal
matrix
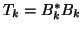 , then
, then 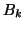 can be obtained by taking the
upper triangular Cholesky factor of
can be obtained by taking the
upper triangular Cholesky factor of 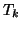 .
.
Similarly, one gets
Again, 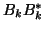 is symmetric and tridiagonal.
So again comparing to equation (4.10), we see that
Algorithm 6.1
computes the same information as
Lanczos (Algorithm 4.6)
applied to the Hermitian matrix
is symmetric and tridiagonal.
So again comparing to equation (4.10), we see that
Algorithm 6.1
computes the same information as
Lanczos (Algorithm 4.6)
applied to the Hermitian matrix 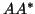 .
Conversely, if we apply Lanczos to
.
Conversely, if we apply Lanczos to 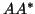 to get a tridiagonal
matrix
to get a tridiagonal
matrix
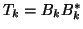 , then
, then 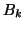 can be obtained by taking the
upper triangular Cholesky factor
can be obtained by taking the
upper triangular Cholesky factor 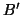 of
of 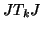 , where
, where 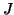 is
the identity matrix with its columns in reverse order
(so that
is
the identity matrix with its columns in reverse order
(so that 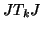 is gotten by reversing the order of the rows
and then the columns of
is gotten by reversing the order of the rows
and then the columns of 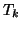 ), and then
), and then 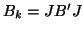 .
.
Finally, suppose one applies Lanczos (Algorithm 4.6)
to 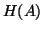 with the special starting vector
with the special starting vector
to generate the Lanczos vectors
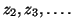 The first step of Algorithm 4.6 yields
The first step of Algorithm 4.6 yields
The next step of Algorithm 4.6 yields
Continuing in this fashion, we see that two steps of
Algorithm 4.6 compute the same information
as one step of Algorithm 6.1:
However, Algorithm 4.6 does twice as many matrix-vectors
multiplications by  and
and 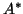 as Algorithm 6.1
(half of them by zero vectors), so that
Algorithm 6.1 will generally use half the time and space.
Conversely, if Lanczos is applied to
as Algorithm 6.1
(half of them by zero vectors), so that
Algorithm 6.1 will generally use half the time and space.
Conversely, if Lanczos is applied to 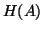 to obtain a
tridiagonal matrix
to obtain a
tridiagonal matrix 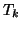 , then
, then 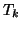 will have zeros on its diagonal,
and the off-diagonal entries will be identical to the nonzero entries
of
will have zeros on its diagonal,
and the off-diagonal entries will be identical to the nonzero entries
of 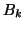 (notation from equation (6.4)):
(notation from equation (6.4)):
Because of these equivalences, all the algorithmic variations
and convergence properties of Lanczos from §4.4 apply to
Algorithm 6.1.





Next: Software Availability
Up: Golub-Kahan-Lanczos Method
Previous: Golub-Kahan-Lanczos Bidiagonalization Procedure.
Contents
Index
Susan Blackford
2000-11-20
![]() with the special starting vector
with the special starting vector